数组问题之《两数之和》以及《三数之和》

Posted 2022-08-06 爱上口袋的天空

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数组问题之《两数之和》以及《三数之和》相关的知识，希望对你有一定的参考价值。

一、简介

        在程序设计中，为了处理方便，常常需要把具有相同类型的若干元素按有序的形式组织起来，这种形式就是数组（Array）。

        数组是程序中最常见、也是最基本的数据结构。在很多算法问题中，都少不了数组的处理和转换。

对数组进行处理需要注意以下特点：

首先，数组会利用索引来记录每个元素在数组中的位置，且在大多数编程语言中，索引是从 0 算起的。我们可以根据数组中的索引，快速访问数组中的元素。事实上，这里的索引其实就是内存地址
   其次，作为线性表的实现方式之一，数组中的元素在内存中是连续存储的，且每个元素占用相同大小的内存

二、案例之两数之和

1、题目说明

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
2、方法一：暴力法

看到一道算法题，首先考虑暴力解法，再进行优化。暴力法其实非常简单：把所有数、两两组合在一起，计算它们的和，如果是target，就输出。

代码实现如下：
public int[] twoSum(int[] nums, int target) 
    for( int i = 0; i < nums.length; i++ )
        for( int j = i + 1; j < nums.length; j++ )
            if( nums[i] + nums[j] == target )
                return new int[] i, j;
        



    
    throw new IllegalArgumentException("No two sum solution");
3、方法二：两遍哈希表

        为了对运行时间复杂度进行优化，我们需要一种更有效的方法来检查数组中是否存在目标元素。如果存在，我们需要找出它的索引。这可以使用哈希表来实现。

        具体实现方法，最简单就是使用两次迭代。

        在第一次迭代中，我们将每个元素的值和它的索引添加到表中；然后，在第二次迭代中，我们将检查每个元素所对应的目标元素 (target-nums[i]) 是否存在于表中。

代码如下：
public int[] twoSum(int nums[], int target) 
        Map<Integer, Integer> map = new HashMap<>();

        // 遍历数组，全部保存到 hashmap中
        for(int i = 0; i < nums.length; i++)
            map.put(nums[i], i);
        

        // 遍历数组，挨个查找对应的“那个数”在不在map中
        for( int i = 0; i < nums.length; i++ )
            int thatNum = target - nums[i];
            if( map.containsKey(thatNum) && map.get(thatNum) != i )
                return new int[] i, map.get(thatNum);
        
        throw new IllegalArgumentException("No two sum solution");
复杂度分析：

时间复杂度：O(N)，我们把包含有 N 个元素的列表遍历两次。由于哈希表将查找时间缩短到 O(1)，所以时间复杂度为 O(N)。
空间复杂度：O(N)，所需的额外空间取决于哈希表中存储的元素数量，该表中存储了 N 个元素。

3、方法三：一遍哈希表

在上述算法中，我们对哈希表进行了两次扫描，这其实是不必要的。在进行迭代并将元素插入到表中的同时，我们可以直接检查表中是否已经存在当前元素所对应的目标元素。如果它存在，那我们已经找到了对应解，并立即将其返回。这样，只需要扫描一次哈希表，就可以完成算法了。
public int[] twoSum(int nums[], int target) 
        Map<Integer, Integer> map = new HashMap<>();

        for( int i = 0; i < nums.length; i++ )
            int thatNum = target - nums[i];
            if( map.containsKey(thatNum) && map.get(thatNum) != i )
                return new int[] map.get(thatNum), i;
            map.put(nums[i], i);
        
        throw new IllegalArgumentException("No two sum solution");
复杂度分析：

时间复杂度：O(N)，我们只遍历了包含有 N 个元素的列表一次。在表中进行的每次查找只花费 O(1) 的时间。其实这个过程中，我们也借鉴了动态规划的思想、把子问题解保存起来，后面用到就直接查询。
空间复杂度：O(N)，所需的额外空间取决于哈希表中存储的元素数量，该表最多需要存储 N 个元素。

三、三数之和

1、简介

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4]，
满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]
2、分析

        这个问题比起两数之和来，显然要复杂了一些，而且由于结果可能有多种情况，还要考虑去重，整体难度提升了不少。

        最后的返回，就不再是一个简单的数组了，而是“数组的数组”，每一组解都是一个数组，最终有多组解都要返回。

3、方法一：暴力法

        最简单的办法，当然还是暴力法。基本思路是，每个人都先去找到另一个人，然后再一起逐个去找第三个人。

很容易想到，实现起来就是三重循环：这个时间复杂度是 O(n^3)。
 public List<List<Integer>> threeSum(int[] nums) 
        int n = nums.length;
        List<List<Integer>> resultList = new ArrayList<>();
        // 三重循环，遍历所有的三数组合
        for( int i = 0; i < n - 2; i++ )
            for( int j = i + 1; j < n - 1; j++ )
                for( int k = j + 1; k < n; k++ )
                    if( nums[i] + nums[j] + nums[k] == 0 )
                        resultList.add(
                                Arrays.asList(nums[i], nums[j], nums[k]));
                    
                
            
        
        return resultList;
    
运行一下，我们会发现，这个结果其实是不正确的没有去重，同样的三元组在结果中无法排除。比如-1，0，1会出现两次。而且时间复杂度非常高，是N^3。

所以接下来，我们就要做一些改进，试图降低时间复杂度，而且解决去重问题

4、暴力法的改进：结果去重

要做去重，自然首先想到的，就是把结果保存到一张hash表里。仿照两数之和，直接存到HashMap里查找，代码如下：
public List<List<Integer>> threeSum(int[] nums) 
        int n = nums.length;
        List<List<Integer>> result = new ArrayList<>();

        Map<Integer, List<Integer>> hashMap = new HashMap<>();

        // 遍历数组，寻找每个元素的thatNum
        for( int i = 0; i < n; i++ )
            int thatNum = 0 - nums[i];

            if( hashMap.containsKey(thatNum) )
                List<Integer> tempList = new ArrayList<>(
                        hashMap.get(thatNum));
                tempList.add(nums[i]);
                result.add(tempList);
                continue;
            
            for( int j = 0; j < i; j++ )
                int newKey = nums[i] + nums[j];
                if( ! hashMap.containsKey(newKey) )
                    List<Integer> tempList = new ArrayList<>();
                    tempList.add(nums[j]);
                    tempList.add(nums[i]);
                    hashMap.put( newKey, tempList );
                
            
        
        return result;
    
        时间复杂度降为N^2，空间复杂度O(N)。但是，我们加一个输入[0,0,0,0]，会发现结果不正确。因为尽管通过HashMap存储可以去掉相同二元组的计算结果的值，但没有去掉重复的输出（三元组）。这就导致，0对应在HashMap中有一个值（0，List（0，0）），第三个0来了会输出一次，第四个0来了又会输出一次。如果希望解决这个问题，那就需要继续加入其它的判断来做去重，整个代码复杂度会变得更高。

5、方法二：双指针法

暴力法搜索时间复杂度为O(N^3)，要进行优化，可通过双指针动态消去无效解来提高效率。

双指针的思路，又分为左右指针和快慢指针两种。

        我们这里用的是左右指针。左右指针，其实借鉴的就是分治的思想，简单来说，就是在数组头尾各放置一个指针，先让头部的指针（左指针）右移，移不动的时候，再让尾部的指针（右指针）左移：最终两个指针相遇，那么搜索就结束了。

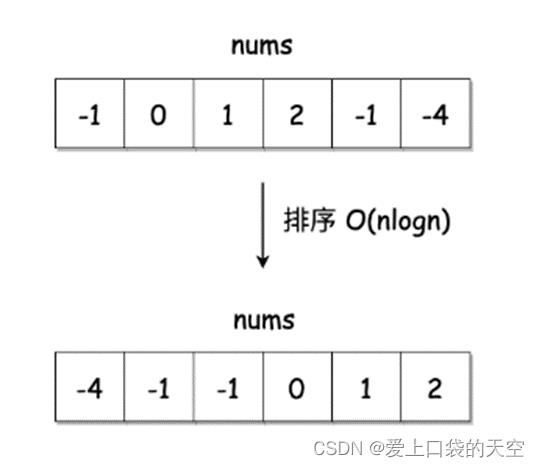
（1）双指针法铺垫：先将给定 nums 排序，复杂度为 O(NlogN)。

        首先，我们可以想到，数字求和，其实跟每个数的大小是有关系的，如果能先将数组排序，那后面肯定会容易很多。

        之前我们搜索数组，时间复杂度至少都为O(N^2)，而如果用快排或者归并，排序的复杂度，是 O(NlogN)，最多也是O(N^2)。所以增加一步排序，不会导致整体时间复杂度上升。

下面我们通过图解，来看一下具体的操作过程。

（2）初始状态，定义左右指针L和R，并以指针i遍历数组元素。

固定 3 个指针中最左（最小）数字的指针 i，双指针 L，R 分设在数组索引 (i, len(nums)) 两端，所以初始值，i=0；L=i+1；R=nums.length-1
通过L、R双指针交替向中间移动，记录对于每个固定指针 i 的所有满足 nums[i] + nums[L] + nums[R] == 0 的 L,R 组合。

两个基本原则：

当 nums[i] > 0 时直接break跳出：因为 nums[R] >= nums[L] >= nums[i] > 0，即 3 个数字都大于 0 ，在此固定指针 i 之后不可能再找到结果了。
当 i > 0且nums[i] == nums[i - 1]时，即遇到重复元素时，跳过此元素nums[i]：因为已经将 nums[i - 1] 的所有组合加入到结果中，本次双指针搜索只会得到重复组合。

（3）固定i，判断sum，然后移动左右指针L和R。

        L，R 分设在数组索引 (i, len(nums)) 两端，当L < R时循环计算当前三数之和：

        sum = nums[i] + nums[L] + nums[R]

并按照以下规则执行双指针移动：

当sum < 0时，L ++并跳过所有重复的nums[L]；

由于sum<0，L一直右移，直到跟R重合。如果依然没有结果，那么i++，换下一个数考虑。

换下一个数，i++，继续移动双指针：

初始同样还是L=i+1，R=nums.length-1。同样，继续判断sum。

找到一组解之后，继续移动L和R，判断sum，如果小于0就右移L，如果大于0就左移R：

找到一组解[-1,-1,2]，保存，并继续右移L。判断sum，如果这时sum=-1+0+2>0，（R还没变，还是5），那么就让L停下，开始左移R。

一直移动，又找到一组解

如果又找到sum=0的一组解，把当前的[-1,0,1]也保存到结果数组。继续右移L。

如果L和R相遇或者L>R，代表当前i已经排查完毕，i++；如果i指向的数跟i-1一样，那么直接继续i++，考察下一个数；

这时i=3，类似地，当sum > 0时，R左移R -= 1，并跳过所有重复的nums[R]；

L和R相遇，结束当前查找，i++。

当 nums[i] > 0 时直接break跳出：过程结束。

所以，最终的结果，就是[-1,-1,2],[-1,0,1]。

代码如下：
public List<List<Integer>> threeSum(int[] nums)
        int n = nums.length;
        List<List<Integer>> result = new ArrayList<>();

        // 先对数组进行排序
        Arrays.sort(nums);

        for( int i = 0; i < n; i++ )
            if( nums[i] > 0 )
                break;
            if( i > 0 && nums[i] == nums[i-1] )
                continue;
            // 定义左右指针（索引位置）
            int lp = i + 1;
            int rp = n - 1;
            // 只要左右不重叠，就继续移动指针
            while( lp < rp )
                int sum = nums[i] + nums[lp] + nums[rp];
                if( sum == 0 )
                    result.add(Arrays.asList(nums[i], nums[lp], nums[rp]));
                    lp ++;
                    rp --;
                    while( lp < rp && nums[lp] == nums[lp - 1] )
                        lp ++;
                    while( lp < rp && nums[rp] == nums[rp + 1] )
                        rp --;
                
                else if( sum < 0 )
                    lp ++;
                else
                    rp --;
            
        
        return result;
    
复杂度分析：

时间复杂度 O(N^2)：其中固定指针k循环复杂度 O(N)，双指针 i，j 复杂度 O(N)。比暴力法的O(n^3)，显然有了很大的改善。
空间复杂度 O(1)：指针使用常数大小的额外空间。

尽管时间复杂度依然为O(n^2)，但是过程中避免了复杂的数据结构，空间复杂度仅为常数级O(1)，可以说，双指针法是一种很巧妙、很优雅的算法设计。