哈希表—哈希函数的设计

Posted 2023-03-19

参考技术A 上一篇文章中，我们举了 身份证号为关键字 的例子。这里，我们假设真的有一个无限大的空间，那么，可以直接将身份证号作为索引吗？

显然不合适。因为，并不是所有的身份证号都是18位的，对于那些位数在17位以下的，就太浪费这个大空间了。

设计哈希函数的原则是，将我们所关心的键通过哈希函数求出索引， “键”通过哈希函数得到的“索引”分布越均匀越好 (实际上，实现起来非常困难)

那么，对于像身份证号这样的大整数为关键字时，该怎么计算对应的索引呢？

或者像复合类、字符串、浮点数这样类型的关键字，该如何计算它们对应的索引呢？

对于哈希函数来说，我们只能将整型数据作为关键字来求解索引。所以，不管什么类型的关键字，我们应该先将其转化为整型类型的数据。

按照这个思路，以下介绍几种最简单、最基础、最一般、最通用的哈希函数

小范围正整数直接使用

例如，上一篇讲的ASCII值作为关键字

再例如，一个班有30个学生，1—30表示每位学生对应的学号，并作为关键字

像这样的小范围正整数，可以直接将关键字作为索引，存储到数组中去

小范围负整数进行偏移

例如，-100～100的数作为关键字，这时可以每个数都加上100，变为0～200的正整数

这样，就可以将关键字直接作为索引存储到数组中去

大整数取模

例如，身份证号作为关键字，412637199707096354

取后四位(6354)。也就是，mod 10000

假如，取后六位(096354)。即，mod 100 0000 这样，会 分布不均匀

对于身份证号来说，后六位的前两位(09)代表着日期数，也就是1～31的数字。那么，这个六位数不会达到32 0000这么大，中国这么多人口，显然这个数字是不够的，这也就造成了索引分布不均匀

这也就体现了哈希函数的复杂性，也说明了具体问题要具体分析。

上面的取模方式还有一个问题，没有 有效利用所有信息。 我们这样取模，只是利用了关键字的一部分，也就是不管这个人是哪个地区哪个年份出生的，都有可能存储到一个地址中去，这样会增加哈希冲突的概率。那么，该如何解决这个问题呢？

一个简单的解决办法： 模一个素数

为什么要模一个素数呢？简单举个例子

显然，模一个素数，结果会分布的更均匀，哈希冲突的概率也会变小。我们该如何选择这个素数呢？相关的领域专家已经为我们研究出了答案。

假如，需要存储的数在2^5～2^6之间，模上53就可以了。

注：这个表并不是唯一的，一个区间内可以有多个素数

将浮点型解析成大整型，之后再相应取模(如上)

先看一个例子

把一个整数用科学计数法来表示，同样，字符串也可以类似表示。将这个字符串看成26进制，是因为有26个小写字母，如果字符串中有大写字母或者标点符号，那么看成26进制显然是不够的，可以看成是100进制或者256进制等。显然，这个进制是用户可以自己选择的，我们用 B 来表示这个进制

每一个小写字母对应一个数字，这样我们把字符串也转化成了大整型，之后就可以利用上面取模的方式计算哈希值了。

这样就可以计算出字符串的哈希值了。当B是一个比较大的数或者字符串比较长时，求B的k次方是比较浪费时间的，所以我们可以优化这个表达式

这样就省去了求次方运算。但是，还有可能会出现整型溢出的情况，当B是一个很大的数字或者字符串很长的时候，我们可以再次优化这个表达式

这样，每退出一个小括号，数字都会变成比M先得数字，就不会出现溢出情况了

假如我们自己定义一个类，日期类

Date：year，month，day

为这个Date类设计哈希函数，可以像字符串那样，将类的属性值看着是一个字符

这样，就求出了复合类的哈希值。

一致性： 当关键字相同时，经过哈希函数求出的哈希值也是相同的。

反过来是不成立的，即当哈希值相同时关键字不一定相同。哈希值相同，取模后得到的索引也相同，即不同的关键字对应的存储位置相同，这也就是所谓的哈希冲突。

高效性： 我们设计哈希函数就是为了高效存储数据，如果哈希函数的设计就消耗过多性能，那么就得不偿失了

均匀性： 通过哈希函数求出的索引必须是分布均匀的。

以上，就是转化为整型求哈希函数。但是， 这并不是求哈希函数唯一的方法 。

算法初级面试题05——哈希函数/表生成多个哈希函数哈希扩容利用哈希分流找出大文件的重复内容设计RandomPool结构布隆过滤器一致性哈希并查集岛问题

今天主要讨论：哈希函数、哈希表、布隆过滤器、一致性哈希、并查集的介绍和应用。

 

题目一

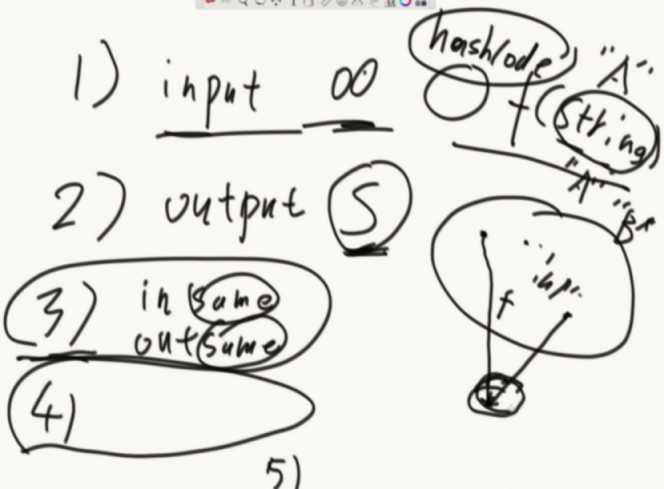
认识哈希函数和哈希表

1、输入无限大

2、输出有限的S集合

3、输入什么就输出什么

4、会发生哈希碰撞

5、会均匀分布，哈希函数的离散性，打乱输入规律

 

 

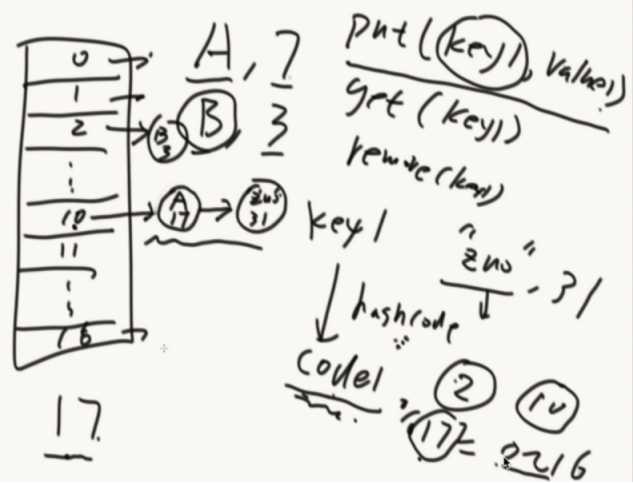
public class Code_01_HashMap {

    public static void main(String[] args) {
        HashMap<String, String> map = new HashMap<>();
        map.put("zuo", "31");

        System.out.println(map.containsKey("zuo"));
        System.out.println(map.containsKey("chengyun"));
        System.out.println("=========================");

        System.out.println(map.get("zuo"));
        System.out.println(map.get("chengyun"));
        System.out.println("=========================");

        System.out.println(map.isEmpty());
        System.out.println(map.size());
        System.out.println("=========================");

        System.out.println(map.remove("zuo"));
        System.out.println(map.containsKey("zuo"));
        System.out.println(map.get("zuo"));
        System.out.println(map.isEmpty());
        System.out.println(map.size());
        System.out.println("=========================");

        map.put("zuo", "31");
        System.out.println(map.get("zuo"));
        map.put("zuo", "32");
        System.out.println(map.get("zuo"));
        System.out.println("=========================");

        map.put("zuo", "31");
        map.put("cheng", "32");
        map.put("yun", "33");

        for (String key : map.keySet()) {
            System.out.println(key);
        }
        System.out.println("=========================");

        for (String values : map.values()) {
            System.out.println(values);
        }
        System.out.println("=========================");

        map.clear();
        map.put("A", "1");
        map.put("B", "2");
        map.put("C", "3");
        map.put("D", "1");
        map.put("E", "2");
        map.put("F", "3");
        map.put("G", "1");
        map.put("H", "2");
        map.put("I", "3");
        for (Entry<String, String> entry : map.entrySet()) {
            String key = entry.getKey();
            String value = entry.getValue();
            System.out.println(key + "," + value);
        }
        System.out.println("=========================");

        // you can not remove item in map when you use the iterator of map
//         for(Entry<String,String> entry : map.entrySet()){
//             if(!entry.getValue().equals("1")){
//                 map.remove(entry.getKey());
//             }
//         }

        // if you want to remove items, collect them first, then remove them by
        // this way.
        List<String> removeKeys = new ArrayList<String>();
        for (Entry<String, String> entry : map.entrySet()) {
            if (!entry.getValue().equals("1")) {
                removeKeys.add(entry.getKey());
            }
        }
        for (String removeKey : removeKeys) {
            map.remove(removeKey);
        }
        for (Entry<String, String> entry : map.entrySet()) {
            String key = entry.getKey();
            String value = entry.getValue();
            System.out.println(key + "," + value);
        }
        System.out.println("=========================");
    }
}

 

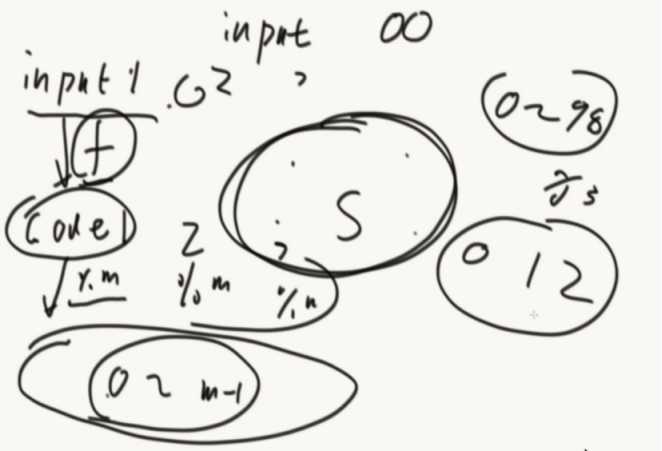
推论：如果结果都%一个M，那么0~m-1这个区域也是均匀分布的。

 

怎么拥有1000个相对独立的哈希函数。

把h计算出的16位数，分成高8位h1和低8位h2，然后h1 + 1*h2 =h3

生成新的哈希函数。（每个位置都是独立的，都是通过hash函数不断异或处理计算出来的）

 

 

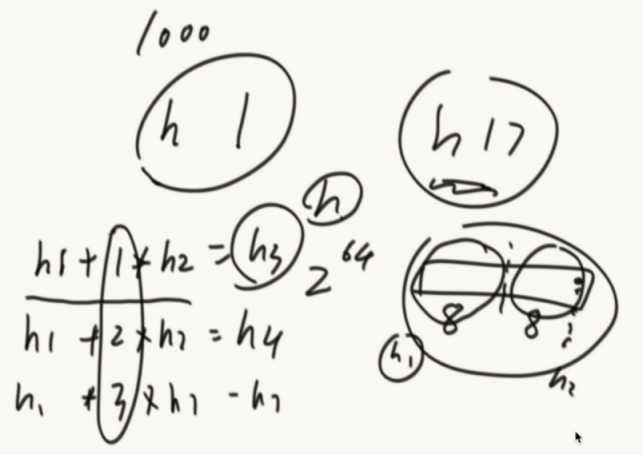
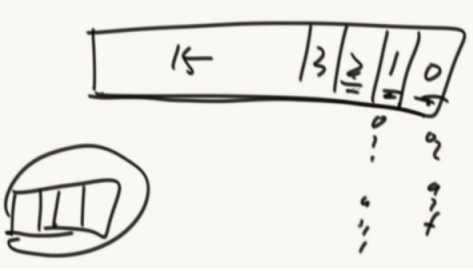
哈希表经典结构：

 

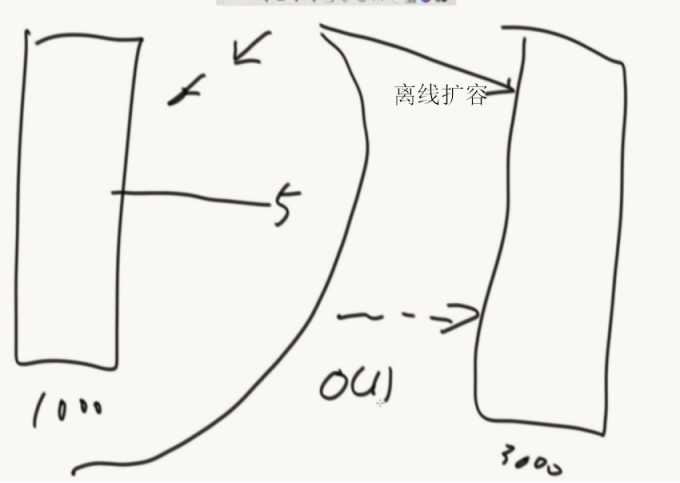
哈希扩容：

扩容要把以前的元素拿出来，重新计算然后放入新的空间，为了不影响效率也可以使用离线时间进行扩容（push就同时两个都push，get的话先从原来的地方拿）。

增删改查，全为o(1)

 

 

 

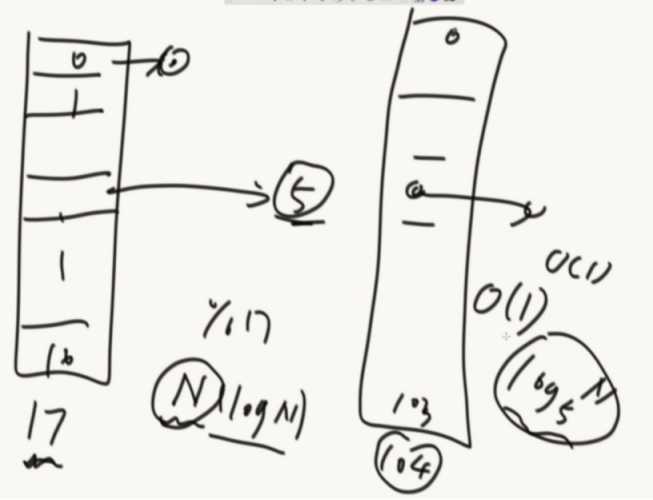
JVM里面的实现：

利用了平衡搜索二叉树

数组+红黑色的哈希表，使用了TreeMap结构

 

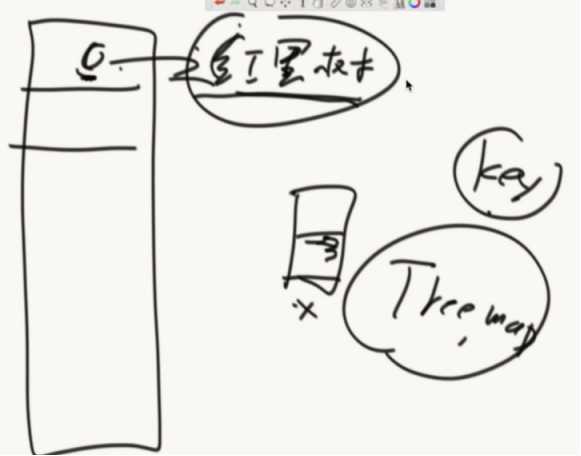
哈希表多有用？引入一道题目：

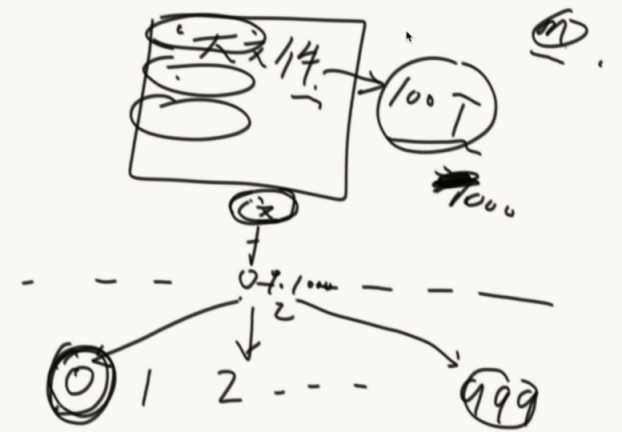
有一个大文件（100T），每行是一个字符串，想把大文件里面重复的内容打印出来

 

问面试官：你给我多少台机器？1000台机器

给机器编号0~999

然后从100T里面开始读文本，然后把文本按照hash函数算出hashcode再%上1000，如果是0就扔到0机器...，这样就把大文件分到1000台机器上。

根据hash的性质，相同的文本会来到同一台机器上。然后再单台机器上统计哪些重复的。

如果还太大的话，可以再机器里面再分文件。（hash函数做分流）

 

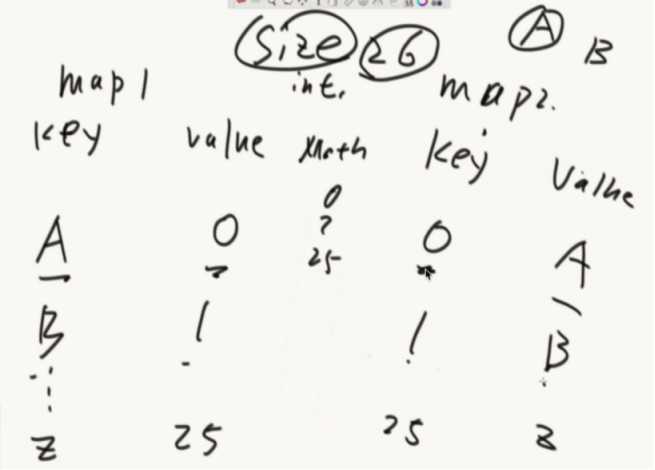
题目二

设计RandomPool结构

【题目】 设计一种结构，在该结构中有如下三个功能：insert(key)：将某个key加入到该结构，做到不重复加入。delete(key)：将原本在结构中的某个key移除。 getRandom()：等概率随机返回结构中的任何一个key。

【要求】 Insert、delete和getRandom方法的时间复杂度都是 O(1)

 

做法：准备两张hash表和整形变量size，每加入一个数就分别存在两个hash表中，利用math.random随机从第二个hash表中返回一个数。

 

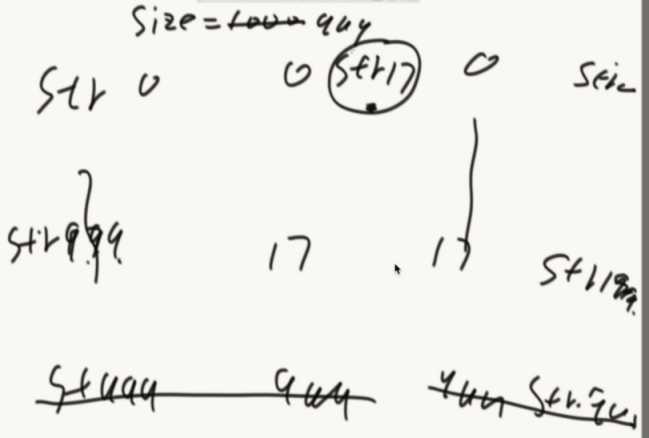
怎么解决删的问题？

拿最后一个值去填这个洞，然后删了最后一个。size再减一。

 

public class Code_02_RandomPool {

    public static class Pool<K> {
        private HashMap<K, Integer> keyIndexMap;
        private HashMap<Integer, K> indexKeyMap;
        private int size;

        public Pool() {
            this.keyIndexMap = new HashMap<K, Integer>();
            this.indexKeyMap = new HashMap<Integer, K>();
            this.size = 0;
        }

        public void insert(K key) {
            if (!this.keyIndexMap.containsKey(key)) {
                this.keyIndexMap.put(key, this.size);
                this.indexKeyMap.put(this.size++, key);
            }
        }

        public void delete(K key) {
            if (this.keyIndexMap.containsKey(key)) {
                int deleteIndex = this.keyIndexMap.get(key);
                int lastIndex = --this.size;
                K lastKey = this.indexKeyMap.get(lastIndex);
                this.keyIndexMap.put(lastKey, deleteIndex);
                this.indexKeyMap.put(deleteIndex, lastKey);
                this.keyIndexMap.remove(key);
                this.indexKeyMap.remove(lastIndex);
            }
        }

        public K getRandom() {
            if (this.size == 0) {
                return null;
            }
            int randomIndex = (int) (Math.random() * this.size); // 0 ~ size -1
            return this.indexKeyMap.get(randomIndex);
        }

    }

    public static void main(String[] args) {
        Pool<String> pool = new Pool<String>();
        pool.insert("zuo");
        pool.insert("cheng");
        pool.insert("yun");
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
        System.out.println(pool.getRandom());
    }
}

 

题目三

认识布隆过滤器（面试搜索相关的公司几乎都会问到）

就是一个某种类型的集合，不过会有失误率。

 

 

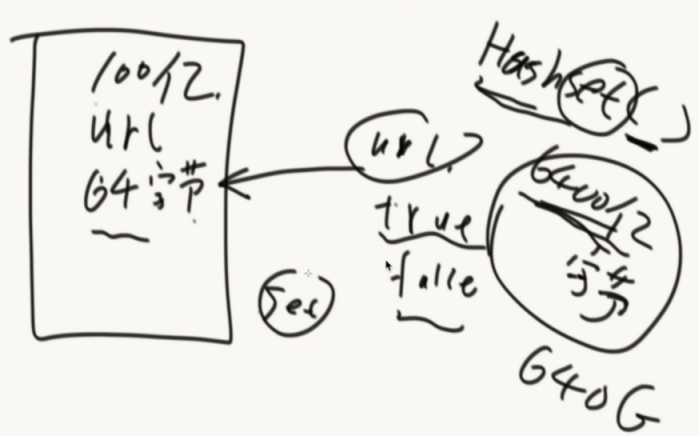
实现0~m-1比特的数组（处理黑名单问题）

原本的数 | 1 << 16  就可以把32字节里面的第16位改为1

 

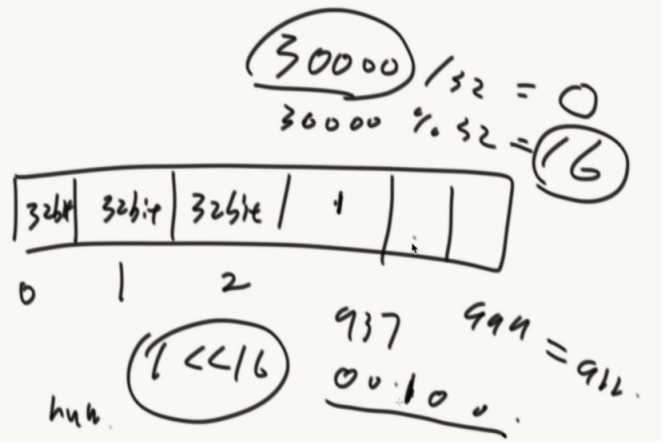
public class c05_03BloemFilter {

    //实现0~m-1比特的数组
    public static void main(String[] args) {
        //int 4个字节 32个比特
        int[] arr = new int[1000];//4*8*1000 = 32000;

        //数量不够可以使用二维数组实现
        long[][] map = new long[1000][1000];

        int index = 30000;//想把第30000位置描黑

        int intIndex = index / 4 / 8;//查看这个bit来自哪个整数位置

        int bitIndex = index % 32;//在定位来自这个整数的哪个bit位

        arr[intIndex] = arr[intIndex] | (1 << bitIndex);
    }

}

 

一个URL经过K个hash函数，计算出K个位置都描黑。（这个URL就进入到布隆过滤器当中了）

接下来每个URL都这样计算加入到bit类型的数组里面。（数组要够大）

怎么查？

这个URL经过K个hash函数，算出来K个位置，如果K个位置都是黑的就说这个URL在黑名单中，如果有一个不是黑的就不在黑名单里

 

数组空间越大，失误率会降低，空间多大和样本量、预计失误率有关系

 

 

数组的大小M（bit）有一个公式计算。22.3G

 

 

确定hash函数的个数K，最后P会在确定了M和K后计算出来

 

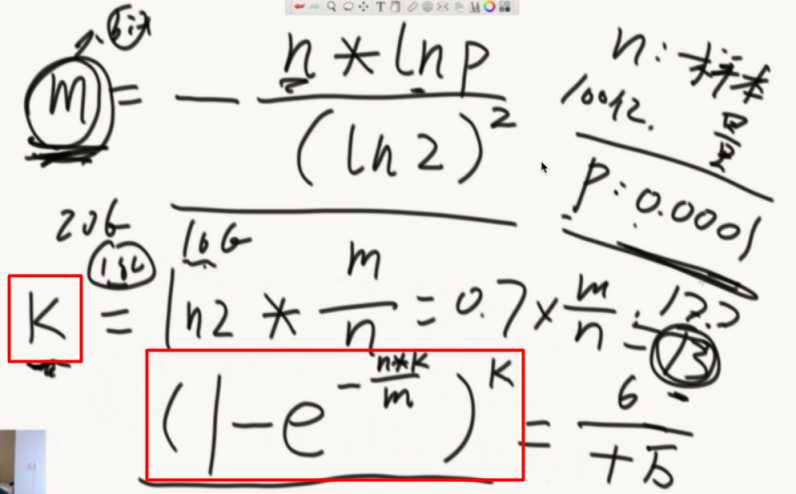
如果面试官感觉经典结构太费，就问面试官允不允许有失误率，失误率是多少，允许就讲布隆过滤器的原理，URL经过K个hash然后描黑数组，检查URL的时候通过K个hash来检查。都黑就在，否则就不在。

 

数组开多大，由样本量、失误率，计算出bit后还要除以8才是字节数。

如果计算出16G，面试官给出20G空间就适当调整大到18G

接着就计算hash的个数K，向上取整。

最后再计算下失误率。

 

题目四

认识一致性哈希（服务器设计）

服务器经典结构怎么做到负载均衡，前端通过同一份hash函数，计算出hashcode再%3，得到0/1/2然后存在不同的服务器中。由于hash函数的性质，这个服务器巨均衡。

 

 

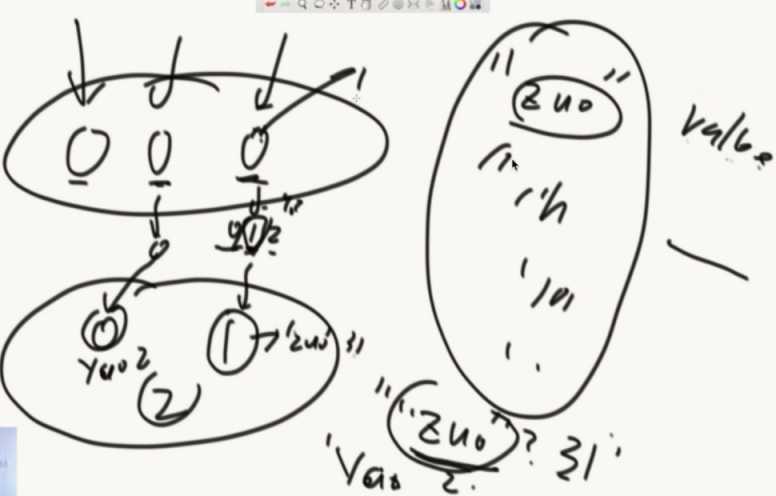
当想加减机器的时候，这个结构就干了。和hash表扩容一样。所有的数据归属全变了。（代价很大）

引入一致性哈希结构。

把hash函数的返回值想象成一个环。再把机器M1/M2/M3的IP经过hash计算放在环里面，接着要进入一个数据”zuo”就入环，顺时针找到最近的机器存进去。

 

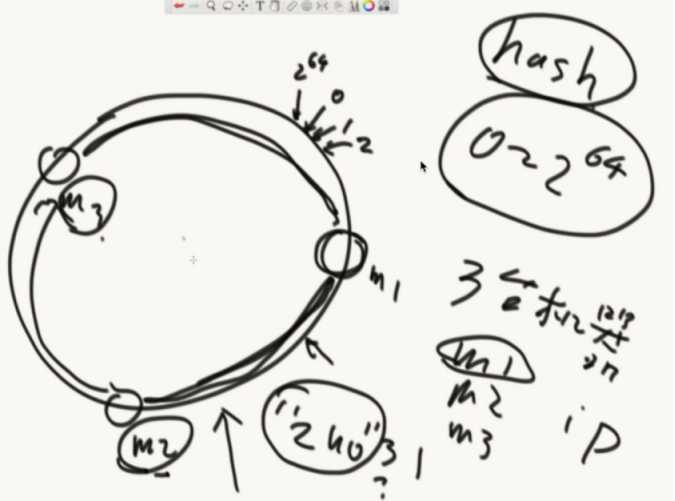
怎么实现？

把机器的hash值排序后做成数组，存在每个前端服务器中。

在数据访问的时候，通过计算hash值，二分的方式查询机器数组，查询出最近的大于等于机器。

 

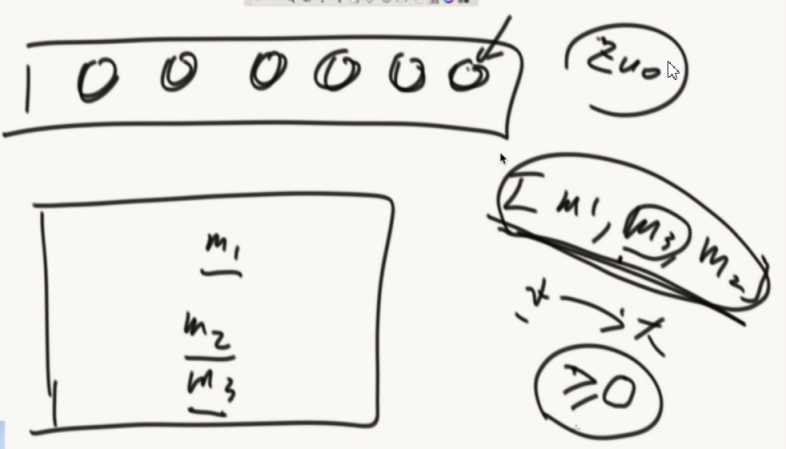
前端服务器二分的查找服务器过程，就是一个顺时针找最近服务器的过程。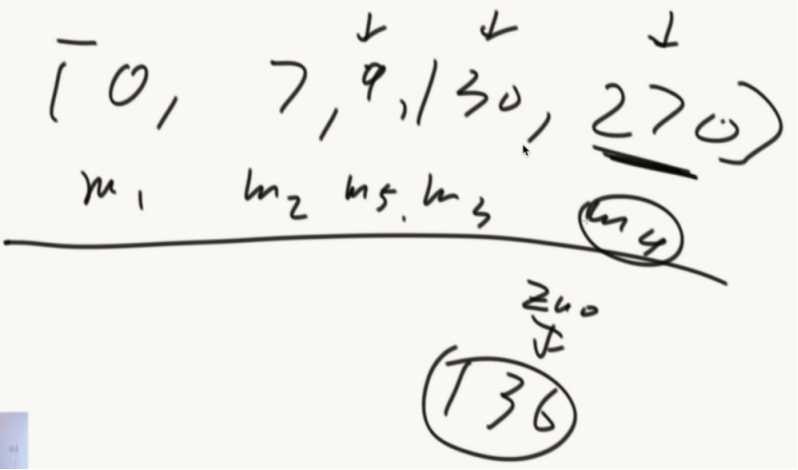

 

 

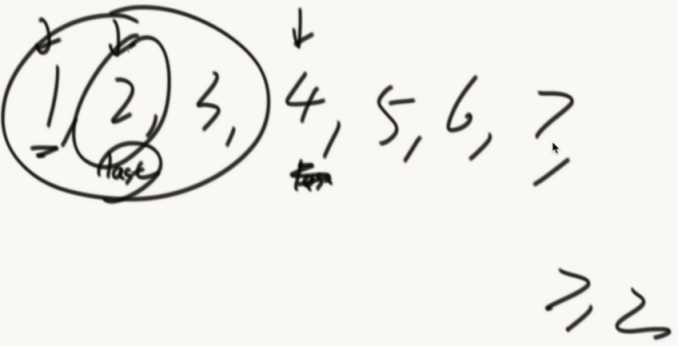
新增一个机器的情况：

M4通过IP计算出位置，数据迁移只需要一小部分。新增和删除都只需要一小部分数据。

 

 

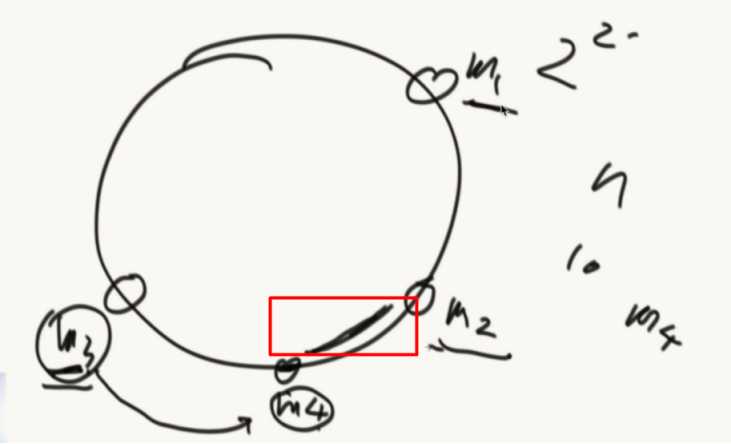
在机器数量小的时候，不能确保机器均匀分布。

 

什么技术可以解决这个问题？

虚拟节点技术。

给M1/M2/M3,1000个虚拟节点。

准备一张路由表，虚拟节点可以找到自己对应的节点。

把3000个节点。存入环中，那么机器们负责的数据就差不多一样了

 

新增了M4之后，也加入1000个节点，把相应的数据进行调整。

 

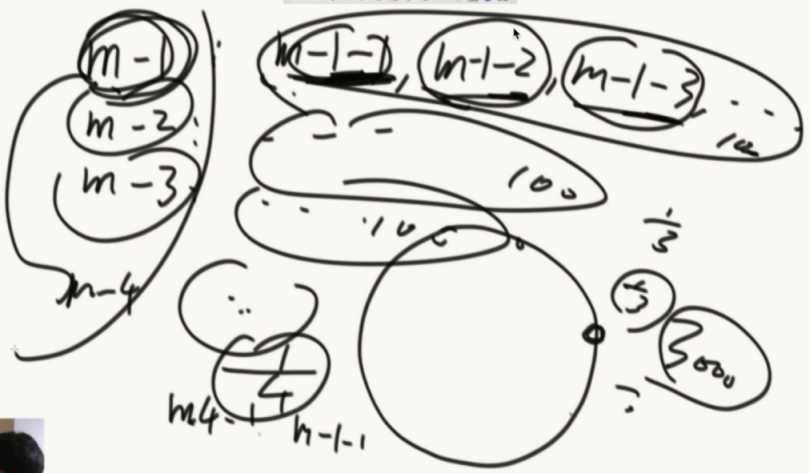
几乎所有需要集群化都进行了一致性哈希的改造。

 

题目五

岛问题

一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右四个位置相连，如果有一片1连在一起，这个部分叫做一个岛，求一个矩阵中有多少个岛？

 

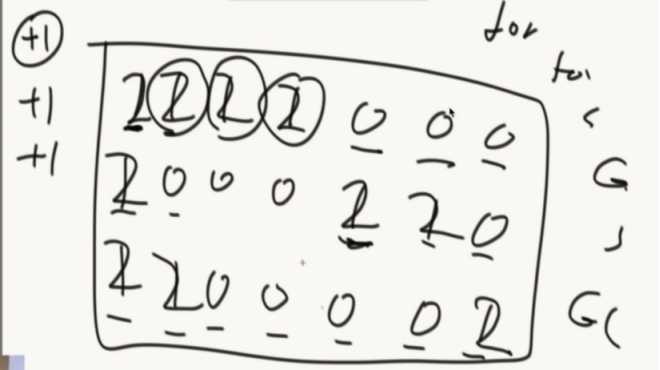
举例：

0 0 1 0 1 0

1 1 1 0 1 0

1 0 0 1 0 0

0 0 0 0 0 0

这个矩阵中有三个岛。

如果矩阵巨大无比，但是有几个CPU，设计一个多任务并行的算法。

经典解法：

遍历矩阵，碰到1就启动感染函数（递归改变数值的函数），把1周围的变为2，岛屿+1，直到遍历结束。

 

 

public class Code_03_Islands {

    public static int countIslands(int[][] m) {
        if (m == null || m[0] == null) {
            return 0;
        }
        int N = m.length;
        int M = m[0].length;
        int res = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if (m[i][j] == 1) {
                    res++;
                    infect(m, i, j, N, M);
                }
            }
        }
        return res;
    }

    public static void infect(int[][] m, int i, int j, int N, int M) {
        if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) {
            return;
        }
        m[i][j] = 2;
        infect(m, i + 1, j, N, M);
        infect(m, i - 1, j, N, M);
        infect(m, i, j + 1, N, M);
        infect(m, i, j - 1, N, M);
    }

    public static void main(String[] args) {
        int[][] m1 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, 
                        { 0, 1, 1, 1, 0, 1, 1, 1, 0 }, 
                        { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
                        { 0, 1, 1, 0, 0, 0, 0, 0, 0 }, 
                        { 0, 0, 0, 0, 0, 1, 1, 0, 0 }, 
                        { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                        { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
        System.out.println(countIslands(m1));

        int[][] m2 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, 
                        { 0, 1, 1, 1, 1, 1, 1, 1, 0 }, 
                        { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
                        { 0, 1, 1, 0, 0, 0, 1, 1, 0 }, 
                        { 0, 0, 0, 0, 0, 1, 1, 0, 0 }, 
                        { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                        { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
        System.out.println(countIslands(m2));

    }

}

多任务解题思路：

要解决合并岛的问题

 

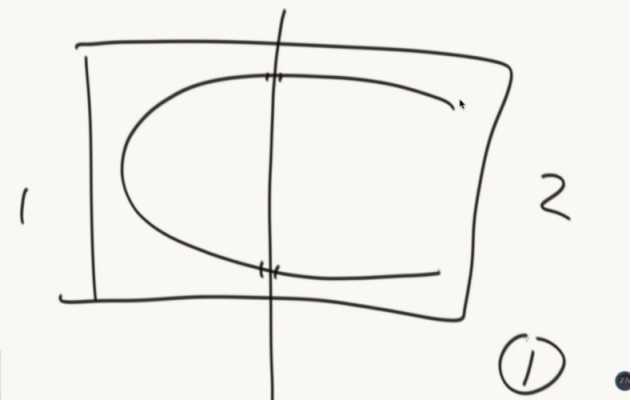
把岛的数量和边界信息存储起来。

 

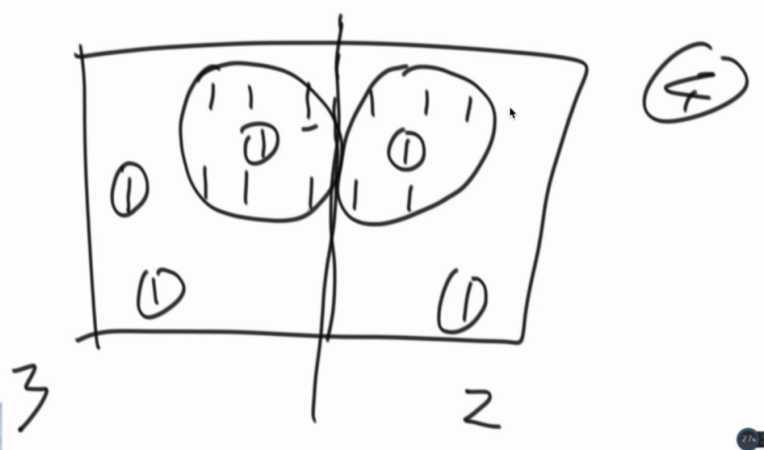
边界信息要如何合并：

标记感染中心。（并查集应用）

看边界A和边界C是否合并过，没有就合并（指向同一个标记），岛数量减一。

如何一路下去会碰到B和C，再次检查，合并，岛减一。

 

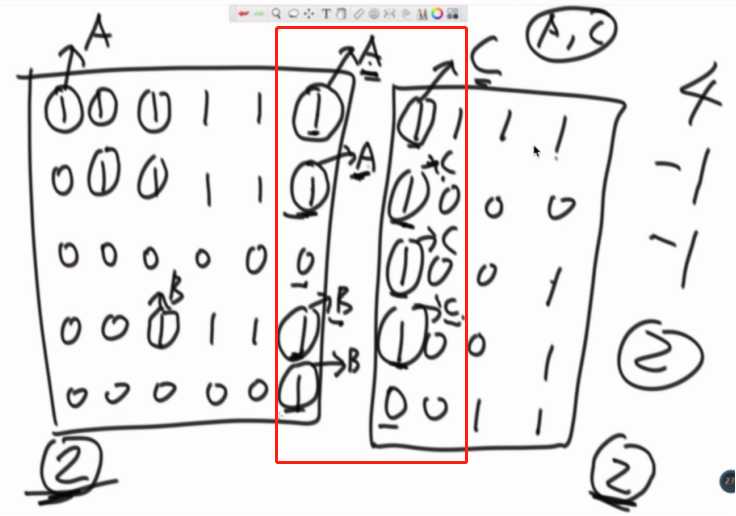
连成一片的这个概念，用并查集这个结构能非常好做，在结构上，怎么避免已经合完的部分，不重复减岛这个问题，用并查集来解决。

 

多边界的话就是收集的信息多一点而已，合并思路是一样的。

可以把边界信息都扔在一个并查集里面合并。（和面试官吹水的部分）

 

可以分成多个部分给多个CPU操作，得到结果后再合并最后的结果。（看具体情况，可使用二分法）

 

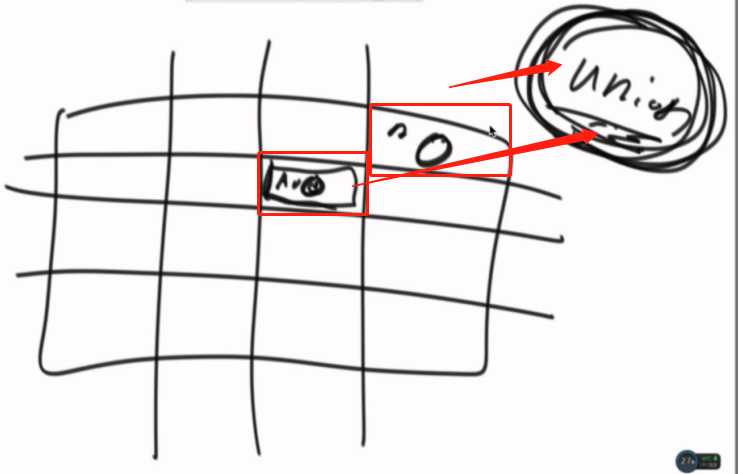
题目六

认识并查集结构（用之前给所有的数据）

1、非常快的检查两个元素是否在同一个集合。isSameSet

2、两个元素各种所在的集合，合并在一起。Union(元素,元素)

 

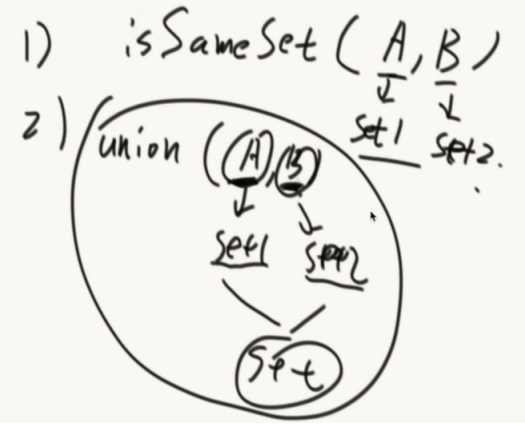
使用list的话合并快，查询是否在同一个集合慢。

使用set的话查询快，合并慢。

 

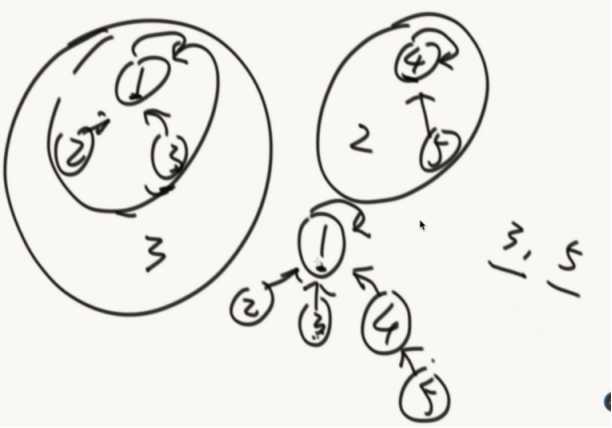
自己指向自己的就是代表节点。

 

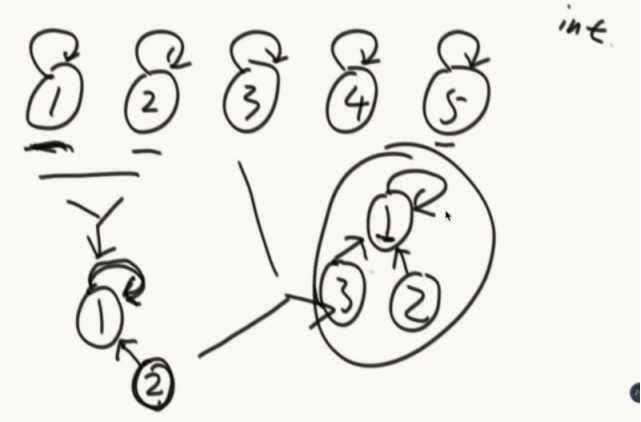
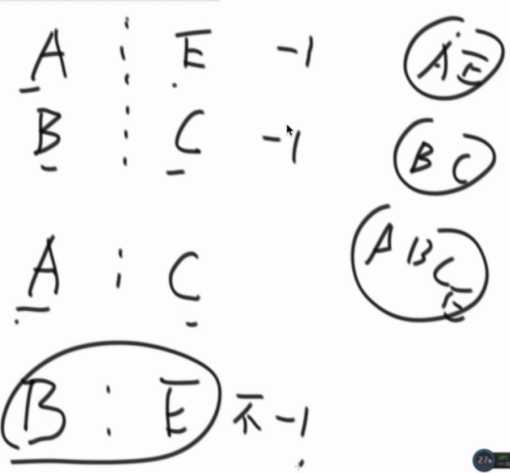
A/B向上找代表节点，相同就是在同一个集合。

 

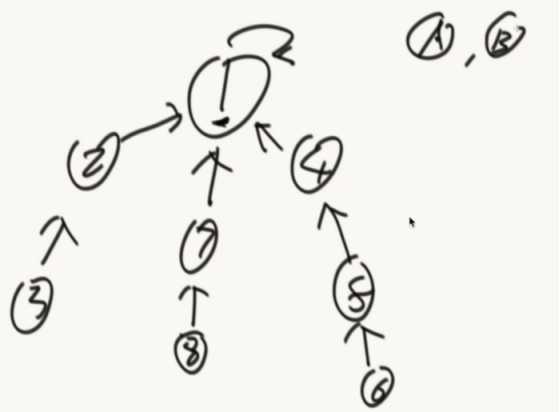
怎么合并

少元素的挂在多元素的底下。

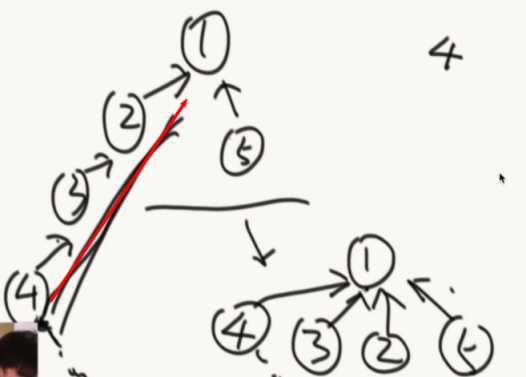
优化：（路径压缩）

在一次查询后，把路径上的节点统一打平。

 

 

public class Code_04_UnionFind {

    public static class Node {
        // whatever you like
    }

    public static class UnionFindSet {
        public HashMap<Node, Node> fatherMap;
        public HashMap<Node, Integer> sizeMap;

        //创建的时候就要一次性导入所有的节点
        public UnionFindSet(List<Node> nodes) {
            fatherMap = new HashMap<Node, Node>();
            sizeMap = new HashMap<Node, Integer>();
            makeSets(nodes);
        }

        private void makeSets(List<Node> nodes) {
            fatherMap.clear();
            sizeMap.clear();
            for (Node node : nodes) {
                fatherMap.put(node, node);//一开始自己是自己的父亲
                sizeMap.put(node, 1);//大小为1
            }
        }


        private Node findHead(Node node) {
            //获得节点的父节点
            Node father = fatherMap.get(node);
            if (father != node) {//这样找是因为头节点是自己指向自己的
                //一路向上找父节点
                father = findHead(father);
            }
            fatherMap.put(node, father);//路径压缩
            return father;
        }
        
        public boolean isSameSet(Node a, Node b) {
            return findHead(a) == findHead(b);
        }

        public void union(Node a, Node b) {
            if (a == null || b == null) {
                return;
            }
            Node aHead = findHead(a);
            Node bHead = findHead(b);
            if (aHead != bHead) {
                int aSetSize= sizeMap.get(aHead);
                int bSetSize = sizeMap.get(bHead);
                if (aSetSize <= bSetSize) {//a小于b
                    fatherMap.put(aHead, bHead);
                    sizeMap.put(bHead, aSetSize + bSetSize);
                } else {//a大于b
                    fatherMap.put(bHead, aHead);
                    sizeMap.put(aHead, aSetSize + bSetSize);
                }
            }
        }

    }

    public static void main(String[] args) {

    }

}

 

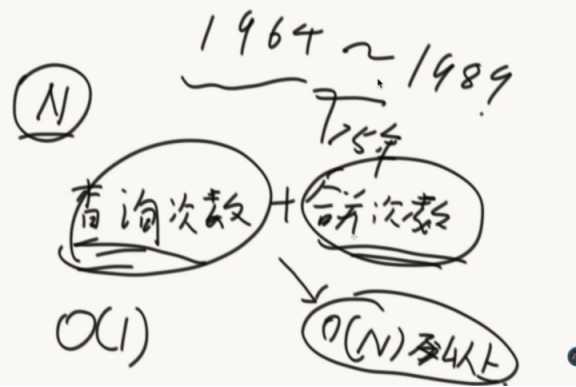
并查集是1964年别人脑补的一个算法，到证明结束是1989年，这个证明也是够漫长的。

并查集的效率非常高，当有N个数据的时候，假设查询次数到了N之后，其时间复杂度仅为o(1)！！

查询次数+合并次数逼近o(n)以上，平均时间复杂度o(1)