如何向嫩模口授blockchain的底层逻辑？

Posted 2021-04-29 金融黑杰克

从2017年大火至今，区块链即使对「圈外」的人士来说也已不是一个陌生概念。我们知道区块链是一个不可篡改的「分布式账本」，我们知道因为「不可更改」，区块链有很大应用潜力。但很多人对区块链的底层工作机制仍不够理解。相关介绍文章有很多，但很多过于偏重复杂技术层面讲解。本文希望通过五个步骤的简单解释，帮助对区块链不熟悉的朋友对其工作机制有一个大致了解。同时为了便于解释，文中个别示例细节没有严格遵照实际技术要求，重在阐述运行逻辑。

 

Step1. 区块是什么？

区块链是一种数据储存的方式。数据以「区块」的方式储存（我们可以想象一堆数据被分别放进相同容量大小的文档里），这些「区块」被连接在一起，目的是使这些数据不可更改。

 

为了更好理解区块链的机制，我们就用最基本的区块链——比特币区块链来解释它的工作机制。对于比特币，它的区块链储存了比特币的交易数据记录。这些数据被分别储存在容量1MB大小的「区块」里。

 

Step2. 如何连接区块？

想象下图的一组区块里储存了一些比特币交易数据。我们可以把这些区块想象成一组容量大小为1MB的文档。

按照交易的时间顺序，区块1记录了第1笔到第N笔交易的数据，发生第N笔交易时，所有交易数据的容量大小刚好为1MB；第二个区块从记录第N+1笔交易开始，容量大小为1MB；以此类推，每个区块的大小均为1MB。

 

那么怎样把这些区块连接在一起？我们可以先给每个区块设置一个独特的（数字）签名，这个签名可以代表这个区块内包含的所有数据内容。如果区块内的任何数据内容（哪怕是一个字符）发生变化，这个区块就会得到一个新的签名。也就是说不同的区块对应一个唯一特定的数字签名。这个过程通过哈希计算得以实现，会在下一个步骤做详细解释。

 

我们假设区块1记录了两笔交易：交易1（小强转给小雅100比特币）与交易2（小明转给小红200比特币）。假设交易1与交易2的数据容量之和为1MB（在实际交易中，交易数量会远远超过2笔）。基于区块1内的交易数据，区块1被赋予了一个特定的数字签名，比如这个签名是「X35」（实际的签名远比这个签名复杂）。记住，区块1内只要有一个数据发生变化，那么区块1就会得到一个不同的签名。

 

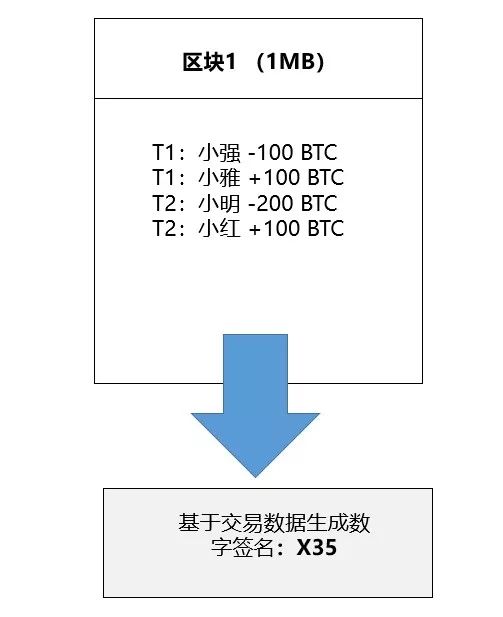
为什么要为区块1设定签名？因为我们可以把区块1的这个签名（也就是X35）添加到区块2的数据里，这样由区块2内的所有数据（包括区块1的签名）生成的签名也可以说有一部分是基于区块1生成的。如下图所示：

 

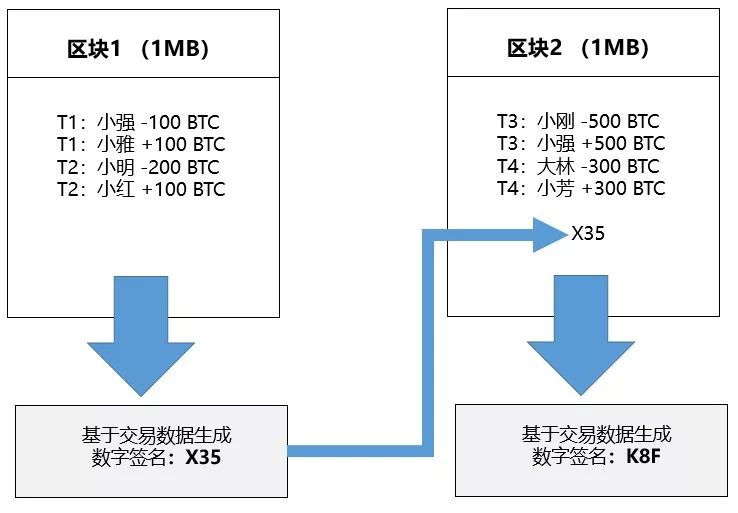
通过添加前一个区块签名的方式，两个相邻区块就被连接在一起，从而使所有区块形成一个链条，也就是「区块链」。如下图所示：

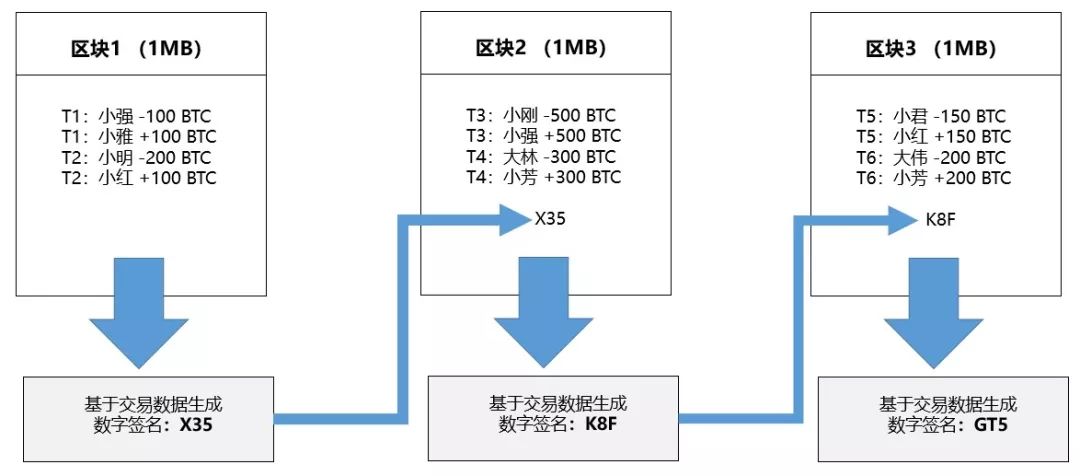
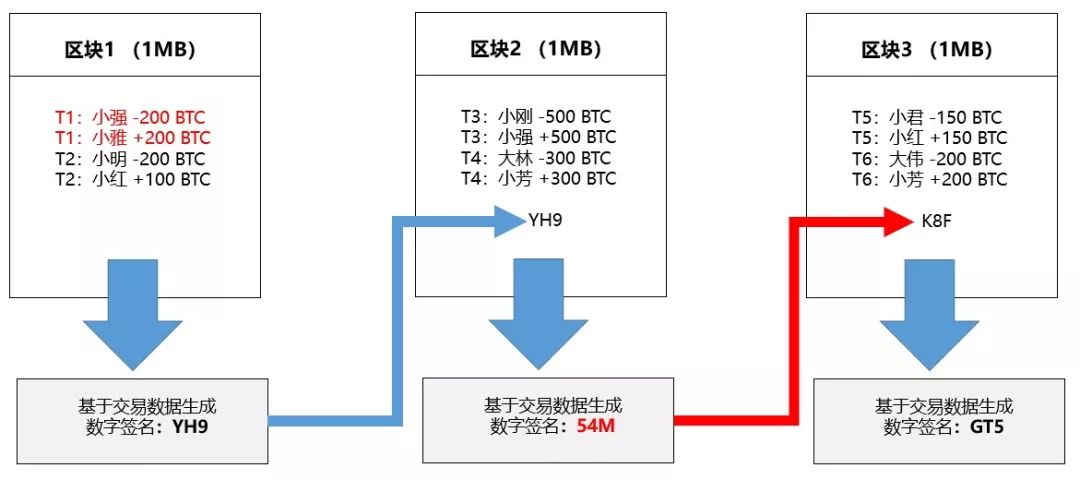
现在想象下，如果区块1内的数据被改动，比如小强发给小雅的比特币数量被改成200个而不是100个，那么区块1的数字签名随之也会发生变化，因为我们知道这个新签名一定要和区块1的新数据相对应。在这里，我们可以假设区块1的数字签名由X35变成了YH9。

 

但问题来了，区块1新生成的YH9与之前被添加到区块2的签名X35并不匹配，这样导致区块1与区块2无法连接在一起，而这会告知区块链上的其他节点区块1中的某些数据已经被改动了。这时他们会通过恢复区块1原有数据的方式拒绝这次修改，这样区块1与区块2仍然会保持连接。

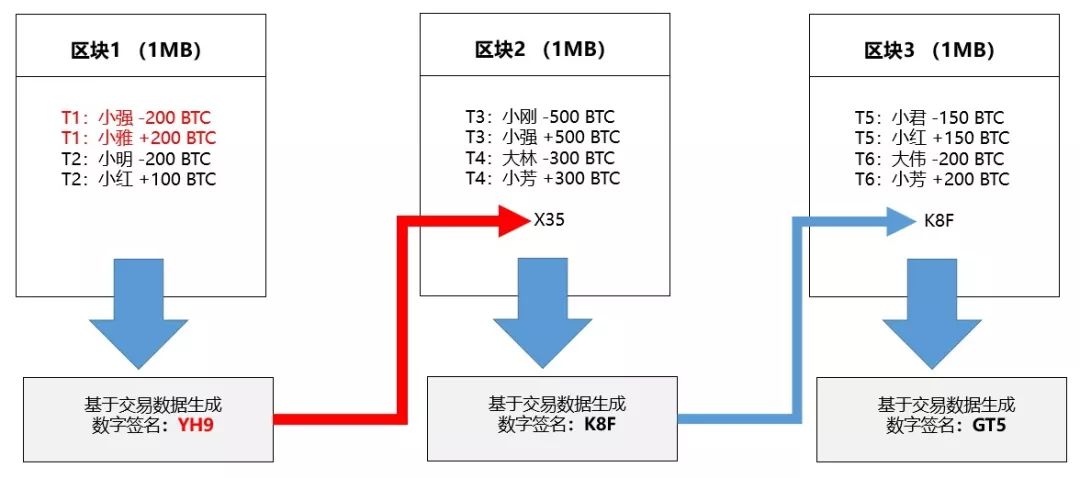
在这种情况下，如果你希望在不被发现的情况下改动区块1内的数据，你不得不用区块1的新签名（YH9）替换掉区块2中的原有签名（X35）。但是如果区块链中的任一数据发生变化，区块2对应的数据签名也会发生变化，比如由原来的「K8F」变更为「54M」，而这会同样导致区块2与区块3无法连接，你不得不将区块三中的旧签名K8F替换为54M。也就是说，改动一个区块内的数据意味着你需要获得后面每一个区块（直至链的末端）的新签名，但这在实际操作中被认为几乎是不可能的。为了理解为什么不可能，我们首先需要了解下区块的签名究竟是如何被创造出来的。

Step3. 如何创造签名？

为了方便理解，让我们再来重新生成一个区块，命名为区块1。区块1里只有一笔交易：小强给小红转了100比特币。区块1的这笔交易信息需要一个数字签名。在区块链中，这个数字签名是通过一种被称为「哈希算法」的加密方式生成。哈希算法是一种非常复杂的数学算法，可以将任意长度的字符串通过运算转换成固定长度的字符串。

 

不同的哈希算法，会对应特定长度的字符串输出。我们以SHA256这种哈希算法为例，它会输出固定64位长度的字符串。比如我们可以输入「发财」这两个字，通过SHA256算法，得到的输出是：

39a8fe2be270ae55e810de4e52d949ec936f0153bd568f0f1d8ccec192c737c7

 

如果输入发生任何改变，得到的输出会完全不同。比如「恭喜发财」这四个字的输出是：

5570fa70c31f391b8a26164508f154bd3878c88d808409c2dbfce9e1c8db79f3

 

而如果在输入前加一个空格，改为「 恭喜发财」，得到的输出则变成了：

b83a7cfdb0a4356fd64a4a5492875f8eb8a202749bd7e3f8bb462a8792c00942

 

通过哈希算法，相同的输入总会得到相同的输出，不同的输入会得到不同的输出。对区块链来说，哈希算法的输入是某个区块内的所有数据，输出则是该区块的数字签名。通过哈希运算可以得到数字签名（也就是哈希值），但通过数字签名我们无法通过反推计算获得原始数据。

 

我们再来看下刚才的区块1：小强转给小红100个比特币。假设区块内数据字符串是：区块1 小强-100 小红+100

 

这个数据字符串经过哈希运算，得到的哈希值（也就是签名）是：

d7915ccddce10056eb4fcf31e58e03e7217ba18b203a0e241d4bd9c0bf5fc08a

 

这个签名需要被添加到区块2中，假设区块2内唯一的一笔交易信息是：小红转给小花100个比特币，那么区块2看起来应该是下面这个样子：

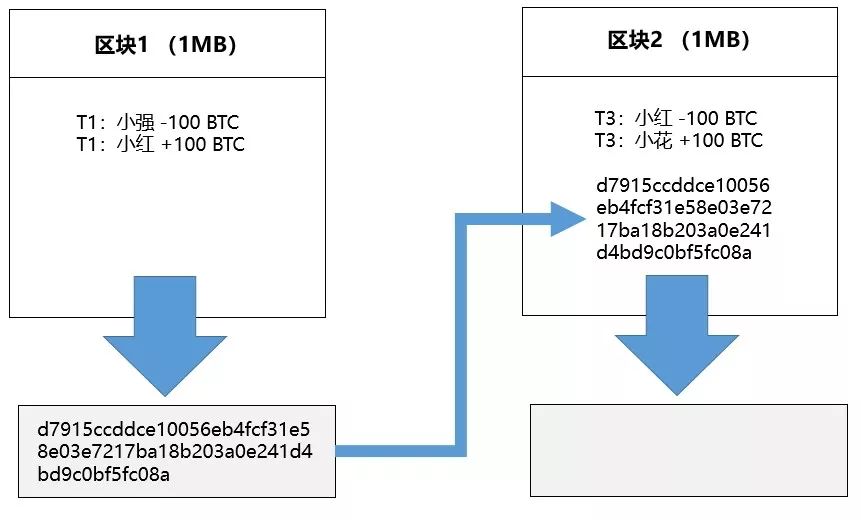
即区块2的数据字符串是：

区块2 小强-100 小红+100

d7915ccddce10056eb4fcf31e58e03e7217ba18b203a0e241d4bd9c0bf5fc08a

 

上述字符串（加粗部分）再经过哈希运算后，我们会得到区块2的签名，即：

9e03c2bd53ca471380d37e0151e2f5d7d19e8da325f4e6af27bb94651be4ff8b

 

通过这种方式，哈希算法可以被用来生成每一个区块的签名。那么，接下来的问题就是，这种签名如何防止「坏人」通过给后面每个区块插入新签名的方式修改某个区块内的数据？解决方案是：输出的数字签名（哈希值）必须满足某种特殊要求。使签名满足这种特殊要求的过程即是我们平时常说的「挖矿」，具体内容我们在下面详细介绍。

 

Step4. 什么样的签名才是合格的签名？

我们刚刚介绍了一个区块的数字签名是如何生成的，但并不是所有的签名都是合格的签名。在区块链里，只有当一个签名以若干个数字0开头时，这个签名才是一个符合标准的签名，其所代表的区块才会被区块链接受。

 

比如，在一个区块里，区块数字签名至少前十位均为0时，这个区块才能被添加到区块链中。但是，正如我们在step3中所提到的，每一个字符串输入都对应一个特定的哈希值输出。如果一个数字签名（哈希值）并不是以10个0开头，我们该怎么办？因此，为了使一个区块的数字签名满足这个要求，这个区块的字符串需要不停变化，直到我们找到一个特定的字符串能使其输出的签名满足这个要求（以10个0开头）。

 

由于区块内的交易数据和元数据（区块编号、时间戳等）必须维持不变，我们只有再给这个区块添加一小段数据。这段数据没有任何意义，只是为了不停地变化，以使区块最终生成一个合格的数字签名（哈希值），这一小段数据被称为区块的「nonce」。Nonce是一段完全随机的数据，形式上可以包括数字、大小写字母、符号等。

所以，一个区块实际由三部分组成：1）交易数据，2）前一个区块的数字签名），3）nonce。持续变更nonce以找到一个合格的数字签名的过程被称为「挖矿」。当然，找到某个特定的nonce以满足签名要求并不容易，需要耗费巨大的算力与电力。耗费的算力与电力越多，挖矿的人或者说「矿工」越有可能更快地找到合格签名。

 

Step5. 如何让区块链「不可更改」？

我们知道，如果要更改某个区块内的数据，我们不得不将后一个区块内包含的「老签名」替换成「新签名」，以使两个区块继续保持连接。也就是说改动区块需要获取后面每一个区块的新签名。刚才我们说了，区块的签名生成有特定的要求，获得所有区块的签名是一个既费时又费钱的过程（消耗大量算力与电力），这件事看起来很难，但好像又不是不可能。但在实际操作中，这种做法的确具有不可操作性，具体原因如下：

 

我们假设有一个「矿工」是坏人，他篡改了一个区块的交易数据，然后努力获得后续所有新区块的签名（也就是「挖矿」），他需要让所有区块保持连接，以让整个网络最终接受他的数据改动。理论上，如果他做到了，那么这次作弊行为也就成功了。但问题是，当他在挖矿时，网络上的其他人也在挖矿。除非这名坏矿工的算力超过网络其他所有矿工的算力之和（也就是拥有整个网络51%的算力），他永远无法追赶上其他所有算力的挖矿速度。

 

区块链是一个分布式网络，理论上世界上任何人、任何组织都可以参与「挖矿」，因此我们可以认为一名「坏矿工」的算力不会超过网络其他算力之和，这也就意味着网络将永远不会接受区块内的任何数据改动，从而使区块链具有「不可更改」的特性，这也是区块链最核心的价值。

 

区块链的这个机制确保了它的安全性，但这里仍会让人产生一个顾虑：万一「坏矿工」获得51%的算力，我们该怎么办？对于这个问题，理论上的确有这种可能。谁获得51%的算力，谁就有能力对区块中的数据进行篡改，这被称为「51%攻击」（我会在以后文章做一个更具体的解释）。但在实际情况中，发动51%攻击耗费的巨大成本（硬件、电力、设备存放、设备冷却等）要远超过通过作弊获得的收益。发动51%攻击即意味着要凭一已之力同网络所有其他用户对抗。因此，参与「挖矿」的用户越多，区块链就会越安全。

 

现在让我们再来稍微梳理一下为什么区块链「不可更改」：因为区块相连的设定，想改动一个区块的数据，必须获得后续每一个区块的数据签名。获得数据签名的过程就是不断变更nonce值得过程。找到特定的nonce要耗费巨大的算力与电力，这个过程被称为「挖矿」。如果一名「坏矿工」想成功改动区块数据，他必须拥有超过网络其他所有用户的算力（也就是51%的算力），以追赶上其他用户的挖矿，最终让网络接受改动的数据。但这件事不具可操作性，因为51%算力耗费的成本要远高于作弊获得的收益，因此区块的数据不会被改动，使区块链具有「不可更改性」。

 

如果我们再提炼下：在区块链里，想作弊，不但要挖矿（挖矿很难同时费钱），而且还必须拥有超过51%的挖矿算力（耗费成本远大于收益），这不被认为具有可操作性。也就是说「挖矿」的机制极大提升了作弊成本。

 

在这里，「中本聪」假定「逐利」是现代人的最大特性（或者说弱点），并利用这个「弱点」来对抗作弊行为。我们现在不能确定利用人逐利的弱点对抗作弊就一定是「最好」的安全机制，但它无疑是一个十分精妙的系统设计。

***

about future & investment