Lingo实战——最短路径问题

Posted 2021-04-28 LINGO与大数据

      今天小布丁为大家分享图论经典问题之一——最短路问题。

      分享案例的网络图及距离如下图所示，其中不可达的路线即使用99999代表无穷大。

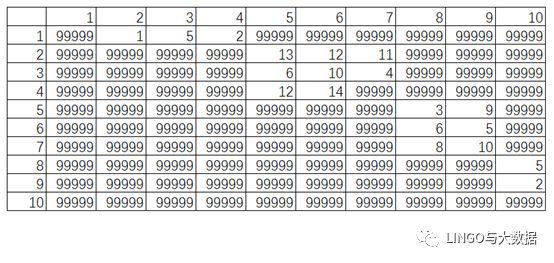
1.Floyd算法

       算法的基本思想是在上一状态集合中插入新的点，来得到新的两点间的最短距离。第k次插入，inter(k,i,j) = min{ inter(k-1,i,j), min{inter(k-1,i,m)+inter(k-1,m,j)}}，ok，了解了算法的核心思想，我们来看看Lingo实现：

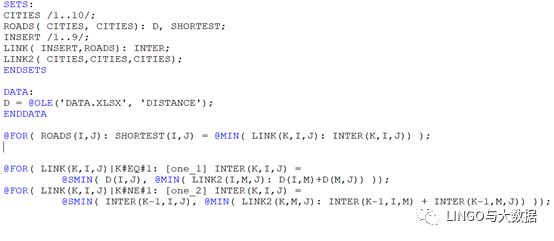
算法注意：

       1.约束表达式1和2作用在于区别第一次插入和非第一次插入。

       2.smin和min的区别，离散点和集合求最小（smax，max亦同）。

       3.该算法可求得任意两点间的最短路径。

2.动态规划法

      动态规划的核心思想就是当前状态最优是由上一个状态递推得到，语言描述有点晕乎，还是看公式：F(i)=min{D(i,j)+F(j)}，F(i)即i到达终点的最短距离。有了这个So Easy的公式，辣么Lingo实现就简单了：

3.Dijkstra算法

       算法核心思路是将顶点分为两个集合（s，u），找出s到u的所有通路，并将该通路的顶点划分到s集合，重复上诉步骤，直到所有顶点全部划到s集合，路径查找完毕。以单源为例，详细实现步骤如下表所示：

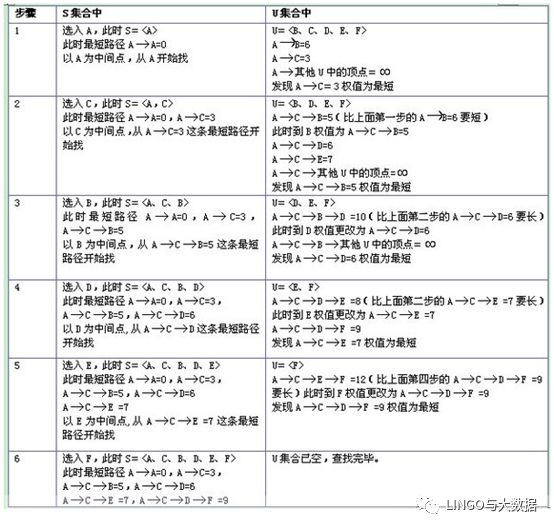
      不知有木有小伙伴发现，单源Dijkstra算法的实现过程本质上就是动态规划的实现过程。有了这个发现，我们将其转化为Lingo实现：

        单源Dijkstra算法可求得从出发点至其余所有点的最短路径。

4.整数线性规划法

       这里介绍Lingo软件提供的一个精炼模型，值得大家仔细研究。其建模的思路非常值得大家学习和研究，利用线性规划模型便求得网路图的最小树，即整个网络图任意两点间的最短路径。但这个模型也有缺点，那就是当网络图顶点过多时，该算法计算效率将大幅降低。

        通过上面四种算法的实现，细心的小伙伴可能已经在思索，模型在实现过程中，有时候需要在Lingo编译过程中做一些调整，达到实现模型但又可以使用Lingo编译的平衡点。而要做到这样灵活自如的编译，没有别的路径，唯有多练习和实践，并且吃透模型的本质。

注：有好的学习经验愿意分享给小伙伴的请随时联系我，有疑问或者建议也请不要沉默。