怎么计算二进制数的运算

Posted 2023-03-17

二进制数相乘可以直接按照十进制乘法进行，或者转化为十进制数后相乘，再将结果转化为二进制数。

下面结合具体两个实例加以说明：

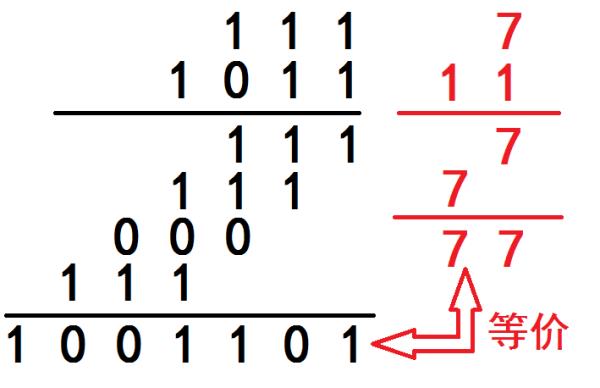
（1）二进制数111乘以1011，乘数1011的每一位分别与乘数相乘，得到111、1110、00000、111000，将其加起来，得到1001101，这便是二进制乘法最直接的解求过程；也可以将111转化为十进制数7，1011转化为十进制数11，显然7乘以11等于77，再将十进制数77化为二进制数1001101，显然1x2^6+1x2^3+1x2^2+1x2^0=64+8+4+1=77，所求结果完全正确。

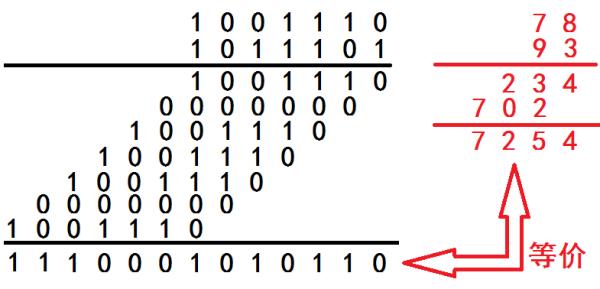
（2）在汇编语言的乘法指令中，其本质就是按照二进制的最直接的乘法运算法则进行的，同上述前一个过程中的算法过程一样。4EH和5DH在计算机中都以二进制代码存储，分别为1001110和1011101，求解的算法过程草稿如上图所示，得到的结果为1110001010110，将结果转化为十六进制数，即是1C56H。当然，这里也可以在乘法执行前，将乘数和被乘数转化为十进制，得到结果7254后再转化为二进制，最后再转为十六进制，过程会相对繁琐一些。

参考技术A

最简单的计算，就是加一了。

你一个一个的往上加就是了。

这一堆苹果，有多少个？

先用十进制，数一下： 1、2、3、4、5、6、7。

你再用二进制数一遍： 1、10、11、100、101、110、111。

递增计数，你会了吗？

逢二进一，你看出来没有？

你倒着数，就是递减计数，减一减一。。。

不懂可追问。

位运算

计算机的整数变量是以二进制的形式存储的，两个数的位运算就是直接将两个数的二进制形式中每一位一一对应，根据一定规则进行每一位的运算。事实上，C++中使用的四则运算，本质上还是位运算，只是对其进行封装之后的结果。也正因此，位运算相对于其他运算而言效率很高。本文简要介绍一些通过位运算进行枚举的技巧。

首先，介绍一些常见的位运算：

1.按位与&：将两个数按位与就是将这两个数的二进制每位进行&，0&0=0&1=1&0=0，1&1=1。

2.按位或|：将两个数按位或就是将这两个数的二进制每位进行|，1|1=0|1=1|0=1，0|0=0。

3.按位异或^：将两个数按位异或就是将这两个数的二进制每位进行^，1^1=0^0=0，0^1=1^0=1，其本质是不进位加法。

4.按位取反~：将一个数按位取反就是将这个数的二进制每位进行取反，~1=0，~0=1。

5.左移<<：将一个数左移k位就是将这个数乘2^k 。

6.右移>>：将一个数右移k位就是将这个数除以2^k 。

运用位运算进行枚举，一般思路是将数字看成一个01串，每一位是0还是1代表了一个状态。由此，可以用一个整数表示一个最多有64个元素的集合。同时可以综合运用各种位运算实现状态之间的快速转换，从而达到快速枚举的目的。因为枚举很多时候是想不出正解之后的暴力行为，因此题目大多不会为精巧的位运算枚举设置部分分。然而在一些状压DP中，对状态预处理时的枚举进行优化却往往能获得意想不到的效果。

---

 

下面介绍一些常用的枚举方法。

1.枚举子集：

枚举子集大概是位运算枚举里最简单的一种了吧，因为一个n元集合的子集一共有2ⁿ 个子集，如果用一个连续n个1的二进制数来表示的话，从0至这个二进制数中每个数的二进制形式都能恰好表示成一个该集合的子集，因此枚举时初状态为0，子集之间状态的转移就是二进制数每次++，末状态为连续n个1的二进制数，也就是2ⁿ -1。

最简单的枚举代码就不贴了吧……

2.枚举n元集合（全集）的k元子集：

一个比较暴力的方法是仍然枚举子集，对每个枚举出来的子集进行判定是否为k元子集，然而这样做为O(n*2ⁿ)，复杂度较大。我们可以通过一些更加复杂的转移使复杂度逼近理论下界，即O(C(n,k))。

以一个状态1011100（设其为x）为例：

首先，求出这个二进制数的lowbit，（关于lowbit请自行百度树状数组相关知识，在此不再赘述），并将x加上lowbit变为1100000（设其为y），实现了状态的初步转换。

接下来我们只需要在末端补上两个1，转换成通用做法即为在末端补上尾部“连续的1的个数减1”个1。然而我们并不计算尾部连续的1的个数，而是继续采用位运算实现。我们惊讶地发现将y取反后和x按位与之后，原尾部这段连续的1就被我们取出来了，然后只需将其除以（lowbit<<1）就能变成末端“连续的1的个数减1”个1，再把它与y按位或就可以了。这样我们就实现了状态之间的转换。再确定初状态为2^k -1，末状态为<2ⁿ ，就可以实现枚举了。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,k;
int rec[100];
int main()
{
    int i,j,base,x,y;
    cin>>n>>k;//枚举n个元素的集合的k元子集 
    base=(1<<k)-1;//最小的作为初状态 
    while(base<(1<<n))
    {
        for(i=0;i<32;i++){if(base&(1<<i)){rec[i]=1;}else{rec[i]=0;}}
        for(i=31;i>=0;i--){cout<<rec[i];}cout<<endl;
        x=base&(-base);//x=lowbit(base) 
        y=base+x;
        base=(((base&(~y))/x)>>1)|y;
    }
    return 0;
}

View Code

 

3.枚举给定集合的子集：

大致意思是给定一个部分元素可能恒为空的集合（比如10100111），求该集合的所有子集。

一个比较暴力的做法是枚举所有子集，与给定集合按位或，通过结果是否为给定集合来判断是否为子集。复杂度仍然较大。

一个改进的方法是基于一个很朴素的思想：给定集合的子集一定比给定集合小。因此我们可以将给定集合作为初状态，每次通过减一来达到状态转移的目的。然而转移之后的状态中可能原本不会有1的现在变成了1（比如求11000的子集，一步转移之后变成了不合法的10111），因此我们只需要将得到的状态和初状态按位与，把不该有的1变成0，得到的一定是合法子集。容易证明（其实是我不会证明），通过这样转移，可以遍历初状态中所有的子集。

代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 string inp;
 4 int tot=0;
 5 int rec[100];
 6 int main()
 7 {
 8     int i,j,base=0,tmp;
 9     ios::sync_with_stdio(false);
10     cin>>inp;int len=inp.length();//读入一个01串 表示集合 
11     for(i=0;i<len;i++)//字符转数字 
12     {
13         tmp=inp[len-1-i]-‘0‘;
14         if(tmp){base+=(1<<i);}
15     }
16     tmp=base;
17     do
18     {
19         for(i=0;i<32;i++){if(tmp&(1<<i)){rec[i]=1;}else{rec[i]=0;}}
20         for(i=31;i>=0;i--){cout<<rec[i];}cout<<endl;
21         tmp=(tmp-1)&base;
22     }while(tmp!=base);
23     return 0;
24 }

View Code