最短路径-3

Posted 2021-04-28 初中数学题解视频

最短路径-3

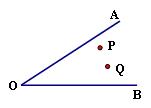
问题二：点P在∠AOB的内部，在OB上找点D，在OA上找点C，使得PD+CD最小。

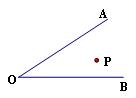
下面我演示一下作图步骤

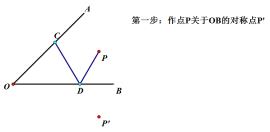
总结：以后看到角的内部一个定点，角的两边上有两个动点这种类型题，第一步：做对称点；第二步：过对称点向其中一条直线作垂线，垂线段的长度即为最小值。

动态演示

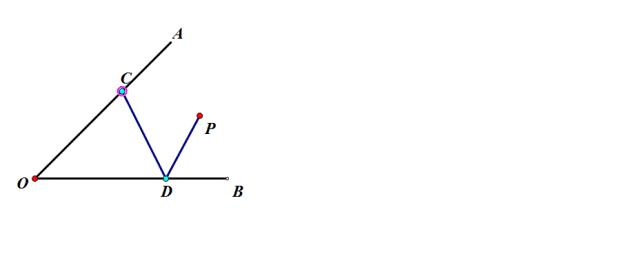
思考一：点P在∠AOB的内部，在OB上找点D，在OA上找点C，使得PC+CD最小，这个提问和问题二一样吗？解决办法一样吗？

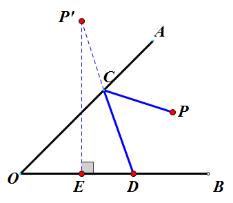
求PC+CD最小值，其实需要作P关于OA的对称点P’，此时PC+CD最小值为P’E的长度。

思考二：点P如果在∠AOB的边上，在OB上找点D，在OA上找点C，使得PD+CD最小，作图方法发生变化了吗？

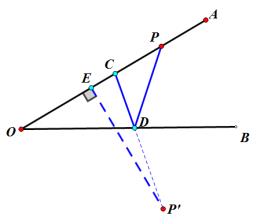
作图方法仍然是过点P作关于OB的对称点P’，再过点P’作垂线，PD+CD最小值为P’E的长度。

思考三：如果点P在∠AOB的外部呢？在OB上找点D，在OA上找点C，使得PD+CD最小，作图方法发生变化了吗？

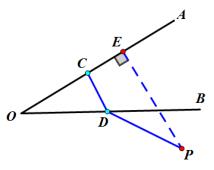
此时PD+CD最小值为PE

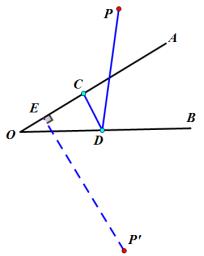
此时PD+CD最小值为P’E

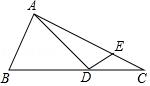
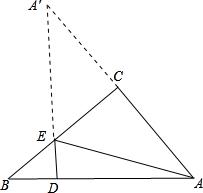
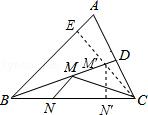
【例】（2018•十堰）如图，Rt△ABC中，∠BAC=90°，AB=3，AC=6倍根号2，点D，E分别是边BC，AC上的动点，则DA+DE的最小值为　　．

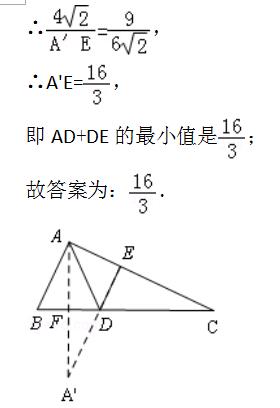
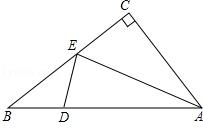
【练习】（2014•鄂尔多斯）如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，D是AB上的动点，E是BC上的动点，则AE+DE的最小值为（　　）

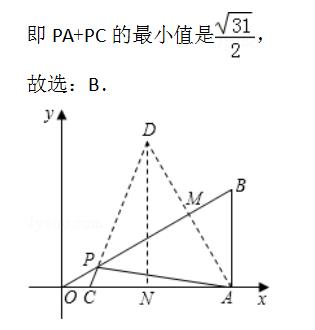
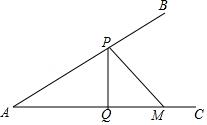
【练习】（2017•泰安）如图，∠BAC=30°，M为AC上一点，AM=2，点P是AB上的一动点，PQ⊥AC，垂足为点Q，则PM+PQ的最小值为　　．

解：作点M关于AB的对称点N，过N作NQ⊥AC于Q交AB于P，

则NQ的长即为PM+PQ的最小值，

连接MN交AB于D，则MD⊥AB，DM=DN，

∵∠NPB=∠APQ，

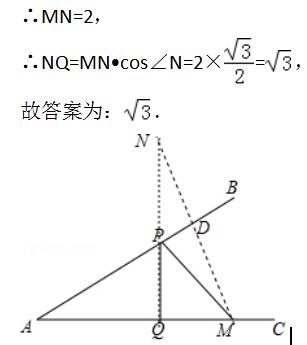
∴∠N=∠BAC=30°，

∵∠BAC=30°，AM=2，

思考四：点P、Q在∠AOB的内部，在OB上找点D，在OA上找点C，使得四边形PQDC周长最小。

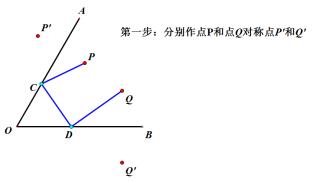
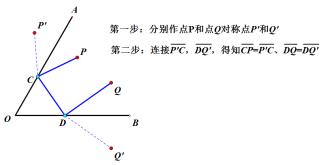
动态演示

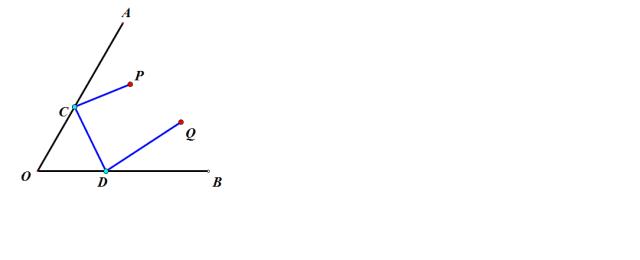
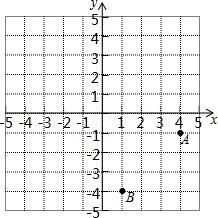
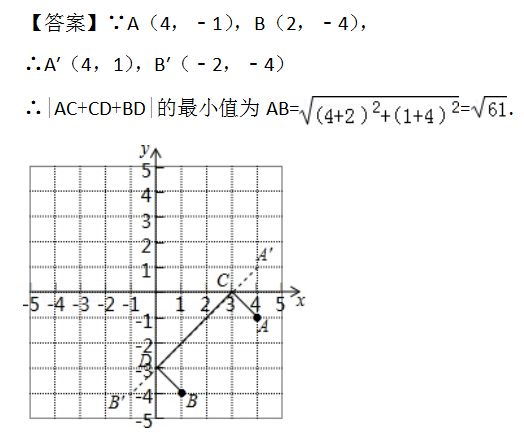
【例】已知，A（4，﹣1），B（2，﹣4），在x轴上找一点C，y轴上找一点D，使|AC+CD+BD|最小，求这个最小值．

【例】（2015•武汉）如图，∠AOB=30°，点M、N分别在边OA、OB上，且OM=1，ON=3，点P、Q分别在边OB、OA上，则MP+PQ+QN的最小值是　　．

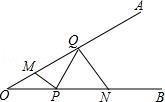
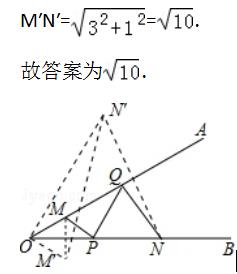
解：作M关于OB的对称点M′，作N关于OA的对称点N′，

连接M′N′，即为MP+PQ+QN的最小值．

根据轴对称的定义可知：∠N′OQ=∠M′OB=30°，∠ONN′=60°，

∴△ONN′为等边三角形，△OMM′为等边三角形，

∴∠N′OM′=90°，

∴在Rt△M′ON′中，

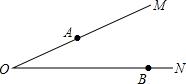
【练习】如图，∠MON=20°，A、B分别为射线OM、ON上两定点，且OA=2，OB=4，点P、Q分别为射线OM、ON两动点，当P、Q运动时，线段AQ+PQ+PB的最小值是（　　）

THE END

最短路径未完，希望大家继续关注