图算法|Dijkstra最短路径算法

Posted 2021-04-28 Python与算法社区

01

—

单源最短路径

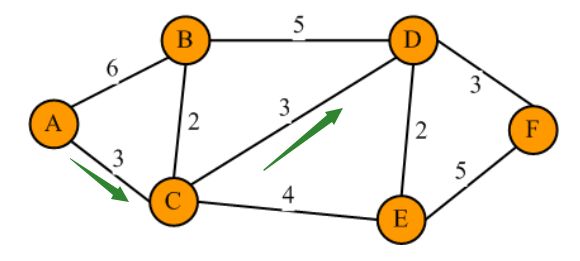
首先解释什么是单源最短路径，所谓单源最短路径就是指定一个出发顶点，计算从该源点出发到其他所有顶点的最短路径。如下图所示，如果源点设为A，那么单源最短路径问题，就是求解从A到B，从A到C，从A到D，从A到E，从A到F的最短路径。

比如，从A到D的最短路径，通过肉眼观察可以得出为如下，A->C->D，距离等于3+3=6，其中A->C边上的数值3称为权重，又知这是无向图，从C到A的权重也为3。

02

—

Dijkstra算法求单源最短路径

这个算法首先设置了两个集合，S集合和V集合。S集合初始只有源顶点即顶点A，V集合初始为除了源顶点以外的其他所有顶点，如下图所示：

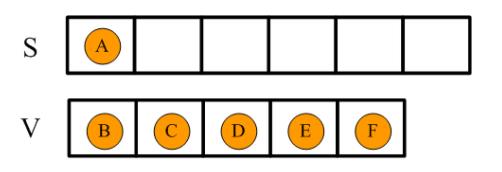
设置一个从A到各顶点的缓存字典，作为算法的输出，初始时，统一设置为 -1，

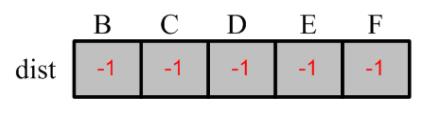
接下来，开始求解A到某个节点的第一个最短距离，通过邻接矩阵，我们自然可以找到与A存在边连接的所有顶点，即顶点B，顶点C；

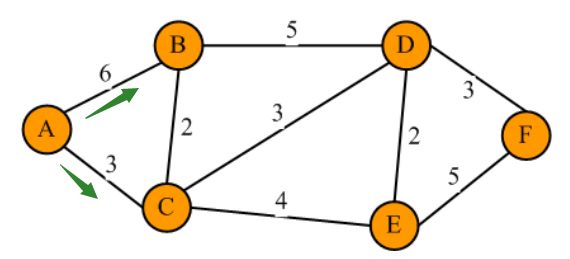
Dijkstra算法会选择A->B，A->C的距离最小的，挑选C，放入S集合中，但是更新dist字典的时候，可以同时更新A->B和A->C的距离，示意图如下：

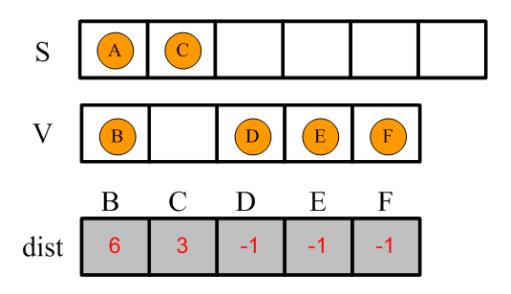
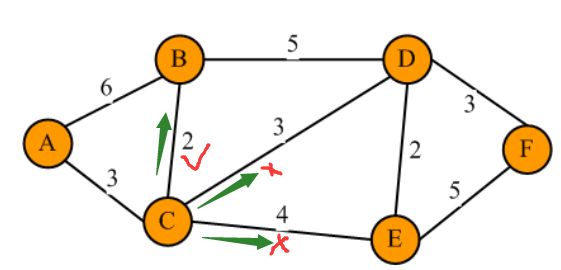
再进一步，找S集合的最后一个元素C在V中与之关联的所有边：B，D，E，因此

A->B = 3 + 2 =5

A->D = 3 + 3 = 6

A->E = 3 + 4 = 7

根据Dijkstra算法，选取最小距离，即B进入S集合，并且，Dijkstra算法要和dist字典中A->B 距离做一次比较，

如果dist(A->B)!=-1，且5 <= dist(A->B)，则更新dist(A->B)=5；

如果dist(A->B)!=-1，且5 > dist(A->B)，则不更新dist(A->B)；

注意，根据这种讨论，实际上我们考虑了两种从A到B的路径：A->B，A->C->B，但是到达B的路径不只这两条，因为经过D也可以到B，如果这些路劲中出现比距离5还小的路径的话，那么Dijkstra算法是不是有漏洞呢？这个考虑是正确的，但是Dijkstra算法假定了边的权重值必须大于0，这样的假定，可以避免经过D到B的路径不可能小于5，因为除了A->B外，其他所有达到B的路径必然经过C，与C相连的顶点中，到达B是最小的，所以经过其他边到达B后，距离不可能小于5。

以上分析就是Dijkstra算法的基本思想，直到集合V的元素个数为0为止，最终的dist字典如下：

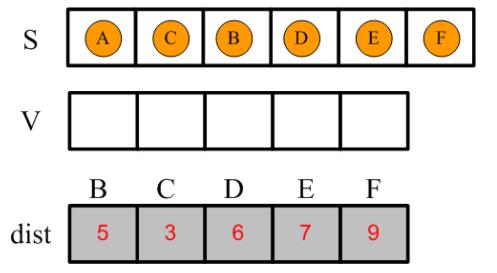
03

—

Dijkstra算法总结

算法的基本思路：

1. 初始化两个集合，S集合和V集合。S集合初始只有源顶点即顶点A，V集合初始为除了源顶点以外的其他所有顶点，dist字典值都为-1；紧接着，根据邻接矩阵，找出与A存在边的顶点list，遍历list，依次更新dist字典（比如list={B,C}，则依次更新字典键为B,C 的距离值）, 求出与 A 距离最近的顶点，并从V集合中移除到S集合中；

2. 抓出S集合的最后一个元素，根据邻接矩阵，找出V集合中与之存在边的顶点list，遍历list，求出与之距离最小的顶点，并从V集合中移除到S集合中。

3 dist更新，分情况讨论，如果遍历到的顶点不是与之最小的顶点，则直接更新dist字典，比如list={D,E}，则依次更新字典键为D,E的距离值，如果遍历到的顶点是与之最小的顶点，则需要判断dist[此顶点]与当前的距离，如果后者小，才更新dist[此顶点]，否则不更新。

4. 重复2和3，直到V集合元素为空为止。

《实例》阐述算法，通俗易懂，助您对算法的理解达到一个新高度。包含但不限于：经典算法，机器学习，深度学习，LeetCode 题解，Kaggle 实战。期待您的到来！