数据挖掘算法：PageRank

Posted 2021-04-27 算法爱好者

（点击上方公众号，可快速关注）

http://www.cnblogs.com/en-heng/p/6124526.html#mjx-eqn-eqpr2

1. 引言

PageRank是Sergey Brin与Larry Page于1998年在WWW7会议上提出来的，用来解决链接分析中网页排名的问题。在衡量一个网页的排名，直觉告诉我们：

1、当一个网页被更多网页所链接时，其排名会越靠前；

2、排名高的网页应具有更大的表决权，即当一个网页被排名高的网页所链接时，其重要性也应对应提高。

对于这两个直觉，PageRank算法所建立的模型非常简单：一个网页的排名等于所有链接到该网页的网页的加权排名之和：

PRi表示第i个网页的PageRank值，用以衡量每一个网页的排名；若排名越高，则其PageRank值越大。

网页之间的链接关系可以表示成一个有向图代表了网页j链接到了网页i；Oj为网页j的出度，也可看作网页j的外链数（ the number of out-links）。

假定P=(PR1,PR2,⋯,PRn)T为n维PageRank值向量，A为有向图G所对应的转移矩阵，

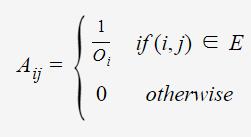
n个等式(1)可改写为矩阵相乘：

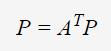
但是，为了获得某个网页的排名，而需要知道其他网页的排名，这不就等同于“是先有鸡还是先有蛋”的问题了么？幸运的是，PageRank采用power iteration方法破解了这个问题怪圈。欲知详情，请看下节分解。

2. 求解

为了对上述及以下求解过程有个直观的了解，我们先来看一个例子，网页链接关系图如下图所示：

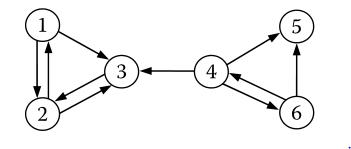
那么，矩阵A即为

所谓power iteration，是指先给定一个P的初始值P0，然后通过多轮迭代求解:

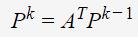
最后收敛于||Pk−Pk−1||<ξ，即差别小于某个阈值。

我们发现式子(2)为一个特征方程（characteristic equation），并且解P是当特征值（eigenvalue）为1时的特征向量（eigenvector）。为了满足(2)是有解的，则矩阵A应满足如下三个性质：

1、stochastic matrix，则行至少存在一个非零值，即必须存在一个外链接（没有外链接的网页被称为dangling pages）；

2、不可约（irreducible），即矩阵A所对应的有向图G必须是强连通的，对于任意两个节点u,v∈V，存在一个从u到v的路径；

3、非周期性（aperiodic），即每个节点存在自回路。

显然，一般情况下矩阵A这三个性质均不满足。为了满足性质stochastic matrix，可以把全为0的行替换为e/n，其中e为单位向量；同时为了满足性质不可约、非周期，需要做平滑处理：

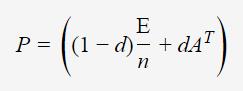
其中，d为 damping factor，常置为0与1之间的一个常数；E为单位阵。那么，式子(1)被改写为

3. 参考资料

[1] Bing Liu and Philip S. Yu, "The Top Ten Algorithms in Data Mining" Chapter 6.

数据挖掘算法系列：

• 
  

觉得本文有帮助？请分享给更多人

关注「算法爱好者」，修炼编程内功