Sketch2Code 微软:手绘UI稿生成前端代码项目
Posted SharingByShira
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Sketch2Code 微软:手绘UI稿生成前端代码项目相关的知识,希望对你有一定的参考价值。
机器智能 - 前端代码生成
问题背景:CustomVision.AI是微软面向大众提供的,用于手绘稿识别的深度学习服务,目前支持C#和Python开发。Sketch2Code是利用该服务来实现,将手绘UI稿转换为前端代码的项目。UI稿识别除了深度学习还有很多方法,比如R-CNN及其优化模型等等图像(物体)识别模型。本文将着重分析其中的部分功能:重构识别结果的数据结构。该变换将便于之后的前端代码生成,所以具有学习价值。
问题描述:转换图像识别结果的数据结构,使数据结构更利于生成前端代码。
输入:前端组件列表。
输出:前端组件层级结构。
目录
项目简介:介绍项目文件目录,分析问题
- 项目信息:项目的代码库
- 文件目录:找到问题核心算法的实现模块
- 问题由来:核心问题的成因、解决思路及意义
数据结构变换:分析数据结构变换的过程
- 问题分析:分析问题并确定算法的数据依据
- 程序设计:针对问题和数据依据设计解决方案
- 代码结构:依据函数调用进一步解析文件目录,定位核心算法的实现文件
- 代码实现:依据解决方案解释算法的实现过程
算法优化:针对异常情况提出解决方案
代码生成:简单介绍前端代码生成的过程
项目简介
项目信息
Sketch2Code(C#):深度学习智能生成前端代码项目,通过识别手绘UI稿中的组件和位置,将其识别结果信息转换为前端代码,主要是View层的html代码,目前服务的测试数据UI稿都是PC端的网页。
https://github.com/Microsoft/ailab
项目GitHub代码库拉取命令:
git clone https://github.com/Microsoft/ailab.git
项目成果展示网站:
https://sketch2code.azurewebsites.net/
文件目录
拉取项目代码库后,我们来看看其文件目录:
(只想了解算法,不想完整学习整个项目代码的朋友可以跳过文件目录分析的各个部分内容。)

分析了项目的文件目录,就能清晰知道其功能模块的划分,从而找到我们想要研究的核心模块的位置,也就是Sketch2Code.Core数据结构转换部分。
问题由来
下面我们通过分析前端页面结构和其实际组成组件的数据结构的关系,来直观的了解一下本文分析的核心模块,也就是数据结构变换存在的意义。
通过一张手绘UI稿,看一下网页页面有哪些元素,和这些元素构成网页的结构:
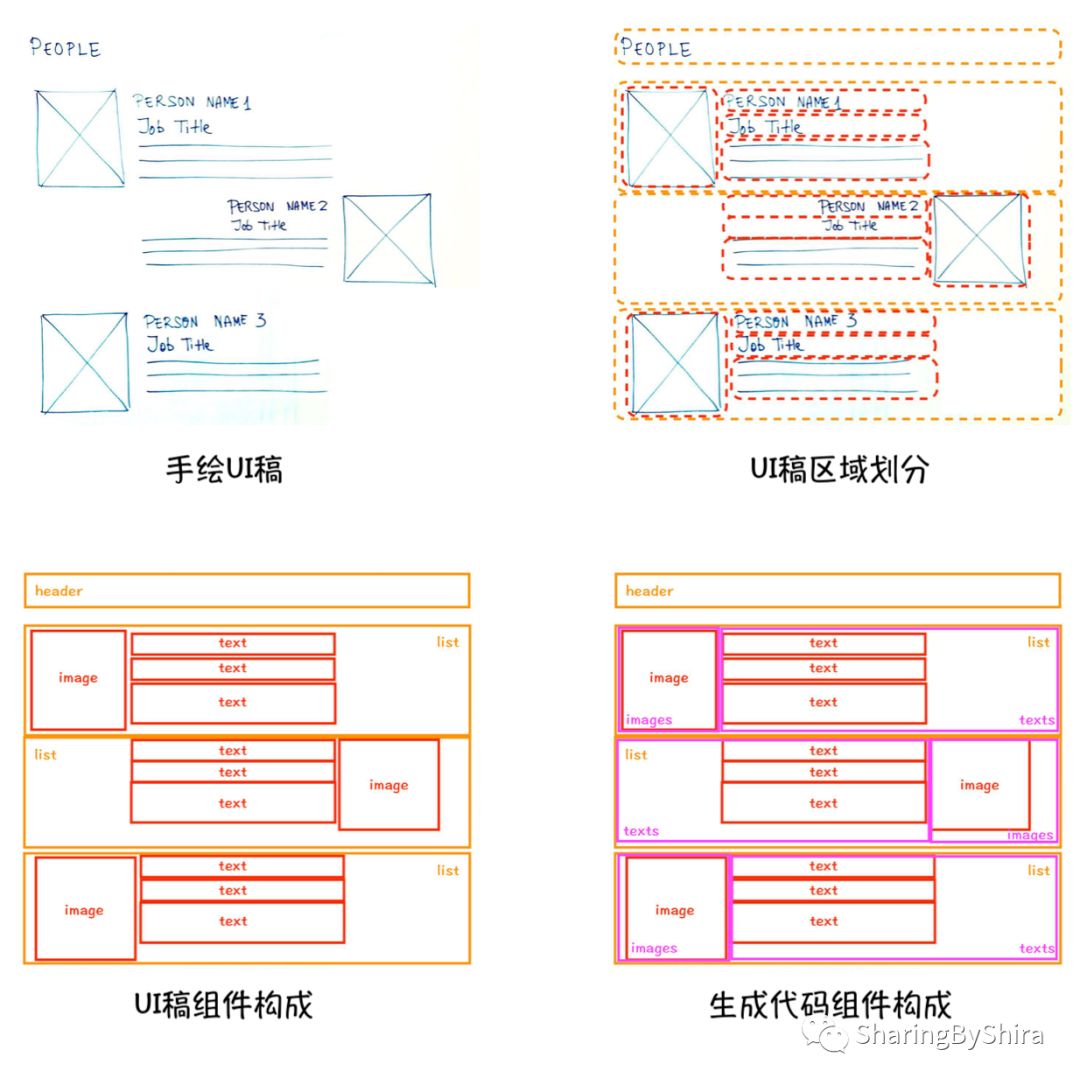
从上图我们可以观察得到,页面组件之间存在层级的包含关系。容器中包含了组件,从而形成了父子层级关系。我们用列表来表现上图中的包含关系,就得到层级的数据结构。
从下图的数据列表中我们可以更直观的感受到观察到的页面数据结构的层级结构。然而深度学习的识别结果却有点不尽如人意,是平铺的列表形式。所以我们才需要做数据结构转换这一步,方便后期层级化的生成前端页面代码。
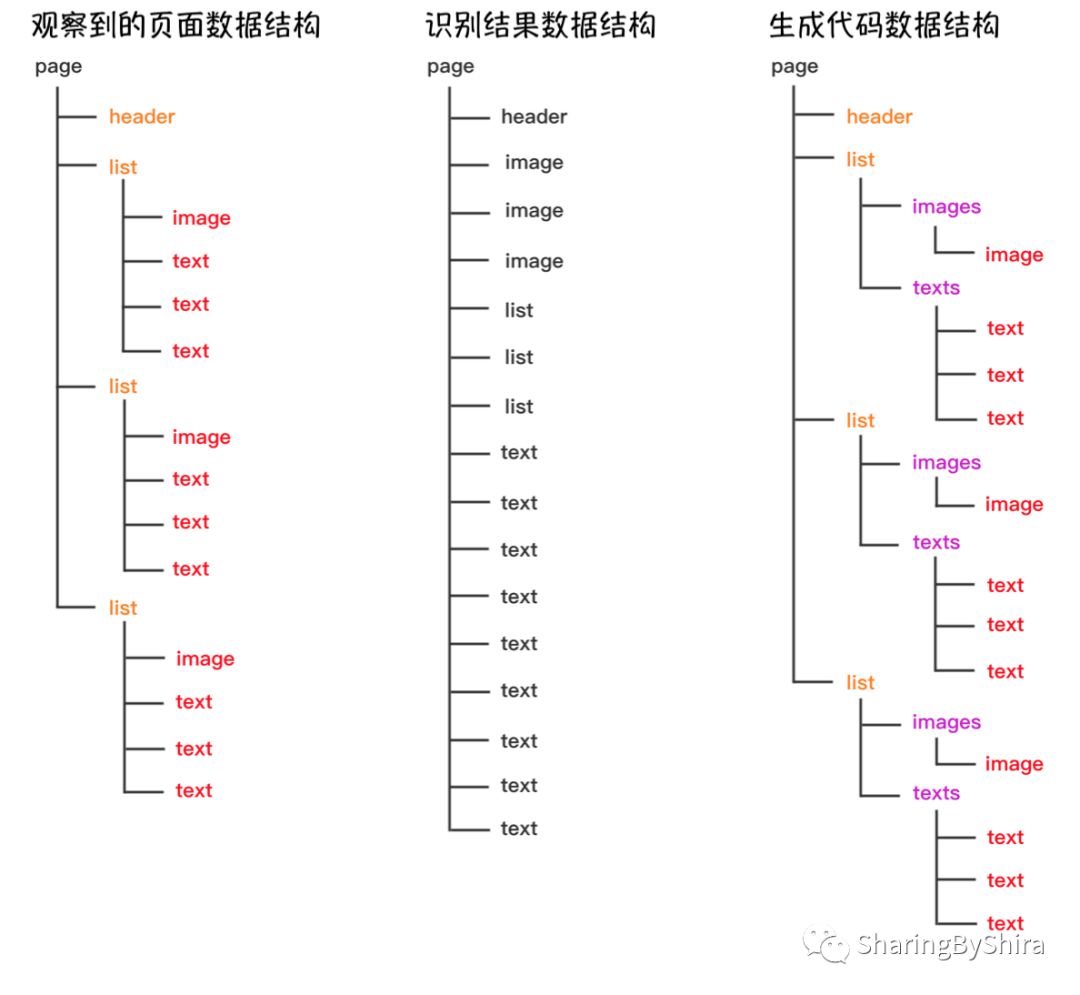
为什么观察到的页面数据结构不能直接用来生成前端代码?
Sketch2Code算法用于生成前端页面代码的数据结构,和我们人眼观测到的页面数据结构(组件结构)有所不同。这是由于前端组件由HTML来实现的,而HTML规定了页面子组件根据其特性只能横向或者纵向排列(这里我们不考虑加入CSS的绝对定位等脱离文档流的定位方式,只用HTML元素原本的特性)。
观察到 list 中的组件的排列方式呈现得过于复杂(横纵兼有),利用HTML规范较难实现(需要辅助CSS定位),也就无法直接用程序生成这样的排版结构。于是我们尝试将其组件进一步层级化(生成代码组件构成图),此时可以看到,在插入的容器 texts 中,其子元素 text 是纵向排列的;images 中,image 也是纵向排列的(只有单一组件的情况下也可以理解为横向排列,但是为了在同级子层保持对齐方式的统一,我们在这个例子中理解为纵向排列)。这样修改后的数据结构,在每一个容器中的组件都只有横向或者纵向单一的排列方式,使得程序能更方便的生成前端代码,且使其构成严格符合HTML规范,从而得到可控的页面排布结果。
由于页面本身就是最大的容器,所以排列规律如下:
页面容器:组件纵向排列;
容器:组件横向排列;
容器:组件纵向排列。
可以看出这是一个(容器 - 组件)递归的过程,从页面容器往下层递归,组件在容器中的排列方式呈现出 纵向 - 横向 - 纵向 ... 交替 的过程。下面的算法就将利用这两个特点来重构识别结果的数据结构。
HTML元素分为:行内元素、块状元素。在特定情况下还存在行内块状元素,其特性会兼有行内和块状元素的特性。(CSS属性可以部分修改这些特性,引入不可控的因素,所以我们在生成代码的过程中尽量不考虑引入此类的CSS属性。)
行内元素(例如 span):横向排列,尾部可以添加其他的HTML元素。

块状元素(例如 div):纵向排列,每个块状元素独占一行。只能在其下方添加其他HTML元素。

当在一个容器中同时加入行内元素和块状元素,那么就会呈现出很多不可控的前端效果。所以为了控制前端页面组件的排布,我们规定在父容器中的子组件只能使用一种排列方式(横向/纵向),更便于程序化的实现生成代码这个过程。
数据结构转换
问题分析
问题:平铺组件列表 --> 层级组件列表
输入:平铺组件列表,包含组件的(名称、位置、长宽)属性信息。
输出:层级组件列表(可以直接生成前端页面代码的数据结构)。
数据依据:分析上个模块图中的UI稿组件构成,我们可以知道前端页面是由不同组件通过确定其位置的组合得到。所以我们将以位置属性为依据来重构组件的数据结构。再结合长宽信息,我们就可以确定一个组件在页面中的占位。
重构方式:在上文的数据结构的分析中,基于HTML元素特性我们得出了两个要点。
1. 递归遍历:从页面容器开始,向内层寻找属于每个父容器的子组件,也就是把子组件归类到父组件的内部。
2. 方向单一:每个父容器内部排布子组件的方向必须是横向或者纵向其中之一。
核心问题:如何利用位置来归类父子组件?
位置(x, y)一般是描述了组件左上角的坐标。x 对应了页面的横向,y 对应了页面的纵向,单独看 x 方向,以页面左上角为坐标原点(0,0),则 x 的增长就意味着组件在横向方向上的排布次序, y 的增长确定了组件在纵向方向上排布次序。
程序设计
数据结构:
1. 把每一个父容器当成一组子组件的集合,我们认为父容器是一个组 Group。
2. 父组件需要指明其内部子组件的排布方式,横向 X 或者纵向 Y。
3. 父组件本身的定位,横纵坐标(x, y)和宽 Width 高 Height。
4. 父组件内部是否还有子组件 is empty?(即是否本组件是层级中最后一层的子组件)
5. 父组件内部的子组件组合 Boxes(由于每一个组件的形状类似一个长方形,所以我们认为组件是一个方形盒子 Box)。
首先父容器和子组件在形态上是一样的,都拥有上面所描述的这些信息。唯一不同的是子组件根据其内容的不同,会对应于不同的HTML元素。而父容器没有特定对应的HTML元素,只要符合内部元素横向排列和纵向排列的规则的HTML元素都可以作为父容器。
算法步骤:
1. 设计一个递归,使得层级数据结构能够根据实际的数据情况动态的增加层数,每一次递归,只生成一层父容器的数据(包含上面数据结构的所有内容)。
2. 设计递归内部父子组件的归类策略:
2.1 根据本层组件的排列方向,在父组件中生成均分的 n 个片段。
2.2 遍历其余组件,将符合条件的子组件加入上面生成的 n 个片段中。
2.3 利用组件间隙(即空白片段)划分区域(合并相邻且不为空的片段),去除片段内重复的子组件,每一个区域成为新的父组件,往其内部寻找其子组件集合(继续递归)。
递归的完成条件:父容器组件内部为空,或内部只有一个子组件,则完成本层递归。
算法过程举例:
1. 页面区域
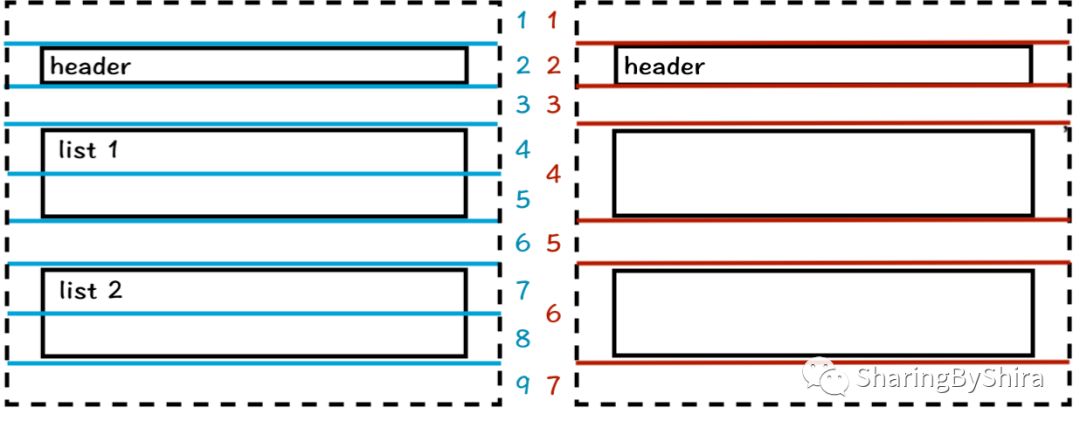
1. 从页面(虚线框)开始往内部递归,把页面看作一个完整区域;
Section: boxes = [header,list 1,list 2]
2. 归类该层的子组件:
2.1 假设本层的排列方式为纵向 Y,将该层均分 n 个片段,设 n = 9;
2.2 遍历子组件将其加入 n = 9 个片段中:
Slice 1: is_empty = true,boxes = []
Slice 2: is_empty = false,boxes = [header]
Slice 3: is_empty = true,boxes = []
Slice 4: is_empty = false,boxes = [list 1]
Slice 5: is_empty = false,boxes = [list 1]
Slice 6: is_empty = true,boxes = []
Slice 7: is_empty = false,boxes = [list 2]
Slice 8: is_empty = false,boxes = [list 2]
Slice 9: is_empty = true,boxes = []
如果父容器 list 1 里面存在子组件 item 1、item 2、... ,那么该片段就会变成这样 Slice 4:is_empty = false,boxes = [list 1,item 1, item 2 ... ],这样保证了父容器和其可能的子组件会被划分到同一个片段和区域中,使得后期可以进一步划分该组件内部的区域。
(这里程序并没有将 list 1 和 list 2 分成两部分,而他们是被重复的加入了不同的片段中,因为其位置被片段包含。这使得后面合并数据时需要去重。)
2.3 利用空白片段(is_empty?) 1、3、6、9,可以将组合并成 7 个区域:
Section 1:boxes = []
Section 2:boxes = [header]
Section 3: boxes = []
Section 4: boxes = [list 1,list 1](去重后)boxes = [list 1]
Section 5: boxes = []
Section 6: boxes = [list 2,list 2](去重后)boxes = [list 2]
Section 7: boxes = []
每个 Section 成为新的父组件,向内递归,此时发现每个父组件的内部 boxes 只有0或1个组件,则递归结束,算法完成。
2. 组件区域
假设 list 1 里面有 子组件 image 和 text 则上文中的:
Slice 4: is_empty = false,boxes = [list 1,image,text]
Slice 5: is_empty = false,boxes = [list 1,image,text]
Section 4: boxes = [list 1,list 1,image,text](去重后)boxes = [list 1,image,text]
此时由于 Section 中的 boxes > 1个,所以我们需要往内部递归:
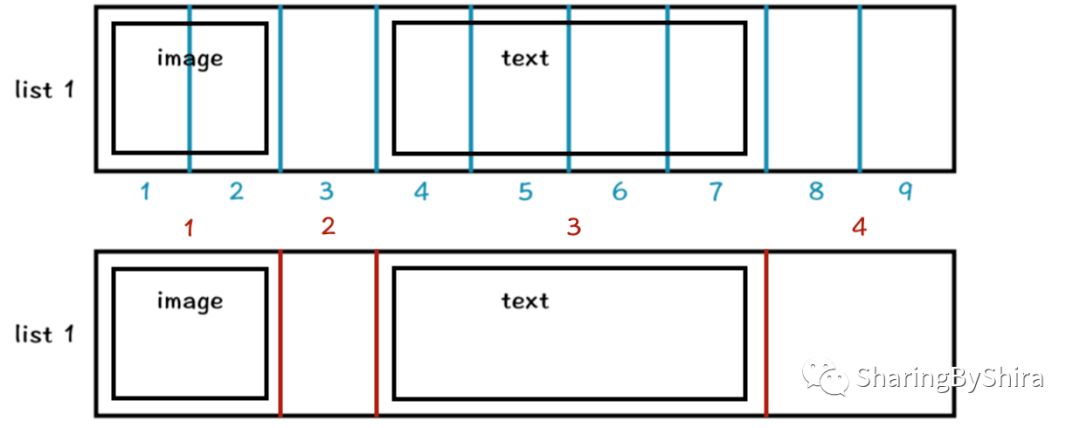
1. 从该层开始往内部递归,该层为一个区域;
Section:boxes = [list 1,image,text]
2. 归类该层的子组件:
2.1 由于上层纵向划分,所以本层的排列方式为横向 X,将该层均分 n 个片段,在同一个算法中 n 的值会保持不变,则 n = 9;
2.2 遍历子组件,将其加入 n = 9 个片段中:
Slice 1: is_empty = false,boxes = [image]
Slice 2: is_empty = false,boxes = [image]
Slice 3: is_empty = true,boxes = []
Slice 4: is_empty = false,boxes = [text]
Slice 5: is_empty = false,boxes = [text]
Slice 6: is_empty = false,boxes = [text]
Slice 7: is_empty = false,boxes = [text]
Slice 8: is_empty = true,boxes = []
Slice 9: is_empty = true,boxes = []
2.3 利用空白片段(is_empty?) 3、8、9,可以将组合并成 3 个区域:
Section 1:boxes = [image,image](去重后)boxes = [image]
Section 2:boxes = []
Section 3: boxes = [text,text,text,text](去重后)boxes = [text]
Section 4: boxes = []
每个 Section 成为新的父组件,向内递归,此时发现每个父组件的内部 boxes 只有0或1个组件,则递归结束,算法完成。
结合页面区域和组件区域的划分过程(先Y后X),我们可以直观的理解相邻的父子组件内部的组件排列是横纵交替的这个规律。每一次遍历完成后的数据结构是这样的:
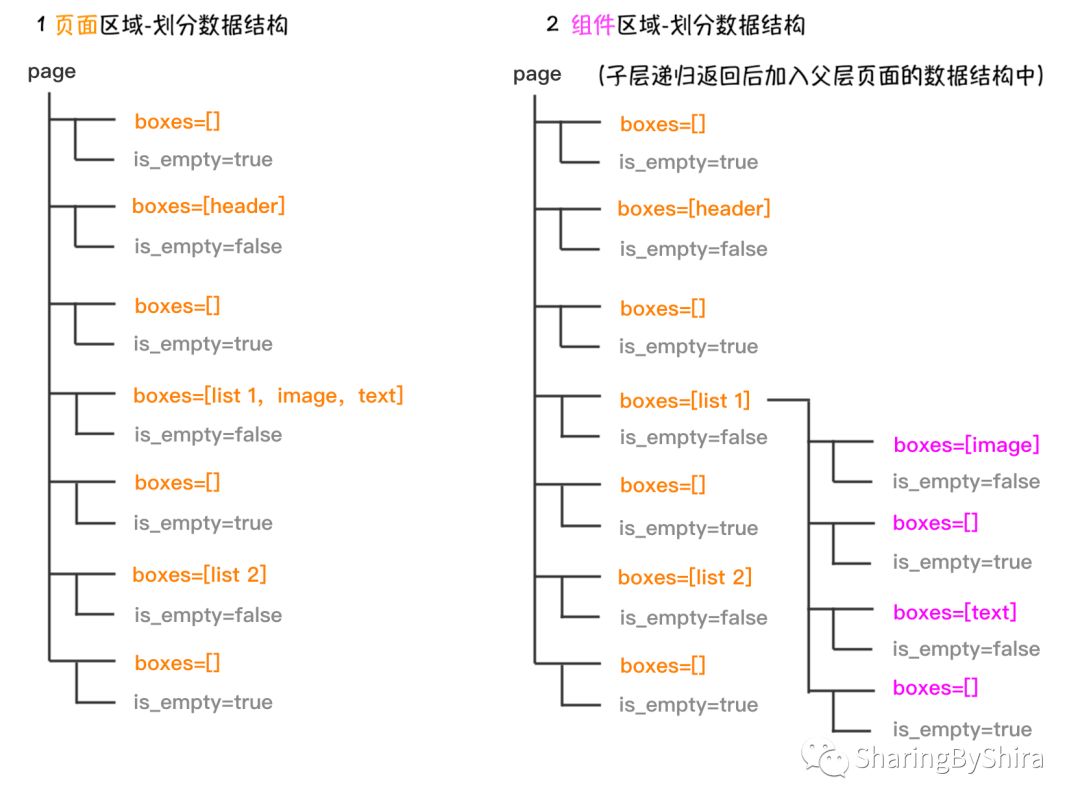
上图中的数据结构和文初的生成代码数据结构有所不不同,是因为我们在算法进行的过程中在数据结构中加入了算法进行所必须的数据,从而使目标结构复杂化了。
代码结构
下图我们将通过分析代码文件的结构找到核心算法的入口,由于在上篇内容的文件目录图我们分析得知,Sketch2Code.Api整合了Core和AI两个模块的功能,恰巧这个模块只有一个代码文件,便于我们分析其逻辑,所以我们从这里开始摸索算法的起始位置。
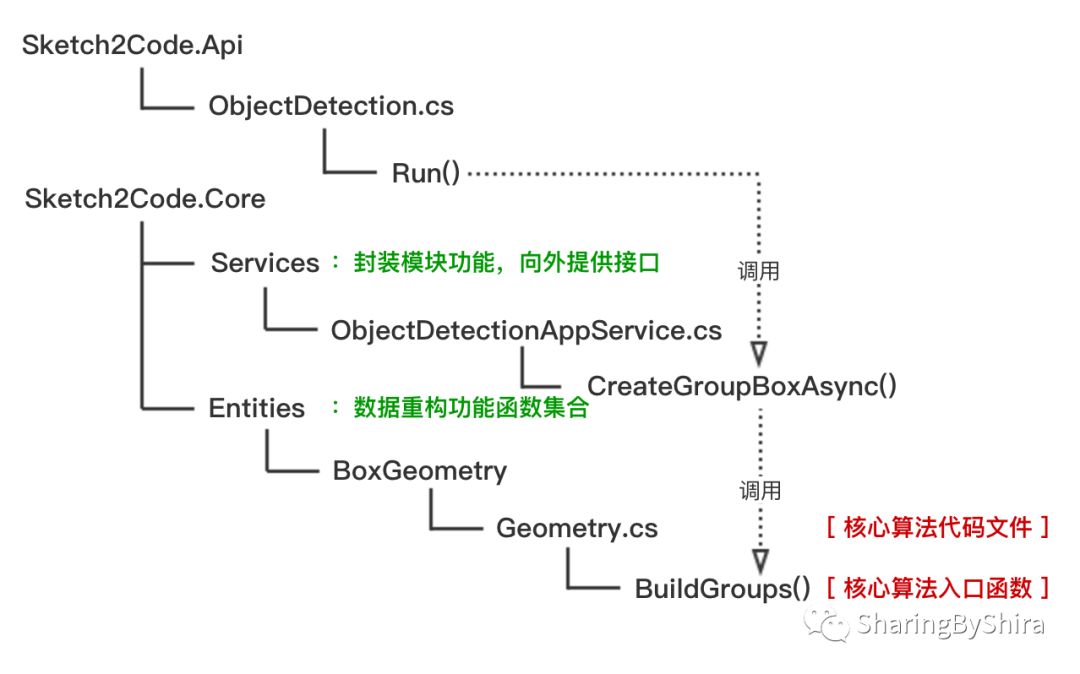
代码实现
我们跟着项目作者的步伐来具体的看一下算法是如何一步步实现的。
1. 设计一个递归,使得层级数据结构能够根据实际的数据情况动态的增加层数,每一次递归,只生成一层父容器的数据(包含上面数据结构的所有内容)。
# 算法的起始函数
# boxes - 识别出的组件列表
public GroupBox BulidGroups(List<BoundingBox> boxes){
GroupBox root = new GroupBox(); # 空节点为顶层父容器,其子组件列表将在递归函数中添加
root.Direction = GroupBox.GroupDirectionEnum.Vertical; # 规定顶层的组件排布方式为纵向(Vertical/Y)
BulidChildGroups(boxes, ProjectionAxisEnum.Y, root); # 开始递归
return root.Groups[0];
}
# 递归函数
# boxes - 识别出的组件列表
# axis - 目前该层父容器内部子组件的排列方向
# parent - 父容器在数据结构里的数据节点
public GroupBox BulidChildGroups(List<BoundingBox> boxes, ProjectionAxisEnum axis, GroupBox parent){
GroupBox g = new GroupBox(); # 空节点为父容器,后续添加其信息和子节点列表
g.IsEmpty = false;
if (axis == ProjectionAxisEnum.X){
g.Direction = GroupBox.GroupDirectionEnum.Horizontal;
} else {
g.Direction = GroupBox.GroupDirectionEnum.Vertical;
}
parent = Groups.Add(g);
if (boxes.Count > 1){ # 算法继续递归的条件:至少还有两个及以上的组件在子组件列表中
# 记录父容器的位置信息:(x,y)和 宽高
g.X = boxes.Min(p => p.Left); # 找到子组件中最小的横坐标为父容器的横坐标
g.Y = boxes.Min(p => p.Top); # 找到子组件中最小的纵坐标为父容器的纵坐标
g.Width = boxes.Max(p => p.Width);
g.Height = boxes.Max(p => p.Height);
# 生成父组件的片段划分(其划分形似尺子 ruler)
ProjectionRuler ruler = BulidProjectionRuler(boxes, axis);
# 递归子组件列表,其排布方式和父容器不同,后者横向(X)排布,则前者纵向(Y)排布
foreach (Section sec in ruler.Section){
if (axis == ProjectionAxisEnum.X){
BulidChildGroups(sec.Boxes, ProjectionAxisEnum.Y, g);
} else {
BulidChildGroups(sec.Boxes, ProjectionAxisEnum.X, g);
}
}
} else { # 算法终止递归
if (boxes.Count == 0){
g.IsEmpty = true;
}
if (boxes.Count == 1){
g.X = boxes.Min(p => p.Left);
g.Y = boxes.Min(p => p.Top);
g.Width = boxes.Max(p => p.Width);
g.Height = boxes.Max(p => p.Height);
g.Boxes.Add(boxes[0]); # 把子组件加入父容器的子组件列表
CalculateAlignments(g); # 计算父组件内部子组件的对齐方式(左/中/右)
}
}
}
可以看到上面的两个函数描述了算法递归的主流程,在递归里,我们只需要关注父容器的信息,这部分信息是通过求取子组件的最小值坐标(x,y) 和最大值宽高来获得的。
1)当父容器内部没有子组件或只有一个子组件则递归完成,没有子组件则标示IsEmpty为true,有一个子组件则父容器中添加上该子组件到其 Boxes 列表中,并计算该子组件在父容器中的对齐方式,类似 CSS 中的 align 属性有左中右(left/center/right)三个选择。
2)当父容器内部有多余一个组件的时候,递归继续。此时我们需要计算父组件的片段,并将其合并成得到下一层的父容器区域。这部分功能在函数BulidProjectionRuler中实现,我们在下面来介绍具体的运算过程。
2. 设计递归内部父子组件的归类策略:
2.1 根据本层组件的排列方向,在父组件中生成均分的 n 个片段。
2.2 遍历其余组件,将符合条件的子组件加入上面生成的 n 个片段中。
2.3 利用组件间隙(即空白片段)划分区域(合并相邻且不为空的片段),去除片段内重复的子组件,每一个区域成为新的父组件,往其内部寻找其子组件集合(继续递归)。
# 父容器内部归类策略 - 生成标尺(划分区域)
# boxes - 组件列表
# axis - 目前该层父容器内部子组件的排列方向
public ProjectionRuler BuildProjectionRuler(List<BoundingBox> boxes, ProjectionAxisEnum axis){
ProjectionRuler ruler = new ProjectionRuler(); # 空节点,后续添加标尺划分的区域信息
List<SliceSection> slices = buildSlices(boxes, axis); # 2.1 均分片段
fillSlices(boxes, slices, axis); # 2.2 向片段中添加子组件
Section s = new Section(); # 空节点,后续添加划分的片段信息
s.Slices.Add(slices[0]);
ruler.Section.Add(s);
bool isEmpty = false;
# 2.3 根据片段是否为空来划分区域
for (int i = 1; i < slices.Count; i++){
if (!isEmpty){ # 上一个区域 不是 空白区域
if (slices[i].IsEmpty){ # 遇到空白片段
s = new Section(); # 上个区域结束,新的区域开始
s.Slices.Add(slices[i]);
isEmpty = true;
ruler.Section.Add(s);
} else {
s.Slices.Add(slices[i]); # 继续在之前的区域里添加子组件
}
} else { # 上一个区域 是 空白区域
if (!slices[i].IsEmpty){ # 遇到空白片段
s = new Section(); # 上个区域结束,新的区域开始
s.Slices.Add(slices[i]);
isEmpty = false;
ruler.Section.Add(s);
} else {
s.Slices.Add(slices[i]); # 继续在之前的区域里添加子组件
}
}
}
return ruler;
}
从上面的归类策略的函数可以看出,这部分主要是一个归类流程的实现,划分区域的依据就是我们在 2.1 和 2.2 步骤中得出的片段是否为空这个信息。
2.1 根据本层组件的排列方向,在父组件中生成均分的 n 个片段。
# 均分片段
# boxes - 组件列表
# axis - 目前该层父容器内部子组件的排列方向
private static List<SliceSection> buildSlices(List<BoundingBox> boxes, ProjectionAxisEnum axis){
double precision = 1000; # 将父容器划分1000次,即有1001个片段
double min;
double max;
if (axis == ProjectionAxisEnum.Y){ # 纵向划分 y 坐标
min = boxes.Min(p => p.Top);
max = boxes.Max(p => p.Top + p.Height);
} else { # 横向划分 x 坐标
min = boxes.Min(p => p.Left);
max = boxes.Max(p => p.Left + p.Width);
}
double sliceSize = (max - min) / precision; # 每一份片段的长度
List<SliceSection> slices = new List<SliceSection>();
for (double i = min; i < max; i = i + sliceSize){
SliceSection slice = new SliceSection(); # 初始化片段的信息
slice.Start = i;
slice.End = i + sliceSize;
slice.IsEmpty = false;
slices.Add(slice);
}
return slices;
}观察上面的函数,可以知道一个片段需要包含开始和结束的位置信息,以及片段是否为空的信息,在初始化片段的阶段,片段都默认为空。
2.2 遍历其余组件,将符合条件的子组件加入上面生成的 n 个片段中。
# 向片段加入子组件
# boxes - 组件列表
# slices - 片段数组
# axis - 目前该层父容器内部子组件的排列方向
private static void fillSlices(List<BoundingBox> boxes, List<SliceSection> slices, ProjectionAxisEnum axis){
int first;
int last;
foreach (BoundingBox b in boxes){
if (axis == ProjectionAxisEnum.Y){ # 纵向划分 y 坐标
first = slices.FindIndex(p => (p.Start <= b.Top) && (p.End >= b.Top));
last = slices.FindIndex(p => (p.End >= b.Top + b.Height));
} else { # 横向划分 x 坐标
first = slices.FindIndex(p => (p.Start <= b.Left) && (p.End >= b.Left));
last = slices.FindIndex(p => (p.End >= b.Left + b.Width));
}
for (int i = first; i <= last; i++){
slices[i].IsEmpty = false;
slices[i].Boxes.Add(b);
}
}
}片段开始位置的标准为:片段开始位置坐标 <= 组件横/纵坐标 并且 片段结束位置坐标 >= 组件横/纵坐标;片段结束位置的标准为:片段结束位置坐标 >= 组件横/纵坐标 + 组件长/宽(也就是已知顶点的对角顶点坐标)。
得到的片段的开始和结束位置标示了一段片段的范围,在后续的 for 循环中,再将该组件放入这些范围的每一个片段中。这里的 Boxes 属性是作者自定义的,其 get 方法内部已经实现了去除重复 box 的操作。感兴趣的小伙伴可以参考 Section.cs 类定义文件来查看具体的实现。
计算父容器内部子组件的对齐方式
public void CalculateAlignments(GroupBox g){
if (g.Direction == GroupDirectionEnum.Horizontal && g.Boxes.Count == 1){
GroupBox b = g.Boxes[0];
double center_b = (b.Width / 2) + b.Left;
double center_g_steps = b.MaxWidth / 3;
if (center_b < center_g_steps){ # 中心点位于左边的1/3范围内
g.Alignment = GroupBox.GroupAlignmentEnum.Left;
} else { # 中心点位于右边的2/3范围内
if (center_b > center_g_steps & center_b < center_g_steps * 2){ # 中心点位于中间的1/3范围内
g.Alignment = GroupBox.GroupAlignmentEnum.Center;
} else { # 中心点位于右间的1/3范围内
g.Alignment = GroupBox.GroupAlignmentEnum.Right;
}
}
}
}这里的思路是先判断父容器内部的排布方式是否是横向排布的,纵向排布则不做处理。确定是横向排布的父容器后,将其均分成了(左/中/右)三个区域,利用子组件的中心点落入这三个区域的位置,来确定子组件在父容器中的对齐方式(左/中/右)。
我自己用 Python 实现了一个版本:
https://github.com/theforeverhope/data-structure-conversion
直接从 GitHub 里打不开 ipynb 文件的朋友可以参考这个链接打开:
http://nbviewer.jupyter.org/github/theforeverhope/data-structure-conversion/blob/master/data_structure_conversion.ipynb
我使用的原数据结构是 Faster R-CNN 模型识别UI稿结果的简易版本,最后的划分效果用 matplotlib.pyplot 库作图表现了出来,同颜色的部分为划分到同一个层级的子组件。由于内部和外部会有颜色重叠覆盖,所以最后图上的颜色略杂。我将原UI稿图作为背景图绘制在识别结果下方,方便大家对比识别结果的准确度。核心函数命名都是对标了本文的项目代码,所以我实现的版本没有再做过多的注释说明,欢迎参阅我的实践结果,批评和指导 ^-^ 谢谢大家!
算法优化
遗留问题
首先,在上文算法步骤的 2.3 中,我们提到区域的划分是根据不包含任何组件的空白片段来进行的。那么这就遗留了一个问题,如果整个父组件内部的子组件都是相连的,没有任何间隙,甚至位置互相重叠,那么我们将不可区分这些子组件。
再则,递归函数的递归完成条件是:当父容器内部只有一个子组件或没有子组件,则完成递归。然而考虑上述子组件不可分的情况,在横向和纵向都无法分开多于一个的子组件集合会导致递归无限循环无法终止,从而用尽程序空间,导致程序异常退出的情况。
解决方案
1. 我们需要设计一个函数在数据结构变换之前,将所有的 boxes 遍历一遍,把所有重叠的 box 的位置通过左右上下移动和伸缩的方式相互分离开来。
2. 由于父容器划分片段的精度 precision 是人为写死在程序里的,所以上一步需要划分多宽的组件间距,还需要结合UI手稿图片本身的大小(长宽像素值)和这里的片段划分精度来确定。
计算重叠部分面积和比率的函数在 Overlap.cs 文件中实现,具体实施分离位置操作的函数在 Geometry.cs 文件中实现。有兴趣的读者可以自行参阅,为控制篇幅本文就不详细解说了。
我将试着分析这一过程,并提出一点疑问和猜想:
参考作者的示例图片(长1302像素 * 宽1126像素),其划分精度为1000,则大约每1.1~1.3像素的图像会被分到一个片段内。在 Geometry.cs 中的 RemoveOverlappingX 函数中我们看到 TO_MOVE = 50,也就是项目作者将两个重叠的组件相互会移开50像素的距离。这里我有些不太理解这个设定,因为1.1和50的量级差距较大。对此我的猜测是:
1)像素读入程序后的矩阵长度可能和像素的长度会有所不同,导致了这个量级的差距,但是由于需要到官网注册申请 key 才能完整运行并调试这个程序,所以这里的原因我没有继续去探索,未来有了新的发现,会再写作其他的文章进行后续的说明。
2)如果像素长度和读入程序的图片矩阵长度相等,那么在读入图片之后的图片处理过程中可能有对图片进行拉伸或者压缩的操作,来平衡数量级的差距,但是由于程序的其他部分我没有一一阅读分析,这部分只是猜测,读者可以自行取证研究。
我也在自己实现处理重叠部分代码的过程中,发现了一些原项目代码处理不了的异常情况,后续将在自己实现的完成版本中详细解说。
代码生成
准备工作
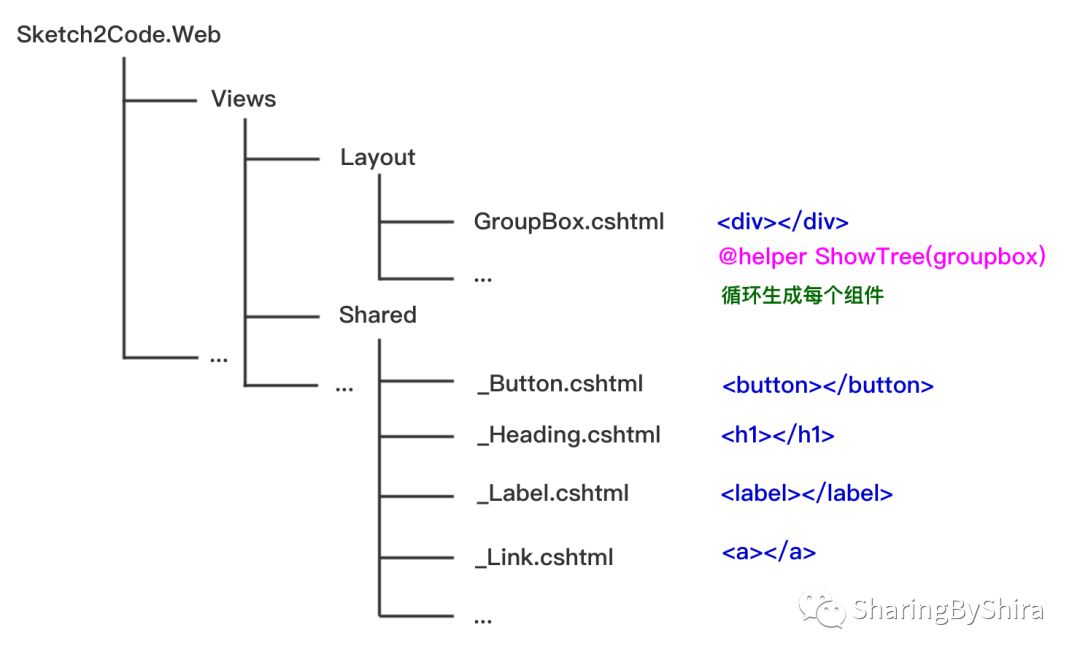
首先需要人为的写入可能的子组件模版,例如常用的 html 元素:button、h1、label、a、img 等等。
代码生成
行业动态
UI2Code - 阿里巴巴
阿里巴巴闲鱼团队介绍了自行研发还未开源的“UI2Code”工程,其与微软已经开源的“Sketch2Code”的区别是:更关注1:1像素级别的精确还原。为了生成可以直接作为上线使用的代码,减少开发人员重复机械的视觉还原工作,从而可以使开发人员更专注于逻辑性的工作。
参考知乎:[阿里云云栖社区] 谷歌开发者大会2018实录 - TensorFlow篇
Shira
从毕业到现在我经历了 android 开发转 php 开发转 前端开发,到如今Python 和前端并重的开发道路。我一直试图去总结不同语言、不同方向的编程的特点和优势,却总感觉经验有限,有点说不清道不明其中原委的无力感。直到看到了本文项目作者的代码,让我有种恍然大悟的感觉,这确实是符合前端思路所实现的前端代码构建过程。基于对于前端组件行为规范的了解,结合可控的CSS排版,作者实现了初步的前端代码生成。再结合UI稿识别服务,进一步提供了从UI稿到前端代码的一步生成服务,对于未来减少重复的视觉还原工作给出了一个具有实际指导意义的范例。
本文写的其实略啰嗦,这样行文的原因是,我想通过这篇文章给那些像我一样,想要阅读源码,却会因为其代码量望而却步的同学们一点思路方面的建议。通过确定自己的核心问题,和划分代码模块功能,我们可以找到自己关心的核心模块,从这里开始摸清程序逻辑,循序渐进的阅读源码,最后学习到其核心思想。
希望机器能让我们从繁重的体力劳动和重复劳动中解脱出来,使我们可以投入到真正的脑力劳动,和更具有逻辑性和创造性的工作中。
以上是关于Sketch2Code 微软:手绘UI稿生成前端代码项目的主要内容,如果未能解决你的问题,请参考以下文章