人工神经网络和BaggingRegressor预测模型比较分析
Posted 数据皮皮侠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工神经网络和BaggingRegressor预测模型比较分析相关的知识,希望对你有一定的参考价值。
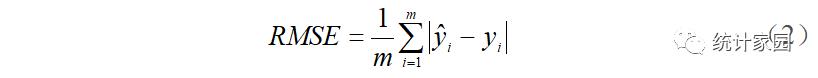

三、实证分析
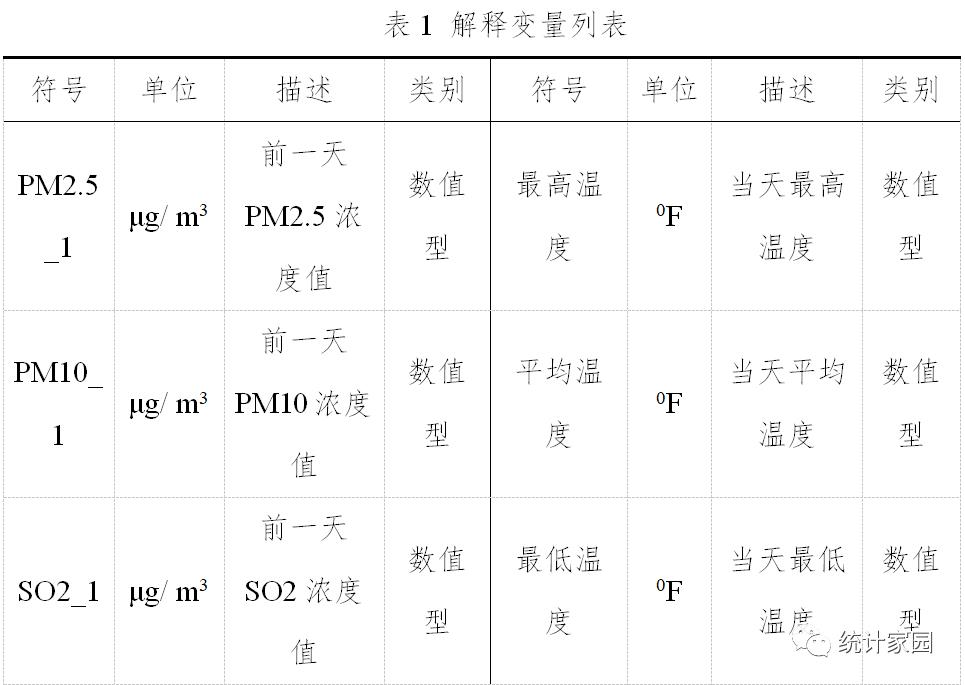
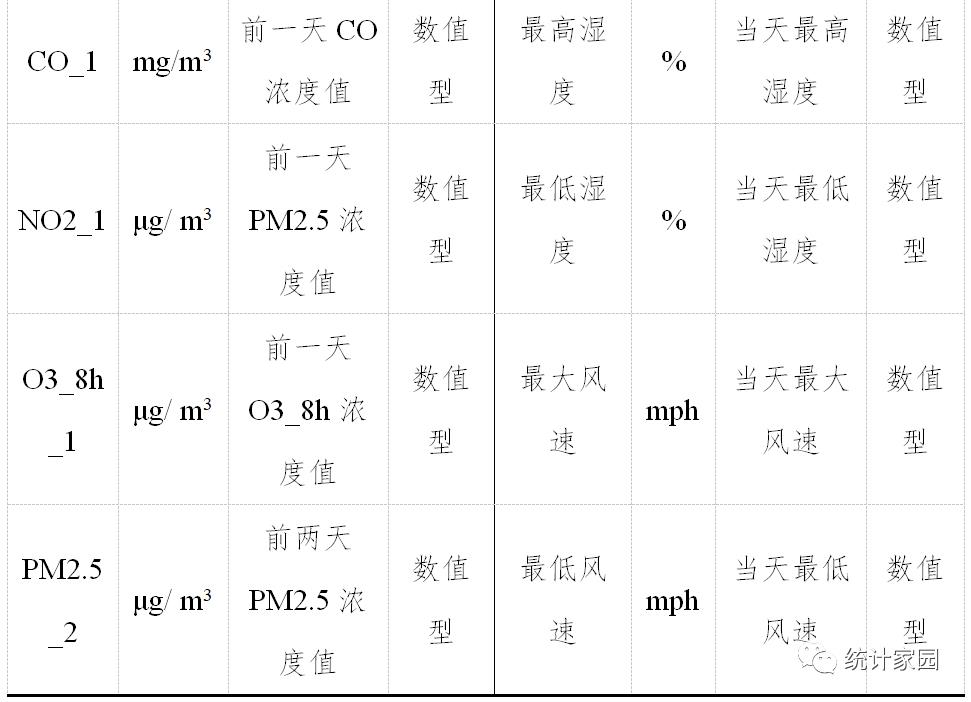
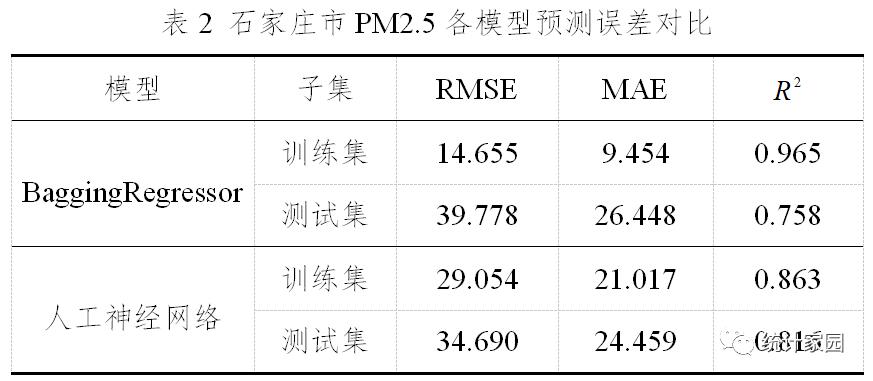
#引入基本包import numpy as npimport pandas as pdimport pylab as mpl#导入中文字体,避免显示乱码#可视化import matplotlibimport matplotlib.pyplot as pltimport seaborn as sns#timefrom datetime import datetimefrom sklearn.model_selection import cross_val_score#读取数据mpl.rcParams['font.sans-serif']=['SimHei'] #设置为黑体字data= pd.read_excel('shijiazhuang_pm25.xlsx',parse_dates=True,index_col=0,encoding = 'utf-8')print(data.shape)#查看是否有缺失值data.isnull().sum()# 缺失数据占比小,删除缺失数据data1=data.dropna(axis=0)print(data1.shapedata1_month=data1.resample('M').mean() #按月重采data1_month['PM2.5'].plot(figsize=(15,4),marker='o'#获取标注,ylabel = np.array(data1['PM2.5'])#获取特征,xfeatures= data1.drop('PM2.5', axis = 1)#保存变量名称feature_list = list(features.columns)# 转化成arrayfeatures = np.array(features)# 划分训练集和测试集from sklearn.model_selection import train_test_splittrain_features, test_features, train_label, test_label = train_test_split(features,label, test_size = 0.2,random_state = 42)print('Training Features Shape:', train_features.shape)print('Training Labels Shape:', train_label.shape)print('Testing Features Shape:', test_features.shape)print('Testing Labels Shape:', test_label.shape)#BaggingRegressorfrom sklearn.ensemble import BaggingRegressorregr = BaggingRegressor(n_estimators=100, oob_score=True, random_state=1010)regr.fit(train_features, train_label);regr_train_predictions= regr.predict(train_features)regr_test_predictions = regr.predict(test_features)print("BaggingRegressor train RMSE:%.3f"%np.sqrt(mean_squared_error(train_label,regr_train_predictions)))print("BaggingRegressor test RMSE:%.3f"%np.sqrt(mean_squared_error(test_label,regr_test_predictions)))print("BaggingRegressor train MAE:%.3f"%mean_absolute_error(train_label,regr_train_predictions))print("BaggingRegressor test MAE:%.3f"%mean_absolute_error(test_label,regr_test_predictions))print(" BaggingRegressor train r2:%.3f"%r2_score(train_label,regr_train_predictions))print(" BaggingRegressor test r2:%.3f"%r2_score(test_label,regr_test_predictions))#神经网络from sklearn.neural_network import MLPRegressormlp=MLPRegressor(solver='lbfgs',hidden_layer_sizes=(100,50),batch_size='auto',alpha=0.01)mlp.fit(train_features, train_label);mlp_train_predictions= mlp.predict(train_features)mlp_test_predictions =mlp.predict(test_features)print("MLPRegressor train RMSE:%.3f"%np.sqrt(mean_squared_error(train_label,mlp_train_predictions)))print("MLPRegressor test RMSE:%.3f"%np.sqrt(mean_squared_error(test_label,mlp_test_predictions)))print("MLPRegressor train MAE:%.3f"%mean_absolute_error(train_label,mlp_train_predictions))print("MLPRegressor test MAE:%.3f"%mean_absolute_error(test_label,mlp_test_predictions))print("MLPRegressor train r2:%.3f"%r2_score(train_label,mlp_train_predictions))print("MLPRegressor test r2:%.3f"%r2_score(test_label,mlp_test_predictions))#神经网络在测试集上表现效果最好#神经网络预测值和实际值比较import pylabpylab.rcParams['figure.figsize'] = (15,4) #显示大小plt.plot(test_label, 'bo-', label = '真实值')plt.plot(mlp_test_predictions, 'ro', label = '预测值')plt.xticks(rotation = '60');plt.legend()plt.ylabel('PM2.5')
以上是关于人工神经网络和BaggingRegressor预测模型比较分析的主要内容,如果未能解决你的问题,请参考以下文章