动手实现神经网络

Posted 2021-04-26 程序员干货铺

一个帮助初学者理解深度神经网络内部工作机制的指南

写作动机： 为了使我自己可以更好地理解深度学习，我决定在没有像 TensorFlow 这样的深度学习库的情况下，从零开始构建一个神经网络。我相信，理解神经网络的内部工作原理对任何有追求的数据科学家来说都很重要。

这篇文章包含了我所学到的东西，希望对你们也有用。

什么是神经网络？

大多数介绍神经网络的文章在描述它们时都会与大脑做类比。在不深入研究与大脑类似之处的情况下，我发现将神经网络简单地描述为给定输入映射到期望输出的数学函数更容易理解一些。

神经网络由以下几个部分组成：

•一个输入层，x•任意数量的隐含层•一个输出层，ŷ•层与层之间的一组权重和偏差，W 和 b•每个隐含层中所包含的一个可选的激活函数，σ。在本教程中，我们将使用 Sigmoid 激活函数。

下图展示了 2 层神经网络的架构（注：在计算神经网络中的层数时，输入层通常被排除在外）

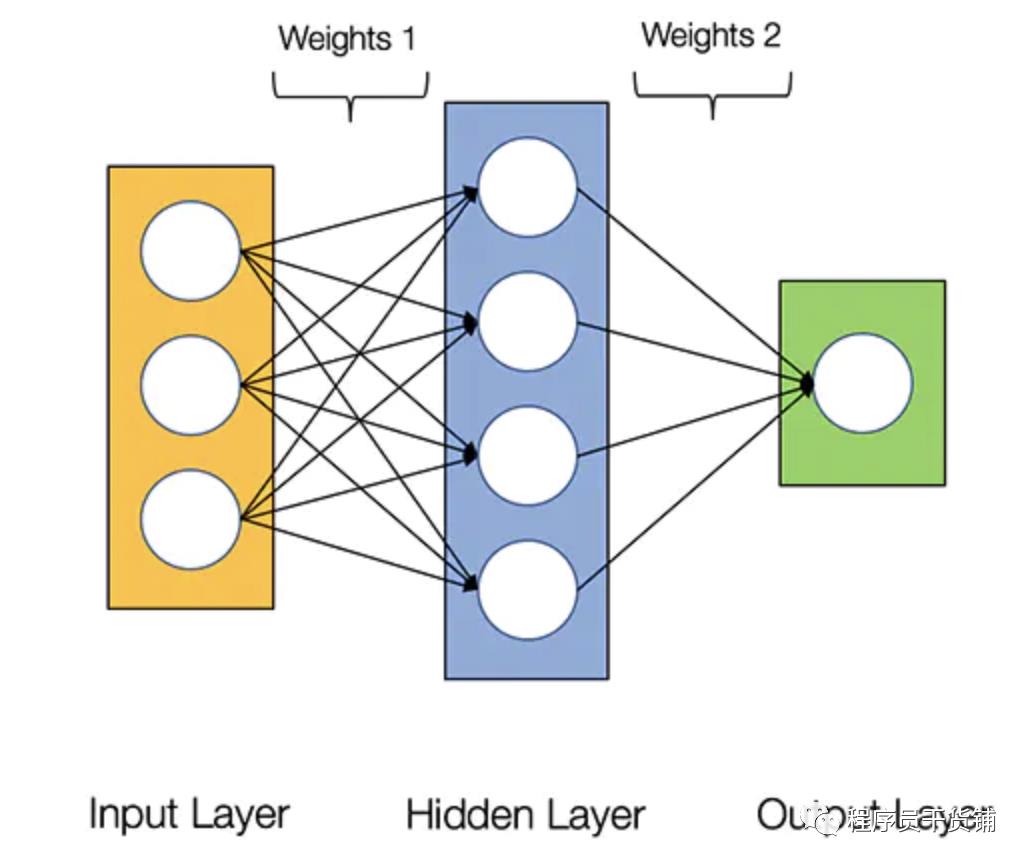
2 层神经网络的架构

在 Python 中创建一个神经网络的类很简单。

class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4)  self.weights2 = np.random.rand(4,1)  self.y = y self.output = np.zeros(y.shape)

训练神经网络

一个简单的 2 层神经网络的输出 ŷ\ 如下：

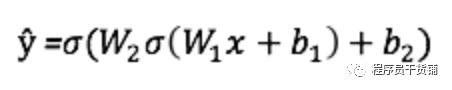
你可能注意到了，在上面的等式中，只有权重 W\ 和偏差 b\ 这两个变量会对输出 ŷ\ 产生影响。

当然，合理的权重和偏差会决定预测的准确程度。将针对输入数据的权重和偏差进行微调的过程就是训练神经网络的过程。

训练过程的每次迭代包括以下步骤：

•计算预测输出的值 ŷ\，即前馈•更新权重和偏差，即反向传播

下面的序列图展示了这个过程。

前馈过程

正如我们在上面的序列图中看到的，前馈只是一个简单的计算过程，对于一个基本的 2 层神经网络，它的输出是：

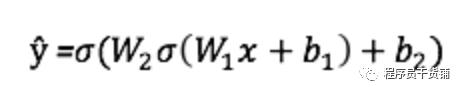
让我们在 Python 代码中添加一个前馈函数来实现这一点。注意，为了简单起见，我们假设偏差为 0。

class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4)  self.weights2 = np.random.rand(4,1)  self.y = y self.output = np.zeros(self.y.shape)
 def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2))

但是，我们仍然需要一种方法来评估预测的“精准程度”（即我们的预测有多好）？而损失函数能让我们做到这一点。

损失函数

可用的损失函数有很多，而我们对损失函数的选择应该由问题本身的性质决定。在本教程中，我们将使用简单的平方和误差作为我们的损失函数。

这就是说，平方和误差只是每个预测值与实际值之差的总和。我们将差值平方后再计算，以便我们评估误差的绝对值。

训练的目标是找到能使损失函数最小化的一组最优的权值和偏差。

反向传播过程

现在我们已经得出了预测的误差（损失），我们还需要找到一种方法将误差传播回来，并更新我们的权重和偏差。

为了得出调整权重和偏差的合适的量，我们需要计算损失函数对于权重和偏差的导数。

回忆一下微积分的知识，计算函数的导数就是计算函数的斜率。

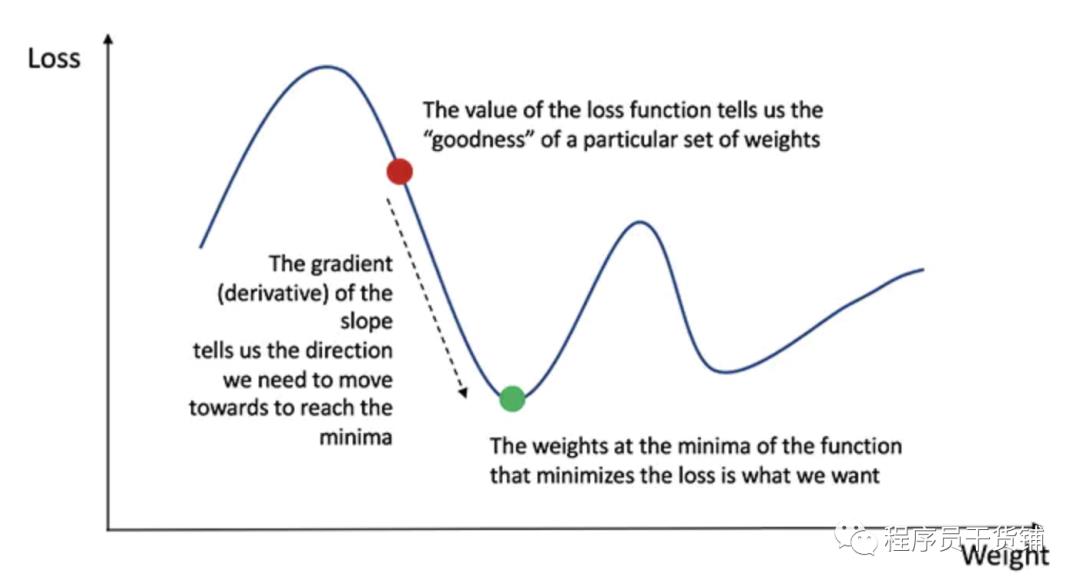
梯度下降算法

如果我们已经算出了导数，我们就可以简单地通过增大/减小导数来更新权重和偏差（参见上图）。这就是所谓的梯度下降。

然而，我们无法直接计算损失函数对于权重和偏差的导数，因为损失函数的等式中不包含权重和偏差。因此，我们需要链式法则来帮助我们进行计算。

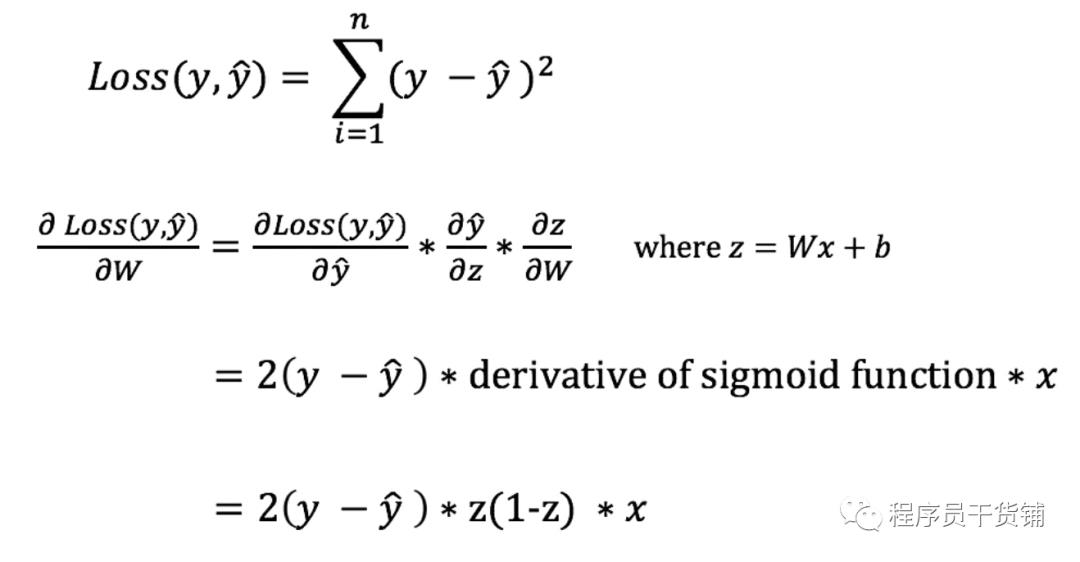
为了更新权重使用链式法则求解函数的导数。注意，为了简单起见，我们只展示了假设为 1 层的神经网络的偏导数。

哦！这真难看，但它让我们得到了我们需要的东西 —— 损失函数对于权重的导数（斜率），这样我们就可以相应地调整权重。

现在我们知道要怎么做了，让我们向 Pyhton 代码中添加反向传播函数。

class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4)  self.weights2 = np.random.rand(4,1)  self.y = y self.output = np.zeros(self.y.shape)
 def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2))
 def backprop(self): # 应用链式法则求出损失函数对于 weights2 和 weights1 的导数 d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output))) d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))
 # 用损失函数的导数(斜率)更新权重 self.weights1 += d_weights1 self.weights2 += d_weights2

如果你需要更深入地理解微积分和链式法则在反向传播中的应用，我强烈推荐 3Blue1Brown 的教程。

融会贯通

现在我们已经有了前馈和反向传播的完整 Python 代码，让我们将神经网络应用到一个示例中，看看效果如何。

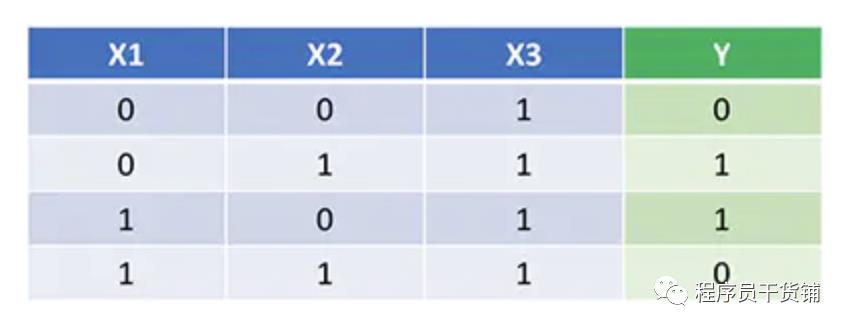
我们的神经网络应该通过学习得出一组理想的权重来表示这个函数。请注意，仅仅是求解权重的过程对我们来说也并不简单。

让我们对神经网络进行 1500 次训练迭代，看看会发生什么。观察下图中每次迭代的损失变化，我们可以清楚地看到损失单调递减至最小值。这与我们前面讨论的梯度下降算法是一致的。

让我们看一下经过 1500 次迭代后神经网络的最终预测（输出）。

1500 次训练迭代后的预测结果

我们成功了！我们的前馈和反向传播算法成功地训练了神经网络，预测结果收敛于真实值。

请注意，预测值和实际值之间会存在细微的偏差。我们需要这种偏差，因为它可以防止过拟合，并允许神经网络更好地推广至不可见数据中。

后续的学习任务

幸运的是，我们的学习旅程还未结束。关于神经网络和深度学习，我们还有很多内容需要学习。例如：

•除了 Sigmoid 函数，我们还可以使用哪些激活函数？•在训练神经网络时使用学习率•使用卷积进行图像分类任务

我将会就这些主题编写更多内容，请在 Medium 上关注我并留意更新！

结语

当然，我也在从零开始编写我自己的神经网络的过程中学到了很多。

虽然像 TensorFlow 和 Keras 这样的深度学习库使得构建深度神经网络变得很简单，即使你不完全理解神经网络内部工作原理也没关系，但是我发现对于有追求的数据科学家来说，深入理解神经网络是很有好处的。

这个练习花费了我大量的时间，我希望它对你们也有帮助！