支持向量机原理推导

Posted 2021-04-26 Python中文社区

專 欄

❈

exploit，Python中文社区专栏作者。希望与作者交流或者对文章有任何疑问的可以与作者联系：

当前浏览器不支持播放音乐或语音，请在微信或其他浏览器中播放

❈

用python进行数据挖掘和机器学习一直很火，所以近段时间就在自学《机器学习实战》这本书，发现里面讲支持向量机时对原理公式的推导讲得并不详细，上网查资料发现讲得并不很系统，有点零碎的感觉，导致对于我这种小白的童鞋来说颇为艰难，因此经过长时间的资料查询后准备综合各路大神的思路和我自己的理解来写一波关于公式原理推导的文章。文章以《机器学习实战书》为进度进行步步拆解（大神可以略过啦~正在奋斗的小白也可以私下交流共同学习）。 
SVM指的是支持向量机(外文名Support Vector Machine)，在机器学习领域，是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。 
我们这里以二维图线性分类为例进行讲解，在对如下图A进行分类时,可得到很多个分割超平面，然而我们要从中选择最优的分割超平面，这便是SVM的要做的，选出最优的分割超平面。

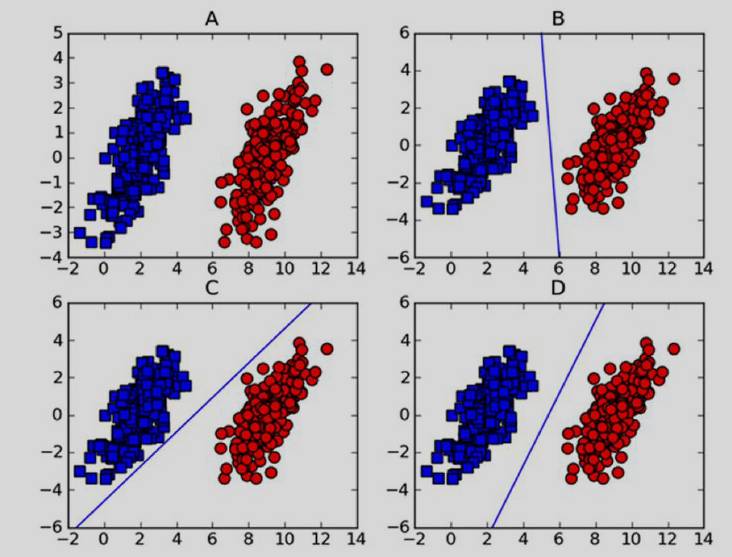
那么什么样的平面为最优的分割超平面呢？就像上图D一样，使距离分割超平面最近的点与超平面的间隔最大便是我们要寻找的，这里距离分割线最近的点就叫做支持向量，分割线就叫做分割超平面，支持向量与分割超平面就叫做”间隔”。我们所要做的就是最大化这个间隔。

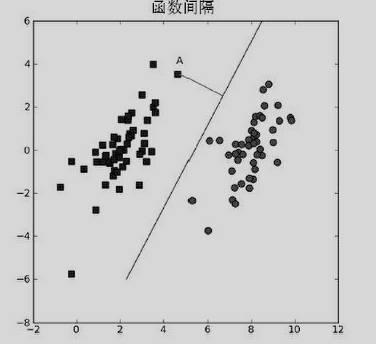
书上给出坐标点A与分割超平面W^tX+b=0间隔的公式为:m=|W^t A+b|/||W|| 
其中W为分割线的系数向量，X为参数向量（此处代表x1,x2）,A为A点的坐标向量。 
那么我们现在就推导一下这个公式。

一、首先我们得简单推导一下坐标点A到过原点直线L的距离。我们有过原点的直线L:W^tX=0(它的法向量为W)，坐标向量A，求A向量在W向量上投影P向量的模长(即A点到直线L的距离)

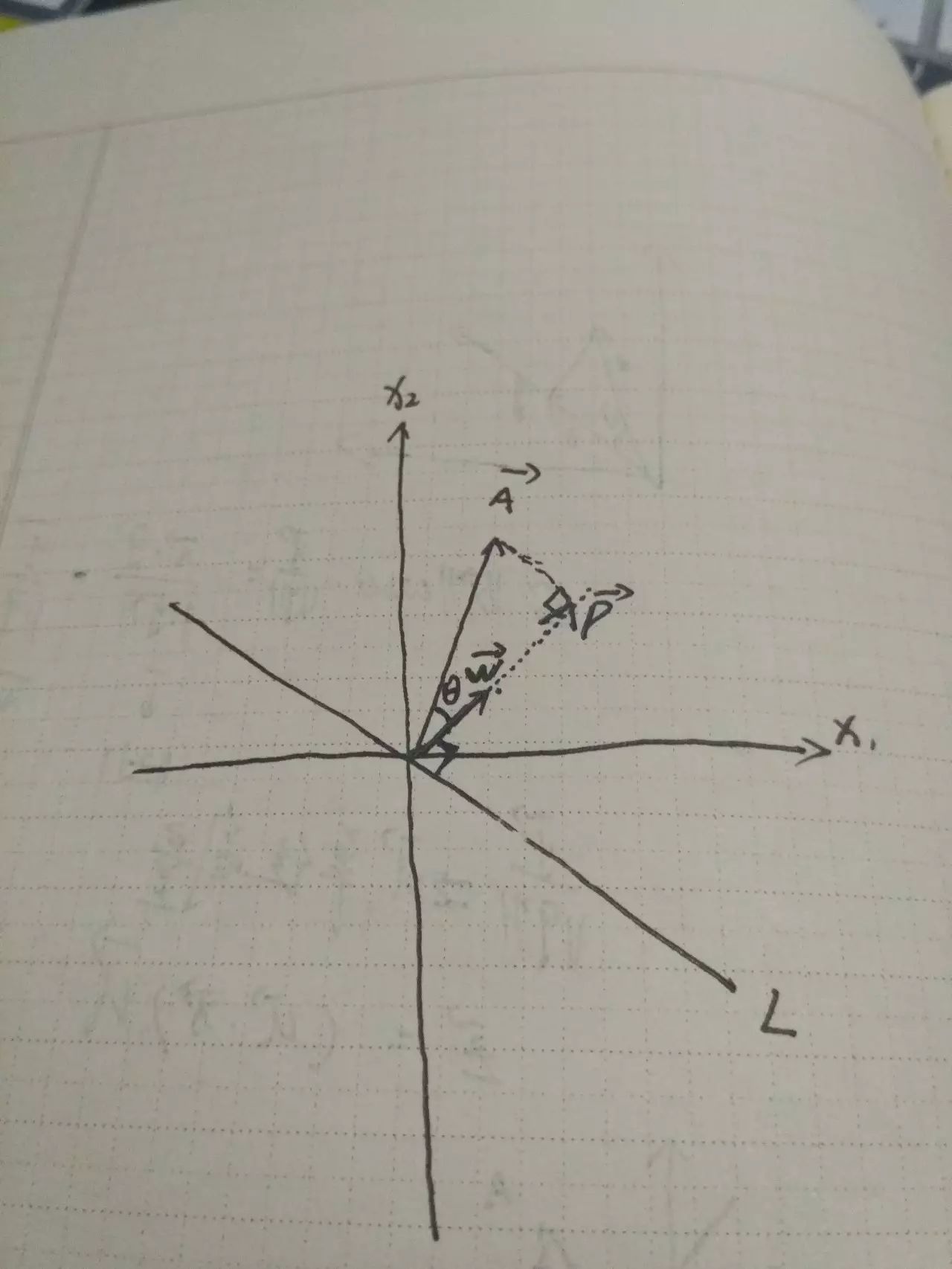
W的方向向量u为u=W/(||W||)，其中||W||代表W向量的模长,||u||=1。 
P的模长|(|P| )|=|(|A| )|cosθ（1） 
又因为u•A=||u||||A||*cosθ=|(|A| )|*cosθ（2） 
由（1）,（2）可得||P||=u•A=(W•A)/(||W||)

二、下面我们推导一下A点到不过原点的直线L的距离：我们有直线L:W^tX+b=0,坐标向量A。

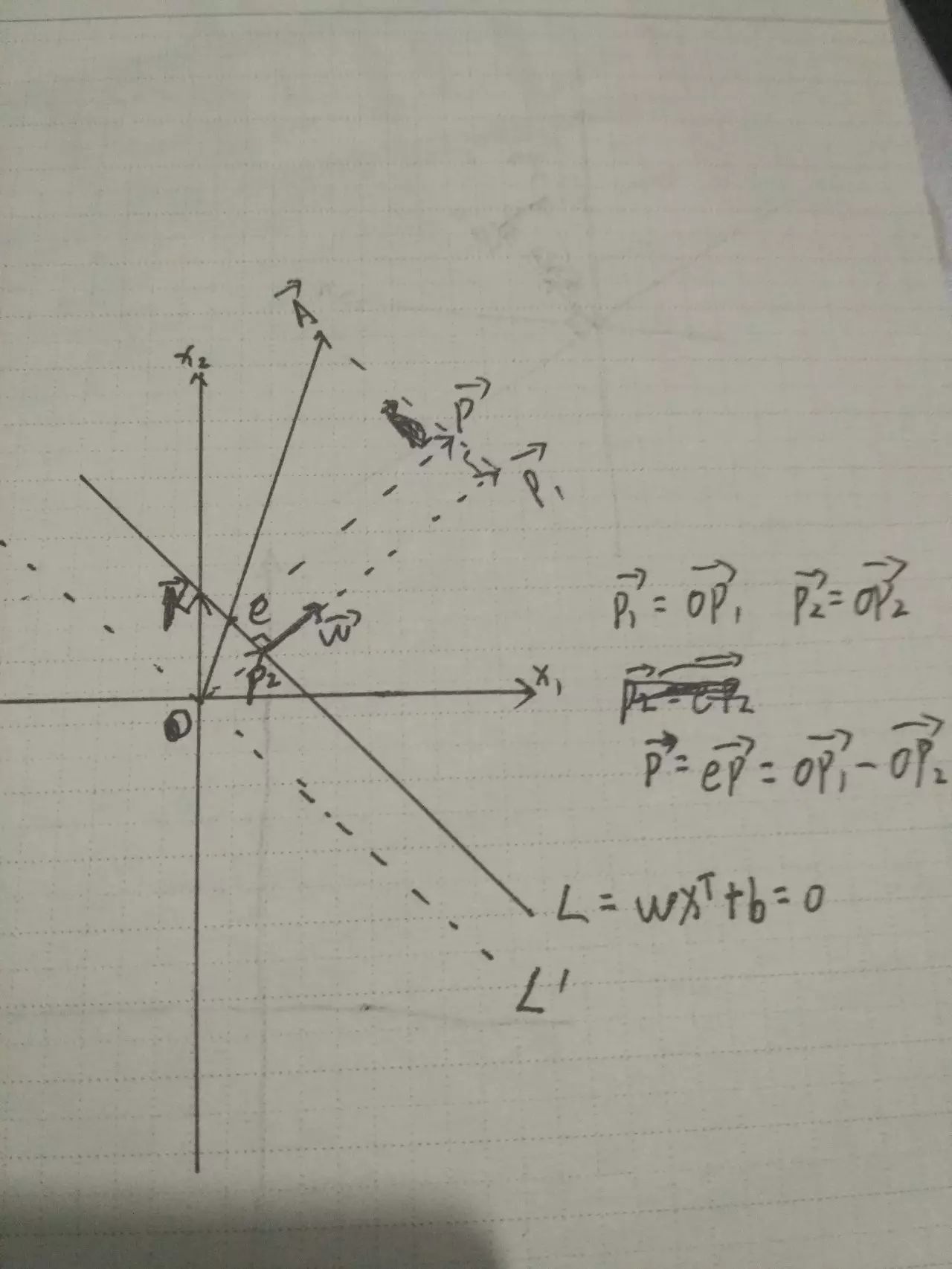
设W(m,n)，X(x1,x2)，直线L为m*x1+n*x2+b=0，截距-b/n，K向量为(0, - b/n) 
所以根据上一条结论可得 
||P2||=(W•K)/(||W||)=((0,(-b)⁄n)•(m,n))/(||W||)=(-b)/(||W||) 
||P2||=(W•A)/(||W||) 
||P||=||P2||-||P2||=(W•A)/(||W||)-(-b)/|(|W| )| =(W•A+b)/(||W||) 
所以间隔 m=|W^t A+b|/||W||

---

长按扫描关注Python中文社区，

获取更多技术干货！

    

Python 中 文 社 区

Python中文开发者的精神家园

合作、投稿请联系微信：

pythonpost

— 人生苦短，我用Python —
1MEwnaxmMz7BPTYzBdj751DPyHWikNoeFS

本文为作者原创作品，未经作者授权同意禁止转载

本社区计划在北京、上海、深圳、广州、香港、杭州、成都、南京、武汉、西安十座城市设立城市俱乐部，以方便同城的Python开发者进行更加深入的交流，同时也为方便以后举办线上线下的活动，欢迎大家加入！ 请直接添加工作人员微信：pythonpost并注明所在城市申请即可。