支持向量机简介

Posted 2021-04-26 信和研究院

数据挖掘一般是指从大量的数据中通过算法搜索隐藏于其中信息的过程。数据挖掘通常与计算机科学有关，并通过统计、在线分析处理、情报检索、机器学习、专家系统和模式识别等诸多方法来实现上述目标。数据挖掘有十大经典算法，支持向量机（Support Vector Machines）便是其中之一。

SVM是建立在统计学习理论的VC维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折中，以求获得最好的推广能力。是一种监督式学习的方法，广泛应用于统计分类及回归分析中。实际应用中，SVM主要用来处理分类问题。迄今为止，已有很多学者写过关于SVM算法的文章，本文仅是抛砖引玉，为初学者做简单介绍，详细推算过程需要读者自行演算。

一、线性可分

SVM最初只是解决二分类的线性分类器，在 n 维的数据空间中找到一个超平面，其方程可以表示为：

分类标准起源于logistic回归， Logistic回归目的是从特征学习出一个0/1分类模型，使用结果标签y=-1和y=1，替换在logistic回归中使用的y=0和y=1。

令分类函数为：

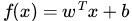
显然，如果 f(x)=0 ，那么 x 是位于超平面上的点。假设对于所有满足 f(x)<0 的点，其对应的 y = -1 ，而 f(x)>0 则对应 y=1 的数据点。

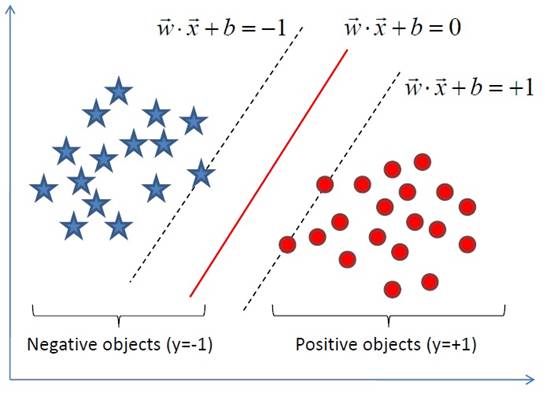
SVM的目标即是找出最大超平面，使两类尽可能的区分开，因此可以把最大间隔问题，转化为求变量和的凸二次规划问题。即：

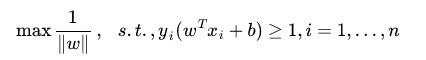
通过求解这个问题，我们就可以找到一个最大的分界面。应用拉格朗日对偶性，通过求解对偶问题得到最优解。给每一个约束条件加上一个 Lagrange multiplier(拉格朗日乘值)，即引入拉格朗日对偶变量，如此我们便可以通过拉格朗日函数将约束条件融和到目标函数里去。

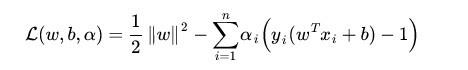
目标函数变成了：

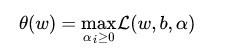
这里用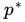表示这个问题的最优值，这个问题和我们最初的问题是等价的。不过，现在我们来把最小和最大的位置交换一下：

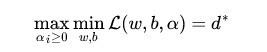
当然，交换以后的问题不再等价于原问题，这个新问题的最优值用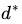来表示。并且，我们有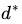≤ 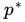，即最大值中最小的一个总也比最小值中最大的一个要大。  总之，第二个问题的最优值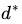在这里提供了一个第一个问题的最优值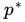

的一个下界，在满足某些条件的情况下，这两者相等，这个时候我们就可以通过求解第二个问题来间接地求解第一个问题。

 这里所说的“满足某些条件”就是要满足KKT条件，即一个最优化数学模型能够表示成下列标准形式：

        

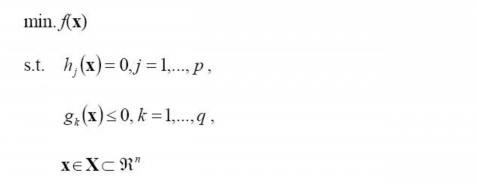
    所谓 Karush-Kuhn-Tucker 最优化条件，就是指上式的最小点 x* 必须满足下面的条件：

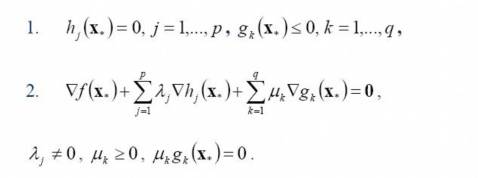
求解这个对偶学习问题，分为3个步骤，首先要让L(w，b，a) 关于 w 和 b 最小化，然后求对α的极大，最后利用SMO算法求解对偶因子。

二、线性不可分

SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也叫惩罚变量）和核函数技术来实现。

我们得到 

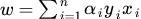
分类函数为：

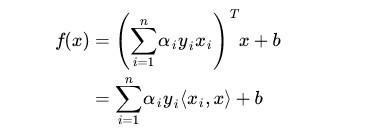
  对于新点 x的预测，只需要计算它与训练数据点的内积即可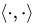（表示向量内积）。对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。通过使用恰当的核函数来替代内积，可以隐式得将非线性的训练数据映射到高维空间。

实际中，我们会经常遇到线性不可分的样例，常用做法是把样例特征映射到高维空间中去，如果一律映射到高维空间，则这个维度大小是会高到可怕的。因此，核函数就起到至关重要的作用了。核函数的价值在于它虽然也是讲特征进行从低维到高维的转换，但它却事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就避免了直接在高维空间中的复杂计算。

常用的核函数有：多项式核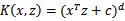

高斯核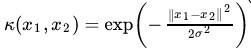

线性核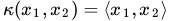

在理解原理的基础上，有兴趣的读者可以动手推导一番，并编程实现。现在网上也有许多现成的代码供参考，希望大家在理解原理的情况下，结合业务需要有参考的使用。