[机器学习与scikit-learn-34]:算法-分类-支持向量机SVM的基本简介与基本原理-线性分类
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[机器学习与scikit-learn-34]:算法-分类-支持向量机SVM的基本简介与基本原理-线性分类相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123778715
目录
4.1 Hard margin面临的困难与soft margin的几何图形
4.3 Soft margin的数学表达式=》把现实问题转换最优化问题
4.4 soft margin的参数求解:最优化求解过程=》梯度下降。
第1章 支持向量机概述
1.1 什么是支持向量机
支持向量机SVM(Support Vector Machine),是机器学习中获得关注最多的算法,是scikit-learn中功能最全面的机器学习算法,没有之一。
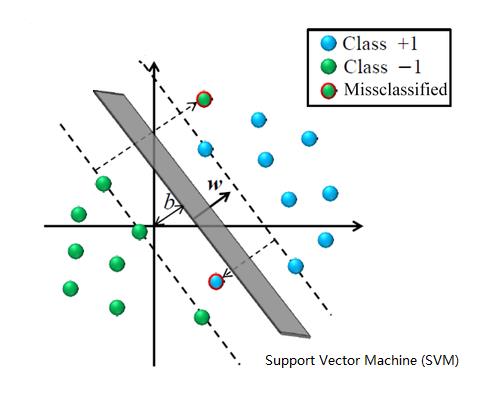
它是利用1个决策边界(二维直线或三维平面)和2个支撑边界(二维直线或三维平面)共同协作,完成对线性和非线性数据的分类, 以及线性与线性数据的拟合。
在上图中,实线称为决策或分类边界线,2个虚线称为支撑边界。
1.2 为什么称为支持向量机
支持向量机=》“支持”、“向量”、“机”,这3个词。
“机”:机器,机器自动完成某种算法功能。
向量:是指样本,每个样本都是多维数据,因此称为向量。
那什么是“支持/支撑”向量呢?也就是说,并非所有的向量都可以称为支持向量。
在支持向量机中,一定存在这样的向量点,它们离决策边界线的距离最近,通过这些点,可以画出2个平行于决策边界线的平行线,这2个平行线就是支撑线(在上图中的虚线部分),用于隔离不同类型的数据。在左侧虚线的上方是一类数据,在右侧虚线的下方的数据就是另一类数据。而虚线的中间是没有数据的。虚线通过的点,称为支持/支撑向量!!!
这就是支持向量机名称的由来!!!。
1.3 支持向量机功能的强大
支持向量机能够完成线性分类、线性拟合、非线性分类、非线性拟合、无监督学习等。

上面的这些功能,基本上通过支持向量机都可以完成。
- 线性分类:Linear SVC
- 线性拟合: Linear SVR
- 非线性分类: SVC
- 非线性拟合: SVR
- 其他: SVM.......
1.4 支持向量机性能的强大
SVM不仅仅功能强大,性能还很优越。
在相同的数据集上,支持向量机RBF SVM的性能在各种功能上,性能都超过决策树、随机深林、AdaBoorst和朴素贝叶斯。
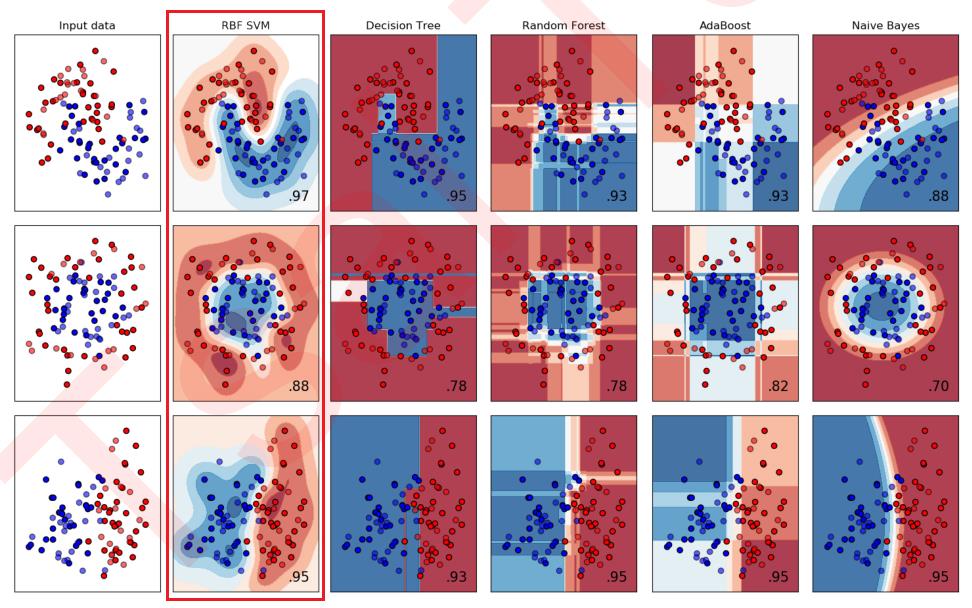
1.5 支持向量机应用广泛
从实际应用来看,SVM在各种实际问题中都表现非常优秀。
它在手写识别数字和人脸识别中应用广泛,在文本和超文本的分类中举足轻重,因为SVM可以大量减少标准归纳(standard inductive)和转换设置(transductivesettings)中对标记训练实例的需求。
同时,SVM也被用来执行图像的分类,并用于图像分割系统。实验结果表明,在仅仅三到四轮相关反馈之后,SVM就能实现比传统的查询细化方案(query refinement schemes)高出一大截的搜索精度。
除此之外,生物学和许多其他科学都是SVM的青睐者,SVM现在已经广泛被用于蛋白质分类,现在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中,人们还使用支持向量机来识别用于模型预测的各种特征,以找出各种基因表现结果的影响因素。
1.6 SVM是最接近深度学习的机器学习算法。
(1)相似点(网络结构相似)
线性SVM可以看成是神经网络的单个神经元
非线性的SVM则与两层的神经网络相当,非线性的SVM中如果添加多个核函数,则可以模仿多层的神经网络。
而从数学的角度来看,SVM的数学原理是公认的对初学者来说难于上青天的水平,对于没有数学基础和数学逻辑熏陶的人来说,探究SVM的数学原理本身宛如在知识的荒原上跋涉。
(2)不同点(网络的使用不同)
- 损失函数不同
- 网络的输出含义不同
第2章 支持向量机的基本思想(以平面二分类为例)
2.1 分类目标与基本思想
数据符合上述分布,如何进行分类了?很多方法可以实现上述目标的分类: 决策树、随机森林,贝叶斯分类,它们通过一个决策边界把两个的数据分开。

2.2 不适宜问题
通过直线边界进行分类问题:在现有样本一定的情况下,中间可分的直线很多种,虽然这些直线在测试样本上,都可以保证测试数据分布在直线的两端,但如何确保决策边界的泛化能力比较好呢?

对边界线的不同的界定方案或方法,即不同的不适应问题的解决办法,就衍生出不同的算法。
(1)普通的逻辑回归与神经网络的基本思想

逻辑回归数据分为0和1,并通过sigmod函数(这是核心)把样本点到直线的距离转换成【0,1】之间的数值。
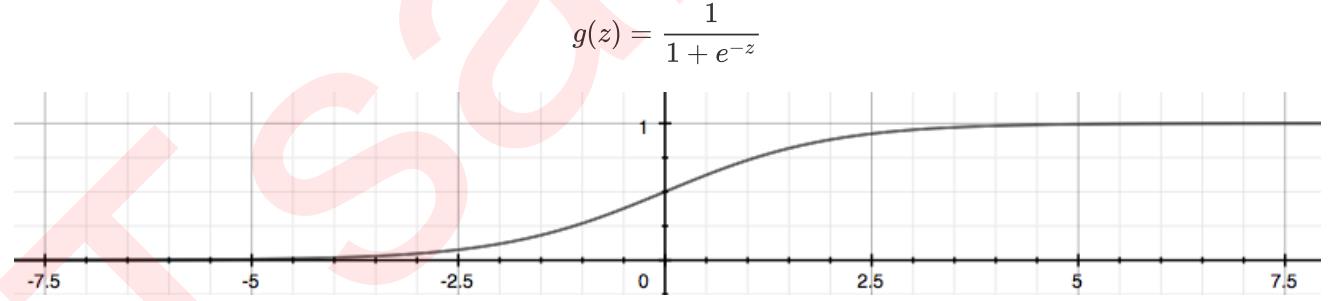
转换后的效果:
- 直线下方离直线的的距离越远,经过sigmod转换后的Ypred数值越接近于0,越接近该类样本的标签值0.
- 直线上方离直线的的距离越远,经过sigmod转换后的Ypred数值越接近于1,越接近该类样本的标签值1.
- 越靠近直线,经过simod转换后,数值越模糊,接近于0.5.
- 下方数据的标签定义为0, 上方数据标签定义为1.
Loss函数与最优化
- 每个样本点到拟合函数的距离Ypred 与标签Yi的差,即是样本的loss = |Ypred - Yi| 或 (Ypred - Yi)^2.
- Loss函数:目标就是所有样本的loss之和最小,
- 最优化:找到合适的直线,使得上述的loss最小,loss最优化问题,找到合适的a,b。使得尽可能多的点离直线的距离远,即 |Ypred - Yi|尽可能接近0.
(2)支持向量机
支持向量机,并没有经过sigmod函数转换,它采用了根据直观的、更加直接、更加简单的方法来分离标签数据。
2.3 支持向量机的基本思想

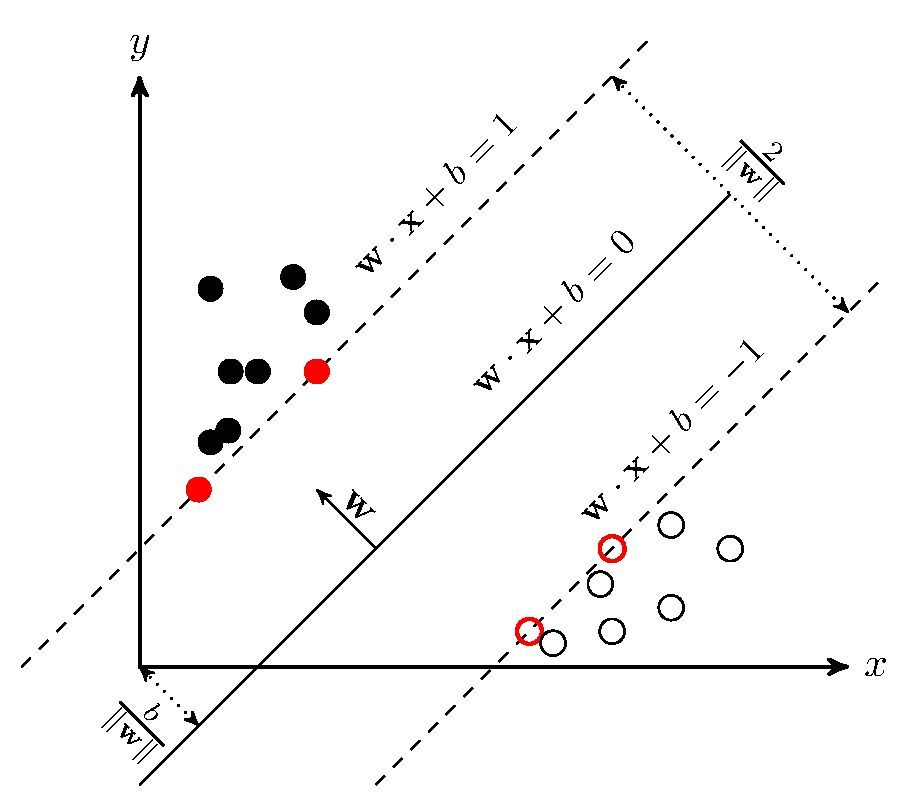
支持向量机并没有采用什么sigmod函数,对样本点到直线的距离进行映射,而直接采用了原始的距离,在上图中,支持向量机定义了新的名称:
(1)定义了3条直线

0号直线:
它能够将样本数据完全分开,这个直线称为决策边界线(隔离线),用 y = wx + b表示,也可以用 wx - y + b = 0表示。
1号直线:
在红色样本点中,存在这样的样本点,它离直线的距离最近,这样的点称为支持向量点。
1号直线就会穿过支持向量点,且1号直线平行于决策边界线,距离为d。
-1号直线:
在蓝色样本点中,存在这样的样本点,它离直线的距离最近,这样的点称为支持向量点。
-1号直线就会穿过支持向量点,且-1号直线也平行于决策边界线,距离为d。
平行:三条直线平行,构成隔离带
(2)定义支撑向量/支持向量点到直线的距离d
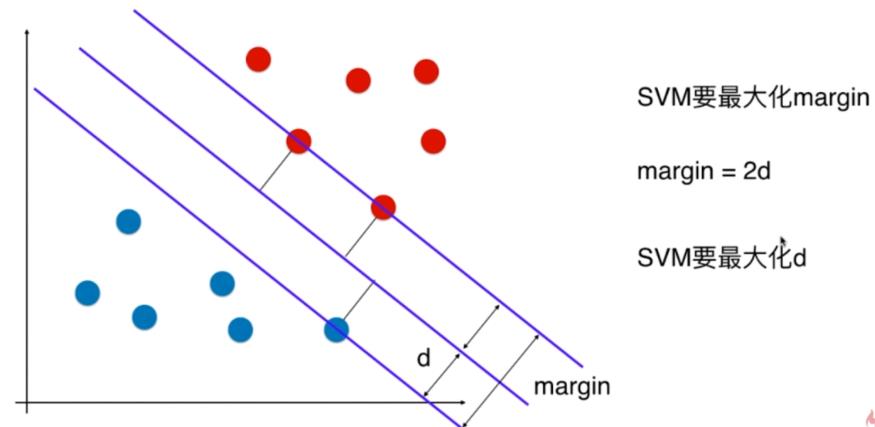
(3)margin:样本点之间的矩形(线性)隔离带
- margin = 2*d
- 支持向量机的目标:就是找到一个直线,使得margin尽可能的大。
上述就是支持向量机的基本思想,
margin越大,样本点之间的矩形(线性)隔离带空间越多,决策边界的隔离效果越好。
当满足上述条件的margin最大时的决策线wx - y + b = 0,就是要找的直线,对应的w,b的参数就是根据模型训练的参数。
提示:
我们可以发现,参数w、b的参数值,与总的样本点数量无关,只与靠近直线最近的样本点相关!!!
支持向量机,只需要少量的典型的样本点,就可以进行学习。
2.4 支持向量机基于思想的进一步说明
(1)隔离带Margin不仅仅要考虑了现在(训练集),还考虑了未来(测试集)
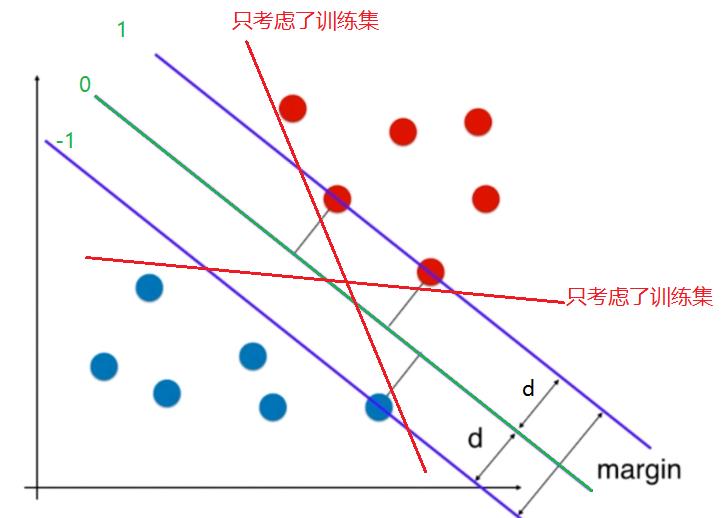
离隔离带Margin边界越近,越容易混淆,类别越模糊,越容易出错。
离隔离带Margin边界越远,类别越明确,确定性越好。
隔离带Margin的所围成的面积越大越好(而不是越小越好)
在上述的探讨中个,隔离带Margin中间是没有样本数据点的,所有的样本数据分布隔离带的两边,这样的隔离带称为:Hard Margin SVM.
第3章 隔离带Hard Margin的数学表达式与最优化
3.1 Hard margin的几何图形
(1)Hard margin的几何图形
(2)点到直线的距离公式
点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。


3.2 Hard margin的数学表达式=》把现实问题转换最优化问题
(1)决策边界线的数学表达式
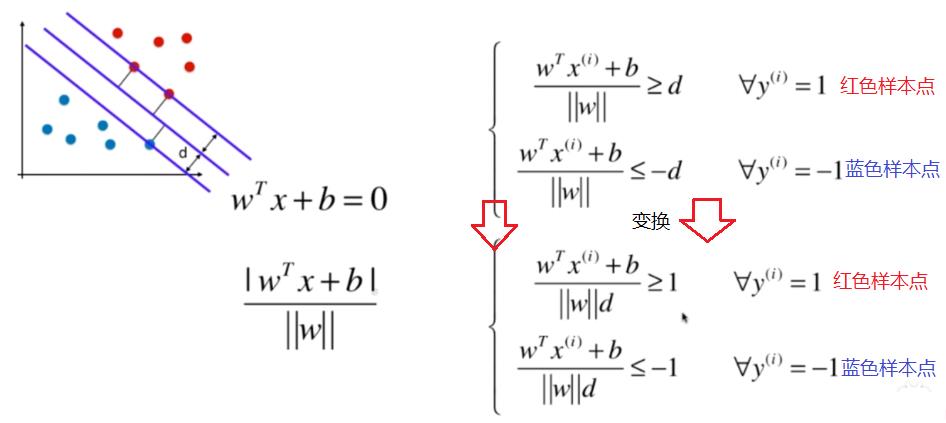
消去常数分母得到:


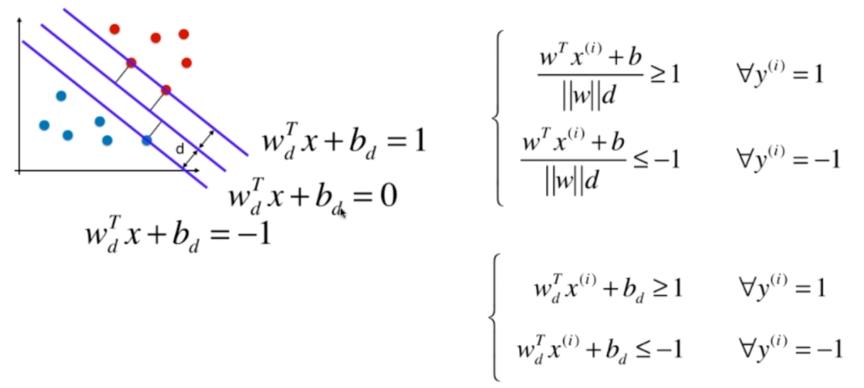
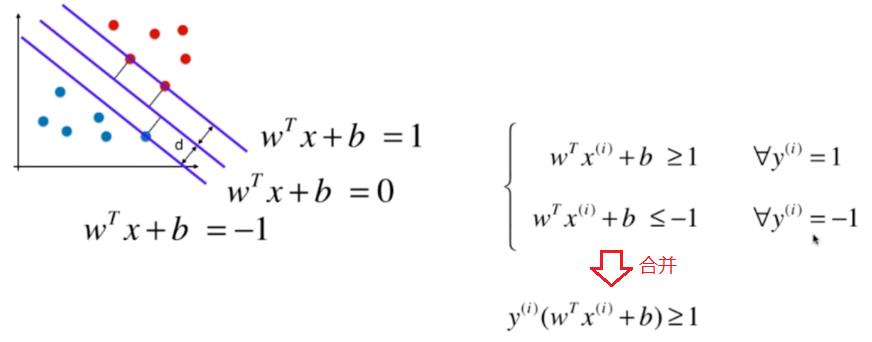
(2)定义最小化目标

由于margin的上下边界线会穿过支撑向量,因此|WX+B|的值=1.
因此,我们的直线的参数满足如下条件:
对于支撑向量点:
直线|WX+B| = 1
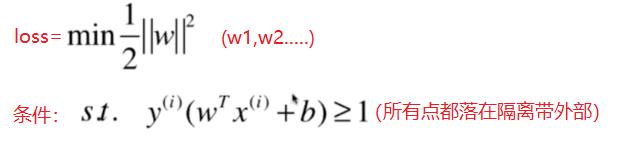
3.3 Hard margin的参数求解:最优化求解过程
这是有有条件下的最优化数值求解,即有条件下求loss函数最小化问题,需要用到拉普拉斯变换。
本文不做进一步的探讨。
但一定能够找到这样的一个W权重向量,使得WX+B =0构建的margin最大,且要确保所有的样本点都落在margin外部(这个限制条件非常重要,这是SVC的重点与难点,也是SVC相对于梯度下降法最重的特点)
第4章 Soft margin SVC的基本原理
4.1 Hard margin面临的困难与soft margin的几何图形

如果按照Hard margin的判断规则,找到一个中间严格不包含任何任何数据点的隔离带的话,会导致两类数据之间边界处的误差较大的点,对最终的结果产生较大的影响。
Hard margin算法求W,B参数时,最主要的依赖是离决策边界最近的点,其中最重要的就是支持向量点,而不是所有的样本的点,通过W,B参数的调整,找到一个直线,使得支持向量点到决策边界线的距离最短。
这种算法效率高,但缺点和尴尬也是很明显的:
越是中间的点,出错的可能性就越大,越是中间的点,误差的可能性就越大,我们完全依赖个别的误差较大的点或甚至可能以及出错的样本的点,而计算出来的决策边界线和隔离带,那准确吗?万一其中的最近的样本点的标签出错了怎么办?这就会导致计算出来的决策边界线和隔离带是基于错误信息得到的,那决策边界和隔离带难准确吗?很显然,答案是否定的。
Hard margin算法最大的优点是依赖少量的样本点,效率高,当样本点非常精确,且边界处没有误差时,这种算法的优势就非常明显。
然后,当边界处的样本点误差较大,甚至有错误时,优点也就变成了缺点,依据局部错误的信息,而不是依据全局的宏观信息得到的决策边界的准确性就大打折扣了。

一句话,Hard margin容错的能力太小了,soft margin就是在Hard margin算法的基础之上,为之增加容错能力进一步的优化算法,而不是完全推翻Hard margin的算法。
4.2 Soft margin的解决之道
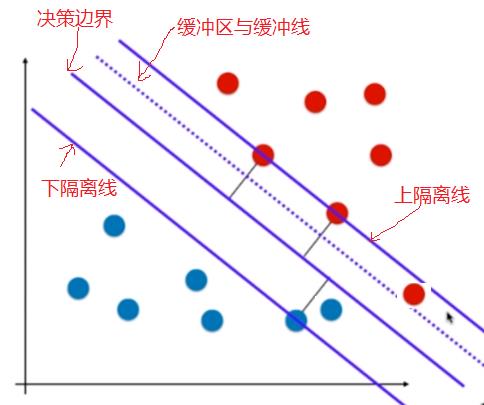
(1)依然保留原先的隔离区
(2)在决策边界和隔离区边界中间增加一个缓冲地带,通过虚线表示,这里称为缓冲线,在缓冲区,允许出现部分的样本的点。
(3)在非缓冲地带隔离区,亦然不允许出现任何样本点。
(4)当缓冲线越接近边界线的时候,容错能力越强,但决策边界需要的信息越多。
如何用数学表达上述的缓冲线呢?
4.3 Soft margin的数学表达式=》把现实问题转换最优化问题

4.4 soft margin的参数求解:最优化求解过程=》梯度下降。


通过上述方法计算得到的W, B参数,具备了一定的容错能力。

可以通过超参数C来控制缓冲带的权重和影响能力。
C越小,缓冲区越小
C越大,缓冲区越大。
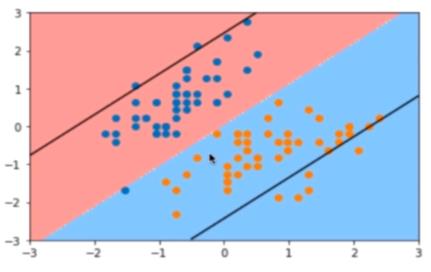
上图允许隔离带中包含一定的样本。
第5章 数据的正则化/规范化
5.1 为什么要正则化Normalization
在机器学习不同,不同维度的特征值,其量纲是不同的,导致不同维度的特征值,其数值范围相差非常大,有些数值空间在【0,1】之间,有些维度的数值范围在几万,甚至几十万之间。
这些不同量纲不同数值范围的数据放到一起Y=F(X1,X2,X3...), 导致大范围的数据,很容易把小数值数据吞并掉,这种吞并是负面的,因为他们的量纲不同,大数值不代表真的影响大。
如1公里与100毫米,并不能说明100毫米,就比1公里大。
不同量纲的不同数值范围,还带来一个严重的问题,就是大数值的一个微小的误差,都会导致小数值数据失效。
这就是大数字吃掉小数字问题。
为了解决上述问题,需要把不同维度的特征数据,全部正则化到【0,1】区间。
Normalization虽然解决了自身的输入数据不同维度的规范化,但他没有解决如何规范的问题。
5.2 什么是正则化Normalization
Normalization的中文翻译一般叫做“规范化”,是一种对数值的特殊函数变换方法,也就是说假设原始的某个数值是x,套上一个起到规范化作用的函数,对规范化之前的数值x进行转换,形成一个规范化后的数值。
规范化,完成了不同维度数据的规范和统一,但并没有对如何规范作出规定。就拿考试来讲,是规范到100制度,还是规范到150制上,并不要求,只要所有的输入都规范到相同的空间就行了。
5.3 如何正则化Normalization
[人工智能-深度学习-43]:输入预处理 - 规范化Normalization、标准化Standardization、正态分布、算术平均、方差_文火冰糖的硅基工坊的博客-CSDN博客
后记:
上述的探讨的是线性可分的数据集,对于线性不可分的数据集,SVM是如何处理的呢?
升维,转换成高纬度的线性可分,还是有其他方法?
参考:
独家首播!Python机器学习+算法+人工智能+项目实战【建议收藏】_哔哩哔哩_bilibili
以上是关于[机器学习与scikit-learn-34]:算法-分类-支持向量机SVM的基本简介与基本原理-线性分类的主要内容,如果未能解决你的问题,请参考以下文章