支持向量机低维与高维

Posted 2021-04-26 花牛乱弹琴

前面说了很多关于向量空间、超平面、分类函数等等概念。

要实现二分类，也就是要把向量空间分成两部分，需要以下二者之一

1. 高维空间被超平面分开

2. 低维空间被高维函数分开

实际上两者是一个意思。看看下面这个例子，2维空间中的向量被一个3维空间中的曲面所分开。

而这个曲面是4维超平面，可以分开5维的空间。

所以， 我们就把2维向量全部映射到5维空间去，再用一个4维超平面切开，就解决了。

再来详细看一下几维超平面的概念。

形状越“复杂”，实际就相当于维数越高，它的分类能力也就越强。

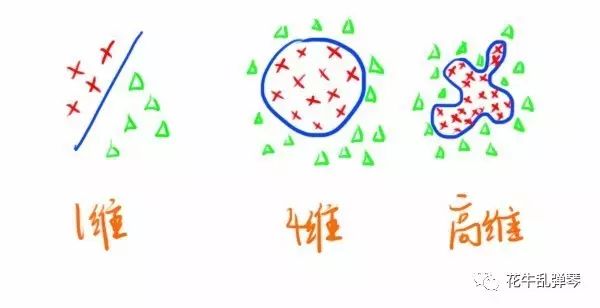
维数很高时，就像下面这个样子：

那么问题就来了，我们需要分类能力强的函数，也就是需要高维函数，但是维数太高就什么都不方便了，比如编程不方便、求解不方便、证明不方便。

万幸，科学家发明了下面这个函数。

你知道是哪位科学家吗？说出来吓死你。他就是--

高斯

是的，就是约翰·卡尔·弗里德里希·高斯（1777-1855）。

我小时候就知道他发明过1+2+3+...+100的快速计算公式，所以对他老人家的伟大，我已经习惯了。

他老人家死的那年， 地球人连电灯泡都没发明，更不要说电脑了，更更更不要说支持向量机了。

高斯到底发明啥了，且待下回分解。