8步学习SVM（支持向量机）（附改进实现SVM算法代码）

Posted 2021-04-26 机器学习算法与自然语言处理

重磅干货，第一时间送达

https://www.zhihu.com/question/31211585/answer/640501555

以下为正文：

学习 SVM 的最好方法是实现一个 SVM，可讲理论的很多，讲实现的太少了。

假设你已经读懂了 SVM 的原理，并了解公式怎么推导出来的，比如到这里：

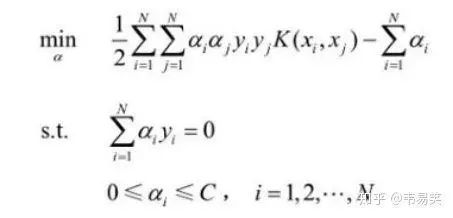
SVM 的问题就变成：求解一系列满足约束的 alpha 值，使得上面那个函数可以取到最小值。然后记录下这些非零的 alpha 值和对应样本中的 x 值和 y 值，就完成学习了，然后预测的时候用：

上面的公式计算出 f(x) ，如果返回值 > 0 那么是 +1 类别，否则是 -1 类别，先把这一步怎么来的，为什么这么来找篇文章读懂，不然你会做的一头雾水。

那么剩下的 SVM 实现问题就是如何求解这个函数的极值。方法有很多，我们先找个起点，比如 Platt 的SMO 算法（https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-98-14.pdf），它后面有伪代码描述怎么快速求解 SVM 的各个系数。

第一步：实现传统的 SMO 算法

现在大部分的 SVM 开源实现，源头都是 platt 的 smo 算法，读完他的文章和推导，然后照着伪代码写就行了，核心代码没几行：

target = desired output vector

point = training point matrix

procedure takeStep(i1,i2)

  if (i1 == i2) return 0

  alph1 = Lagrange multiplier for i1
  y1 = target[i1]
  E1 = SVM output on point[i1] – y1 (check in error cache)
  s = y1*y2
  Compute L, H via equations (13) and (14)
  if (L == H)
    return 0
  k11 = kernel(point[i1],point[i1])
  k12 = kernel(point[i1],point[i2])
  k22 = kernel(point[i2],point[i2])
  eta = k11+k22-2*k12
  if (eta > 0)
  {
    a2 = alph2 + y2*(E1-E2)/eta
    if (a2 < L) a2 = L
    else if (a2 > H) a2 = H
  }
  else
  {
    Lobj = objective function at a2=L
    Hobj = objective function at a2=H
    if (Lobj < Hobj-eps)
      a2 = L
    else if (Lobj > Hobj+eps)
      a2 = H
    else
      a2 = alph2
  }
  if (|a2-alph2| < eps*(a2+alph2+eps))
    return 0
  a1 = alph1+s*(alph2-a2)
  Update threshold to reflect change in Lagrange multipliers
  Update weight vector to reflect change in a1 & a2, if SVM is linear
  Update error cache using new Lagrange multipliers
  Store a1 in the alpha array
  Store a2 in the alpha array
  return 1

endprocedure

核心代码很紧凑，就是给定两个 ai, aj，然后迭代出新的 ai, aj 出来，还有一层循环会不停的选择最需要被优化的系数 ai, aj，然后调用这个函数。如何更新权重和 b 变量（threshold）文章里面都有说，再多调试一下，可以用 python 先调试，再换成 C/C++，保证得到一个正确可用的 SVM 程序，这是后面的基础。

第二步：实现核函数缓存

观察下上面的伪代码，开销最大的就是计算核函数 K(xi, xj)，有些计算又反复用到，一个 100 个样本的数据集求解，假设总共要调用核函数 20 万次，但是 xi, xj 的组和只有 100x100=1 万种，有缓存的话你的效率可以提升 20 倍。

样本太大时，如果你想存储所有核函数的组和，需要 N*N * sizeof(double) 的空间，如果训练集有 10 万个样本，那么需要 76 GB 的内存，显然是不可能实现的，所以核函数缓存是一个有限空间的 LRU 缓存，SVM 的 SMO 求解过程中其实会反复用到特定的几个有限的核函数求解，所以命中率不用担心。

有了这个核函数缓存，你的 SVM 求解程序能瞬间快几十倍。

第三步：优化误差值求解

注意看上面的伪代码，里面需要计算一个估计值和真实值的误差 Ei 和 Ej，他们的求解方法是：

E(i) = f(xi) - yi

这就是目前为止 SMO 这段为代码里代价最高的函数，因为回顾下上面的公式，计算一遍 f(x) 需要 for 循环做乘法加法。

platt 的文章建议是做一个 E 函数的缓存，方便后面选择 i, j 时比较，我看到很多入门版本 SVM 实现都是这么做。其实这是有问题的，后面我们会说到。最好的方式是定义一个 g(x) 令其等于：

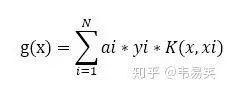
也就是 f(x) 公式除了 b 以外前面的最费时的计算，那么我们随时可以计算误差：

E(j) = g(xj) + b - yj

所以最好的办法是对 g(x) 进行缓存，platt 的方法里因为所有 alpha 值初始化成了 0，所以 g(x) 一开始就可以全部设置成 0，稍微观察一下 g(x) 的公式，你就会发现，因为去掉了 b 的干扰，而每次 SMO 迭代更新 ai, aj 参数时，这两个值都是线性变化的，所以我们可以给 g(x) 求关于 a 的偏导，假设 ai，aj 变化了步长 delta，那么所有样本对应的 g(x) 加上 delta 乘以针对 ai, aj 的偏导数就行了，具体代码类似：

double Kik = kernel(i, k);

double Kjk = kernel(j, k);

G[k] += delta_alpha_i * Kik * y[i] + delta_alpha_j * Kjk * y[j];

把这段代码放在 takeStep 后面，每次成功更新一对 ai, aj 以后，更新所有样本对应的 g(x) 缓存，这样通过每次迭代更新 g(x) 避免了大量的重复计算。

这其实是很直白的一种优化方式，我查了一下，有人专门发论文就讲了个类似的方法。

第四步：实现冷热数据分离

Platt 的文章里也证明过一旦某个 alpha 出于边界（0 或者 C）的时候，就很不容易变动，而且伪代码也是优先在工作集里寻找 > 0 and < C 的 alpha 值进行优化，找不到了，再对工作集整体的 alpha 值进行迭代。

那么我们势必就可以把工作集分成两个部分，热数据在前（大于 0 小于 C 的 alpha 值），冷数据在后（小于等于 0 或者大于等于 C 的 alpha）。

随着迭代加深，会发现大部分时候只需要在热数据里求解，并且热数据的大小会逐步不停的收缩，所以区分了冷热以后 SVM 大部分都在针对有限的热数据迭代，偶尔不行了，再全部迭代一次，然后又回到冷热迭代，性能又能提高不少。

第五步：支持 Ensemble

大家都知道，通过 Ensemble 可以让多个不同的弱模型组和成一个强模型，而传统 SVM 实现并不能适应一些类似 AdaBoost 的集成方法，所以我们需要做一些改动。可以让外面针对某一个分类传入一个“权重”过来，修正 SVM 的识别结果。

最传统的修改方式就是将不等式约束 C 分为 Cp 和 Cn 两个针对 +1 分类的 C 及针对 -1 分类的 C。修改方式是直接用原始的 C 乘以各自分类的权重，得到 Cp 和 Cn，然后迭代时，不同的样本根据它的 y 值符号，用不同的 C 值带入计算。

这样 SVM 就能用各种集成方法同其他模型一起组成更为强大精准的模型了。

实现到这一步你就得到了功能上和性能上同 libsvm 类似的东西，接下来我们继续优化。

第六步：继续优化核函数计算

核函数缓存非常消耗内存，libsvm 数学上已经没得挑了，但是工程方面还有很大改进余地，比如它的核缓存实现。

由于标准 SVM 核函数用的是两个高维矢量的内积，根据内积的几个条件，SVM 的核函数又是一个正定核，即 K(xi, xj) = K(xj, xi)，那么我们同样的内存还能再多存一倍的核函数，性能又能有所提升。

针对核函数的计算和存储有很多优化方式，比如有人对 NxN 的核函数矩阵进行采样，只计算有限的几个核函数，然后通过插值的方式求解出中间的值。还有人用 float 存储核函数值，又降低了一倍空间需求。

第七步：支持稀疏向量和非稀疏向量

对于高维样本，比如文字这些，可能有上千维，每个样本的非零特征可能就那么几个，所以稀疏向量会比较高效，libsvm 也是用的稀疏向量。

但是还有很多时候样本是密集向量，比如一共 200 个特征，大部分样本都有 100个以上的非零特征，用稀疏向量存储的话就非常低效了，openCV 的 SVM 实现就是非稀疏向量。

非稀疏向量直接是用数组保存样本每个特征的值，在工程方面就有很多优化方式了，比如用的最多的求核函数的时候，直接上 SIMD 指令或者 CUDA，就能获得更好的计算性能。

所以最好的方式是同时支持稀疏和非稀疏，兼顾时间和空间效率，对不同的数据选择最适合的方式。

第八步：针对线性核进行优化

传统的 SMO 方法，是 SVM 的通用求解方法，然而针对线性核，就是：

K(xi, xj) = xi . xj

还有很多更高效的求解思路，比如 Pegasos 算法就用了一种类似随机梯度下降的方法，快速求 SVM 的解权重 w，如果你的样本适合线性核，使用一些针对性的非 SMO 算法可以极大的优化 SVM 求解，并且能处理更加庞大的数据集，LIBLINEAR 就是做这件事情的。

同时这类算法也适合 online 训练和并行训练，可以逐步更新增量训练新的样本，还可以用到多核和分布式计算来训练模型，这是 SMO 算法做不到的地方。

但是如果碰到非线性核，权重 w 处于高维核空间里（有可能无限维），你没法梯度下降迭代 w，并且 pegasos 的  pdf 里面也没有提到如何用到非线性核上，LIBLINEAR 也没有办法处理非线性核。

或许哪天出个数学家又找到一种更好的方法，可以用类似 pegasos 的方式求解非线性核，那么 SVM 就能有比较大的进展了。

后话

上面八条，你如果实现前三条，基本就能深入理解 SVM 的原理了，如果实现一大半，就可以得到一个类似 libsvm 的东西，全部实现，你就能得到一个比 libsvm 更好用的 SVM 库了。

上面就是如何实现一个相对成熟的 SVM 模型的思路，以及配套优化方法，再往后还有兴趣，可以接着实现支持向量回归，也是一个很有用的东西。

扫码加入Python算法学习群，备注

“学校、机构+昵称”

未按要求备注不予通过哦

推荐阅读：