松松学算法之排序系列--希尔排序
Posted 站在树上的松鼠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了松松学算法之排序系列--希尔排序相关的知识,希望对你有一定的参考价值。
昨天讲的插入排序,是一种简单插入排序,大伙不知道看没看出啥问题,就是当待插入的数比较小或者比较大的时候,插入的时候,需要腾的位置次数会明显增多,这明显是会降低效率的。那么希尔排序是不是解决这样的问题呢。我们就来看看。
希尔排序也是一种插入排序,希尔排序有点分治的意思,就是一个大问题拆成小问题去解决。我们来看下他的思路。
1 将数组分成几组,每组之间的距离为增量gap,起初的gap一般为数组的一半,即gap=arr.length-1
颜色相同表示同一组,每个数之间相差4 即10/2-1。分组以后在组内再次进行排序,有两种方法,一种交换法,效率低,一种移位法,效率较高,和插入排序类似。推导过程采用交换法。
2 我们逐步推导出,如何进行上述步骤。
//逐步推倒//希尔排序第一轮//第一轮是将10个数分为了10/2=5组,每组两个,增量5,即每两个数之间相差5-1个//遍历每个分组,i的初始值为当前增量for (int i=5;i < arr.length ;i++ ) {//这一层相当于进行了两数大小比较交换//j从i-5地方开始减,可以认为从i的位置向前走5步,切换到同组的前一个数for(int j=i-5;j >=0;j-=5){//采用交换法比较if(arr[j] > arr[j+5]){int temp=arr[j];arr[j]=arr[j+5];arr[j+5]=temp;}}}
3 第二步推导,此时增量gap变为上一次的一半,即gap=5/2 =2,第三步,此时增量gap变为第二次的一半,即gap=2/1。
//希尔排序第二轮//第二轮排序,是将10个数据分为5/2组,每组5个,增量为2,即每两个数之间相差2-1个for(int i=2;i<arr.length;i++){for(int j=i-2;j>=0;j-=2){//采用交换法比较if(arr[j] > arr[j+2]){int temp=arr[j];arr[j]=arr[j+2];arr[j+2]=temp;}}}//希尔排序的第3轮//第3轮排序,是将10个数据分成2/2=1组个,步长1for (int i = 1; i < arr.length; i++) {for (int j = i - 1; j >= 0; j -= 1) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
4 因此我们推导出了,采用交换法,需要三层循环,一层循环来控制分组,一层用于分组的遍历,一层用于分组内的遍历
//希尔排序的第n轮//第n轮排序,是将m个数分为m/2组,每组m/gap个,增量gapint gap=0; //增量int count=0 //用于记录轮数//这层循环控制不同时候的分组for (gap=arr.length;gap>=0 ;gap/=2 ) {//用于控制分组的遍历for (int i=gap;i<arr.length ;i++ ) {//控制分组内的遍历for (int j=i-gap;j>=0 ;j-=gap ) {//我采用了位运算,相比较temp的交换效率会高点if (arr[j] > arr[j + gap]) { // a:arr[j] b: arr[j+gap]// int temp = arr[j+gap];// arr[j+gap]=arr[j];// arr[j]=temp;arr[j] = arr[j] ^ arr[j + gap];arr[j + gap] = arr[j] ^ arr[j + gap];arr[j] = arr[j] ^ arr[j + gap];}}}}
5 我们看下交换法的运行过程
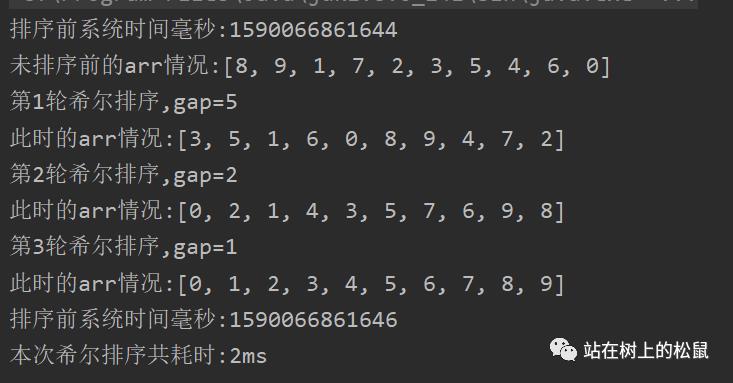
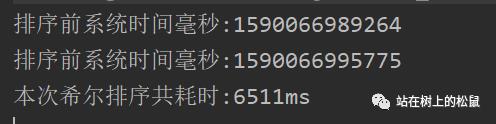
6 我们来试试80000个数,我们可以看到耗费了6秒钟,这是采用位运算的交换的效率
7 我们来看看普通temp的交换的时间
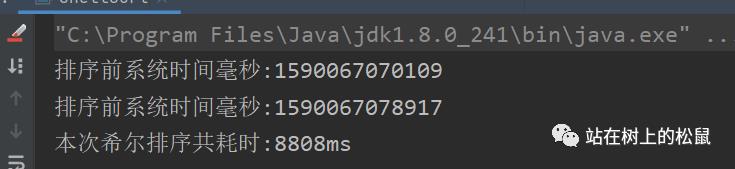
多耗费了2秒。
8 好了。交换法的效率是这样的了,并不快。让我们研究下移位法,再感受一下他的速度。
//移位法也是三层,两层for一层while,//因为移位不确定移位次数,因此采用while更合适,而且就是插入的改进int gap=0; //增量//这一层还是控制分组for (gap=arr.length;gap >=0 ; gap /=2) {//还是控制遍历各个分组for (int i=gap;i <arr.length ;i++ ) {//这个地方就和插入排序很相似//定义一个记录待插入数的变量int insertIndex=i;//记录待插入的数int insertNum=arr[insertIndex];//如果发现同一份组的该数比前一个数小,那么进行移位if(arr[insertIndex] < arr[insertIndex-gap]){//一个分组内,前面元素比后面元素大,则进行移位while (insertIndex-gap>=0&&insertNum < arr[insertIndex-gap]) {//覆盖操作arr[insertIndex]=arr[insertIndex-gap];insertIndex-=gap;}//循环结束,相当于已经腾出位置,将该数放入arr[insertIndex]=insertNum;}}}
9 我们先来验证下它能够正确排序
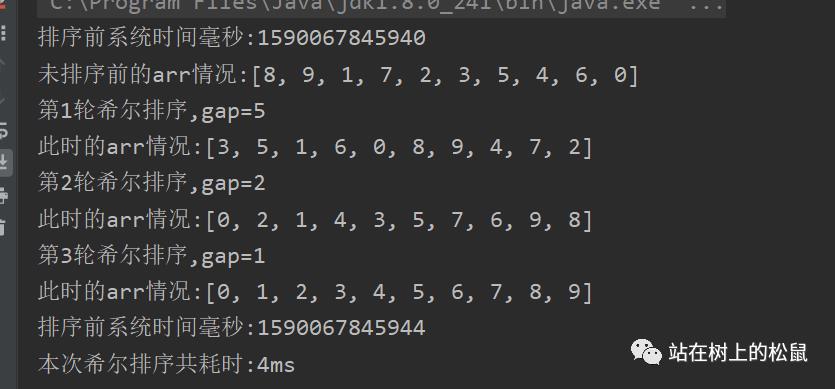
可能这么几个数据量,从时间看,还是位运算的交换法效率高,但是等你去排80000个数,你会感受到他的速度,我们来感受下吧
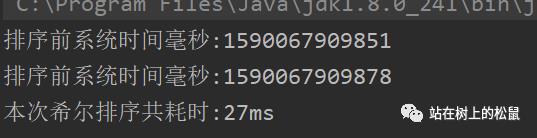
由于数据量庞大因此不进行输出操作,可以看到。。27ms。80000个数用了27ms,那么8000000个呢?
8000000个数用了 2.5秒多,还是效率蛮高的。
好了,今天的希尔排序就写到这了,点个在看哦。觉得不错还可以分享一下。可以留言和我分享感受哦。源码已经放入阅读原文中。
以上是关于松松学算法之排序系列--希尔排序的主要内容,如果未能解决你的问题,请参考以下文章
经典排序算法系列之插入排序和希尔排序----小白理解(python)