排序算法：插入排序

Posted 2021-04-25 程序员囧辉

前言

上一次，我们介绍了排序算法中“龟速三兄弟”的大哥“冒泡排序”。今天，我们继续介绍“龟速三兄弟”中的二哥——“插入排序”。“冒泡排序”的过程和代码相信大多数人都比较熟悉，但是“插入排序”就不见得了。由于同样是“龟速三兄弟”中的一员，但是处理过程没有“冒泡排序”那么简单明了，因此有不少人可能都没接触过“插入排序”，本文将通过例子来介绍“插入排序”的完整过程。

基本思想

将一个数插入一个已经排好序的数据中。

1. 第一次循环时，从第2个数开始处理。我们将第1个数作为已经排好序的数据：当第2个数 > 第1个数时，将第2个数放在第1个数后面一个位置；否则，将第2个数放在第1个数前面。此时，前两个数形成了一个有序的数据。

2. 第二次循环时，我们处理第3个数。此时，前两个数形成了一个有序的数据：首先比较第3个数和第2个数，当第3个数 > 第2个数时，将第3个数放在第2个数后面一个位置并结束此次循环；否则，再和第1个数比较。如果第3个数 > 第1个数，则将第3个数插入第1个数和第2个数中间；否则，第3个数 < 第1个数，则将第3个数放在第1个数前面。此时，前三个数形成了一个有序的数据。

3. 后续的数据同理处理，直至结束。

例子

下面通过一个例子来看看插入排序是怎么工作的。原数组如下。

0	1	2	3	4
19	15	37	12	25

第一次循环：

1.从第2个数开始处理，即array[1]。比较array[1]和arary[0]，即15和19。因为15 < 19，所以将arary[1]放在array[0]的前面，放完后的数组如下。

0	1	2	3	4
15	19	37	12	25

由于是从第2个数开始处理，一直处理到最后一个数。因此，最外层的循环可以写成如下：

for (int i = 1; i < array.length; i++)

至此，第一次循环结束。

第二次循环：

1.处理第3个数，即array[2]。首先比较array[2]和array[1]，即37和19。因为37 > 19，并且前面2个数经过第一次循环后是有序的。因此，直接将37放在array[1]后面的1个位置即array[2]原位置，放完后的数组如下。 

0	1	2	3	4
15	19	37	12	25

至此，第二次循环结束。

第三次循环：

1.处理第4个数，即array[3]。首先比较array[3]和array[2]，即12和37。因为12 < 37，所以37此时在前4个数中可以确定是最大的。因此此时array[3]是37的正确位置，但是array[3]此时被12占着，所以我们需要用一个临时变量temp存储arary[3]的值，然后将37填入array[3]，填完后的数组如下。

结合比较语句，此时的代码可以写成如下，在当前循环 i = 3。

if (array[i] < array[i - 1]) {
    // 临时变量存储array[i]的值
    int temp = array[i];  
    // array[i - 1]填入此时属于它的位置
    array[i] = array[i - 1];  
}

填充完array[3]后，我们需要将下标向前移动一个位置，好将temp（原来的array[3]）跟array[1]进行比较，但是此时下标 i 代表着循环的位置不能移动。因此，我们需要再定义一个变量 j 来记录比较的位置，因此将上述代码优化成如下：

// 当array[i]比arra[i - 1]小时才进入处理
if (array[i] < array[i - 1]) {
    // 临时变量存储array[i]的值
    int temp = array[i];  
    // 定义变量j记录比较的位置
    int j = i;  
    // 将比temp大的数往后挪一个位置，为temp腾出一个合适位置
    while (j > 0 && temp < array[j - 1]) {  
        array[j] = array[j - 1];  
        j--;    // 填充完后, 继续向前比较 
    }  
}

2.此时 j 移动到下标2，比较temp和array[1]，即12和19。因为12 < 19，并且原来array[2]位置的数37此时已经填入array[3]，因此此时array[2]相当于一个坑，直接将19填入即可。将19填入array[2]时，array[1]又形成了一个新的坑，此时的数组如下。

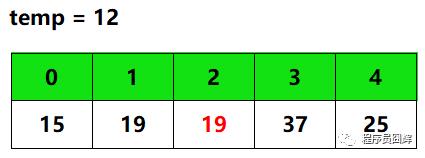
填完后，将下标 j 继续向前移动一个位置。

3.此时 j 移动到下标1，此时比较temp和array[0]，即12和15。因为12 < 15，并且原来array[1]位置的数19此时已经填入array[2]，因此直接将15填入array[1]，此时array[0]又形成了一个新的坑，此时的数组如下。

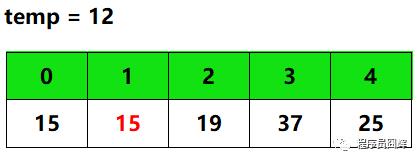
4.此时 j 移动到下标0，已经没有前面的数可以比较了。因此，array[0]即为temp的位置，将temp填入array[0]后结束此次循环，此时的数组如下。

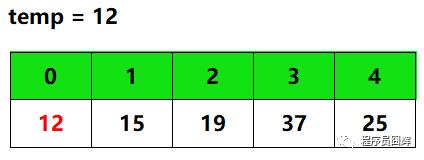
结合上面的代码，将temp填入对应位置的代码也加上后，代码如下：

// 当array[i]比arra[i - 1]小时才进入处理
if (array[i] < array[i - 1]) {
    // 临时变量存储array[i]的值
    int temp = array[i];  
    // 从当前位置开始处理
    int j = i;  
    // 将比temp大的数往后挪一个位置，为temp腾出一个合适位置
    while (j > 0 && temp < array[j - 1]) {  
        array[j] = array[j - 1];  
        j--;    // 填充完后, 继续向前比较 
    }  
    // 将temp放在属于它的位置上
    array[j] = temp;  
}  

第四次循环

1.处理第5个数，即array[4]。首先比较array[4]和array[3]，即25和37。因为25 < 37，所以将25赋值给temp，并将37填入array[4]的位置，并将下标 j 向前移动一个位置，此时的数组如下。

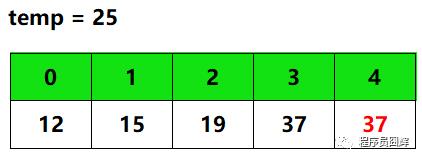
2.此时 j 移动到下标3，此时比较temp和array[2]，即25和19。因为25 > 19，所以array[3]即为25的位置，将25填入array[3]后结束此次循环。

0	1	2	3	4
12	15	19	25	37

至此，整个排序过程结束。

完整过程

最后我们通过以下动图来看插入排序的整个过程，图中红色的柱子为当前要插入的数，橘黄色的柱子为当前已经排好序的数据，绿色的柱子为正在跟红色的柱子比较的数，浅蓝色的柱子为还未插入的数。

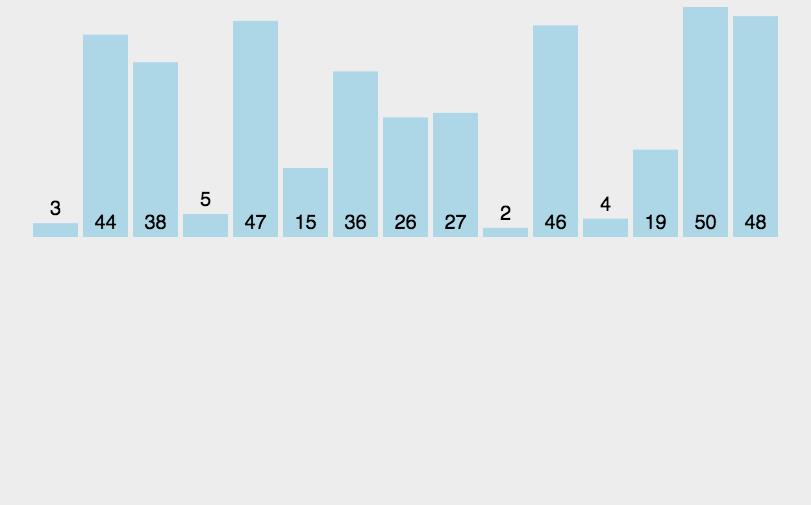
整合

上文的例子中已经基本将逻辑代码都写清了，我们将外层循环和里面的处理逻辑代码结合到一起，代码如下。

时间复杂度

在最坏的情况下，即整个数组是倒序的，比较次数 = 1 + 2 + 3 + ... + (n - 2) + (n - 1) = n * (n - 1) / 2，此时的时间复杂度为：O(n^2)。

在最好的情况下，即整个数组是正序的，比较次数 = n - 1，此时的时间复杂度为：O(n)。

使用场景

插入排序和冒泡排序一样。在进行量比较大的排序时，最好不要使用。在1000个数字以内的排序，用插入排序是可以接受的。1000个随机数使用插入排序耗时一般在5毫秒以内，但是当数字个数达到10000个时，耗时会达到30+毫秒，有比较明显的耗时，需要慎重使用。

相关阅读

—————END—————