使用WebGL验证简单的图像变换理论

Posted 2021-04-25 陛格DOG

述说几何对象的变换

计算机科学家希望把看到的物体按照某种公理描述出来，视同一律把物体的元素看成抽象的数据类型，简称ADT，然后，我们可以对任何物体不带任何偏见的用ADT数据来描述（包括你），几何ADT 包括标量、点、向量，可以实现几何运算规则，其中的运算过程我们称之为仿射变换.

变换是需要参照的

一个三维空间中，很容易想到X,Y,Z三个轴，坐标系是关于这三个轴（三个线性无关的向量）的基向量确定了坐标系，用这三个基向量和基向量上的标量产生的向量来表示元素的构成。原点和基向量决定了一个标架，用一个不严谨的例子来描述是：一个人站在地球的p点处，然后描述成，关于在p点的基础上，根据地球地心为上的，X,Y,Z方向的基向量的分量描述的向量（这是我自己的想法，不喜可喷。。），用数学公式表示是

怎么描述用户看到了另一个位置上的一个物体

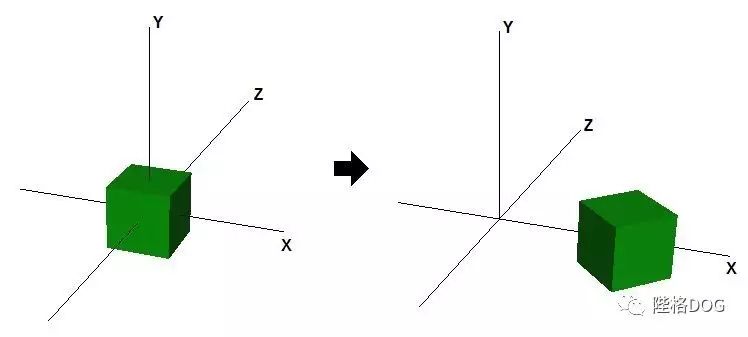
在一个坐标系中，我们对模型在坐标系上的用标架来定义几何对象，模型的标架被称为对象标架，然后这些对象标架又放到世界标架中，当然，用户观察的时候是需要位置和方向的，这时候需要一个照相机标架，一个3d元素表示出来的时候，是通过从对象标架到照相机标架的转换，由为模-视变换矩阵来完成。我以前开发D3D程序的时候，定义为世界矩阵和视图矩阵

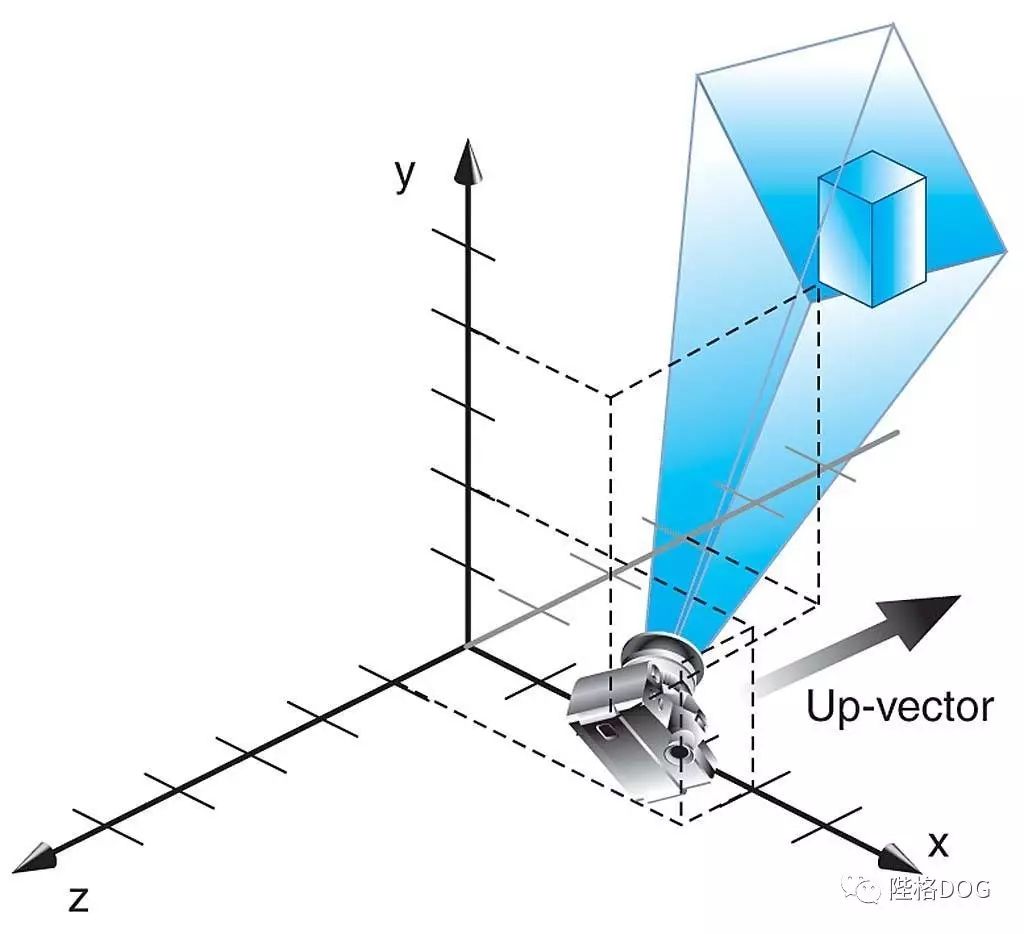
齐次坐标

任何两个标架可以通过不同基下的表示进行变换，记两个基为 T,M ，则T用M的表示为

看公式很好理解吧，就是一个线性变换的应用，求矩阵的逆

但是由于通过基的三个向量来表示一个标架（x,y,z,P），我们还缺一个原点P，因此通过矩阵描述的时候，需要把p点给带上,那么我们可以用矩阵的乘法来把点Pn形式的表示为

现在对于（a,b,c,P) 和 (l,m,n,Q) 的两个标架，可以写成方程

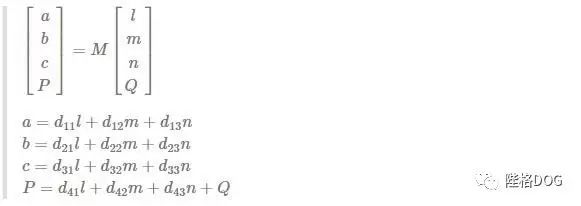
则 得出来的4x4矩阵为

假设对于 j 和 k 是同一个向量分别在两个标架下的齐次坐标表示

用程序来实现

上吧 WebGL:不过我不打算说开发基础哦 ^_^

1、我们通过网格来创建一个正方体，其顶点和网格索引分别表示为:

    //顶点:
    var vertices = [
        vec3( -0.5, -0.5,  0.5 ),
        vec3( -0.5,  0.5,  0.5 ),
        vec3(  0.5,  0.5,  0.5 ),
        vec3(  0.5, -0.5,  0.5 ),
        vec3( -0.5, -0.5, -0.5 ),
        vec3( -0.5,  0.5, -0.5 ),
        vec3(  0.5,  0.5, -0.5 ),
        vec3(  0.5, -0.5, -0.5 )
    ];

    //网格索引
    var indices = [
        1, 0, 3,
        3, 2, 1,
        2, 3, 7,
        7, 6, 2,
        3, 0, 4,
        4, 7, 3,
        6, 5, 1,
        1, 2, 6,
        4, 5, 6,
        6, 7, 4,
        5, 4, 0,
        0, 1, 5
    ];

2、 上色

五颜六色相互交错,不错＾＿＾

var vertexColors=[
        [ 0.0, 0.0, 0.0, 1.0 ],  
        [ 1.0, 0.0, 0.0, 1.0 ],  
        [ 1.0, 1.0, 0.0, 1.0 ],   
        [ 0.0, 1.0, 0.0, 1.0 ],  
        [ 0.0, 0.0, 1.0, 1.0 ],   
        [ 1.0, 0.0, 1.0, 1.0 ],  
        [ 0.0, 1.0, 1.0, 1.0 ],  
        [ 1.0, 1.0, 1.0, 1.0 ]   
    ];

旋转吧

通过公式描述旋转

利用两角的正弦和余弦公式可以得到:

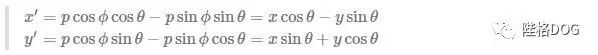
矩阵表示法：

齐次坐标的矩阵表示

使用创建绕X轴旋转的方法

使用rotate变换函数可以得到变换矩阵，注意，下面使用了左乘变换矩阵，可以想想有没有毛病 ^_^

function rotateX(m,angle) {
    return  mult(m, rotate(angle, [1,0,0]));}

创建绕Y轴旋转的方法

function rotateY(m,angle) {
    return  mult(m, rotate(angle, [0,1,0]));}

创建绕Z轴旋转的方法

function rotateY(m,angle) {
    return  mult(m, rotate(angle, [0,0,1]));}

使用uniform矩阵来实现模-视变换矩阵

定义着色器

<script id="vertex-shader" type="x-shader/x-vertex">precision mediump float;

attribute vec4 vPosition;
attribute vec4 vColor;
varying vec4 fColor;
uniform mat4 modelViewMatrix;

void main()
{   

    fColor = vColor;
    gl_Position = modelViewMatrix * vPosition;

}</script>

设置模-视矩阵和渲染

function init(){...var modelViewMatrixLoc;var rotationMatrix;modelViewMatrixLoc = gl.getUniformLocation(program,"modelViewMatrix");rotationMatrix = mat4();gl.uniformMatrix4fv(modelViewMatrixLoc, false, flatten(rotationMatrix));...render();}function render(){
    setTimeout(function (){
    gl.clear(gl.COLOR_BUFFER_BIT|gl.DEPTH_BUFFER_BIT);
    //通过用户输入获取旋转系数
    xAngle =  document.getElementById("x").value;
    yAngle =  document.getElementById("y").value;
    zAngle =  document.getElementById("z").value;
    //绕X轴旋转
    rotationMatrix = rotateX(rotationMatrix, xAngle);
    //绕y轴旋转
    rotationMatrix = rotateY(rotationMatrix, yAngle);
    //绕z轴旋转
    rotationMatrix = rotateY(rotationMatrix, zAngle);
    gl.uniformMatrix4fv(modelViewMatrixLoc, false, flatten(rotationMatrix));
    gl.drawElements(gl.TRIANGLES,36,gl.UNSIGNED_BYTE,0);
    requestAnimFrame(render);
    },100);}

使用uniform矩阵+ rotate来实现模-视变换矩阵来实现太简单了以至于体现不了数学公式是吧？

使用只向GPU发送旋转角度，模-视变换矩阵由顶掉着色器来计算

attribute vec4 vPosition;
attribute vec4 vColor;
varying vec4 fColor;
uniform vec3 theta;

void main(){
    vec3 angles = radians(theta);
    vec3 c = cos(angles);
    vec3 s = sin(angles);

    mat4 rx = mat4( 1.0,0.0,0.0,0.0,
                    0.0,c.x,s.x,0.0,
                    1.0,-s.x,c.x,0.0,
                    0.0,0.0,0.0,1.0,
                );

    mat4 ry = mat4( c.y,-s.z,0.0,0.0,
                    0.0,1.0,0.0,0.0,
                    s.y,0.0,c.y,0.0,
                    0.0,0.0,0.0,1.0,
                );

    mat4 rz = mat4( c.z,-s.z,0.0,0.0,
                    s.z,c.z,0.0,0.0,
                    0.0,0.0,1.0,0.0,
                    0.0,0.0,0.0,1.0,
                );
    fColor = vColor;
    gl_Position = rz * ry * rz * vPosition;
}

渲染函数:

var theta = [0.0,0.0,0.0];var xAxis = 0;var yAxis = 1;var thetaLoc ;thetaLoc = gl.getUniformLocation(program,"theta");function render(){
    setTimeout(function (){
    gl.clear(gl.COLOR_BUFFER_BIT|gl.DEPTH_BUFFER_BIT);
    //通过用户输入获取旋转系数
    xAngle =  document.getElementById("x").value;
    yAngle =  document.getElementById("y").value;
    zAngle =  document.getElementById("z").value;
    //绕X轴旋转
    theta[xAxis] +=xAngle;
    //绕Y轴旋转
    theta[yAxis] +=yAngle;
    gl.uniform3fv(thetaLoc, false, flatten(theta));
    gl.drawElements(gl.TRIANGLES,36,gl.UNSIGNED_BYTE,0);
    requestAnimFrame(render);
    },100);}

展示如下图：