shader编程-二维空间中使用矩阵实现物体的旋转缩放平移变换（WebGL-Shader开发基础03）
Posted 点燃火柴
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了shader编程-二维空间中使用矩阵实现物体的旋转缩放平移变换（WebGL-Shader开发基础03）相关的知识，希望对你有一定的参考价值。
shader编程-二维空间中使用矩阵实现物体的旋转、缩放、平移变换
1. 变换前物体的绘制
在进行变换操前先绘制出要操作的物体，我们就简单的绘制一个矩形来代表，利用之前的绘制矩形的代码稍作修改，之前用的是step函数，现在调整为smoothstep函数，因为旋转时使用step函数绘制的矩形边缘会出现锯齿，具体如下
float box(vec3 st){
float right = 0.15;
float top = 0.1;
float blur = 0.002;//边缘模糊系数
//通过右上角绘制原点对称的四边形
vec2 bl = 1.0-smoothstep(vec2(right,top)-blur,vec2(right,top)+blur,abs(st.xy));
float pct = bl.x * bl.y;
return pct;
}
绘制的结果如下，一个小矩形出现在绘制区域中央
2. 物体旋转的实现
我们使用矩阵来实现物体的旋转，先来看看齐次坐标下的旋转矩阵长什么样
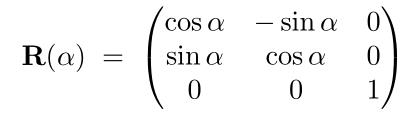
上面的矩阵用于二维平面下对物体进行旋转变换，旋转矩阵的相关知识，请参照这篇文章图形学中的基本变换
接下来看看获取旋转矩阵函数的代码
mat3 rotate2d(float _angle){
float angle = radians(_angle);//角度转为弧度
return mat3(cos(angle),-sin(angle),0.0,
sin(angle),cos(angle),0.0,
0.0,0.0,1.0
);
}
调用的时候需要注意一下，齐次坐标下返回的旋转矩阵是一个三维矩阵，所以先将屏幕坐标转为三维坐标，以匹配旋转矩阵，与旋转矩阵相乘后相当于将整个屏幕坐标旋转了，接着绘图，绘出的图就带旋转效果了，具体参照如下代码
void main( void ) {
//窗口坐标调整为[-1,1],坐标原点在屏幕中心
vec2 _st = (gl_FragCoord.xy * 2. - u_resolution) / u_resolution.y;
vec3 line_color = vec3(1.0,1.0,0.0);
vec3 color = vec3(0.6);//背景色
float pct = 0.0;
//将屏幕坐标转为三维坐标，使之在和矩阵相乘时相匹配
vec3 st = vec3(_st,1.0);
//使用旋转矩阵使矩形顺时针旋转10度
st *= rotate2d(10.0);
pct = box(st);
color = mix(color,line_color,pct);
gl_FragColor = vec4(color, 1);
}
看看运行结果，矩形在原来的基础上顺时针旋转了10度
如果想逆时针旋转10度，只需要在参数前添加个负号
st *= rotate2d(-10.0);
如果你想让它不停旋转，需要用到u_time变量，之所以乘以30.0，是为了让物体旋转的更快一些
st *= rotate2d(u_time*30.0);
3. 物体缩放的实现
同样先来看看齐次坐标下缩放矩阵的模样
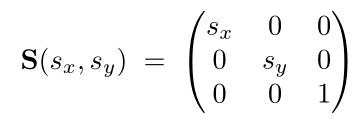
该矩阵相关知识还是参照这篇文章图形学中的基本变换
接着我们编写返回缩放矩阵的函数，如下
mat3 scale2d(vec2 scale){
//缩放矩阵作用于坐标系，所以放大和缩小刚好相反，为了使用习惯，缩放参数取倒数
return mat3(1.0/scale.x,0.0,0.0,
0.0,1.0/scale.y,0.0,
0.0,0.0,1.0
);
}
绘制物体前，将屏幕坐标与该矩阵相乘
st *= scale2d(vec2(2.0,4.0));
执行上面的代码物体x轴方向放大2倍，y轴方向放大4倍，结果如下
4. 物体平移的实现
下图是齐次坐标下平移矩阵
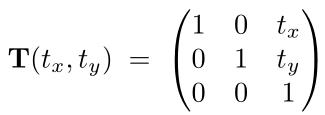
该矩阵相关知识还是参照这篇文章图形学中的基本变换
开始编写返回平移矩阵的函数，如下
mat3 translation2d(vec2 translate){
//平移矩阵作用于坐标系，所以平移的方向相反，为了使用习惯，缩放参数取负
return mat3(1.0,0.0,-translate.x,
0.0,1.0,-translate.y,
0.0,0.0,1.0
);
}
绘图前屏幕坐标与平移坐标相乘
st *= translation2d(vec2(0.2,0.4));
执行结果如下图，与原物体相比，在x轴方向平移0.2，y轴方向平移0.4
如果将代码调整成下面的代码，则物体沿着y轴像弹簧一样做上下往复运动
st *= translation2d(vec2(0.0,sin(u_time)*0.5));
如果替换为下面代码，则物体会沿着半径为0.5的圆环上做环形运动
st *= translation2d(vec2(cos(u_time)*0.5,sin(u_time)*0.5));
至此，如果你已经掌握物体的基本变换就，其实各种变换是可以叠加的，只需要不断地乘上变换矩阵，例如让物体既自己旋转，又通过平移矩阵实现环形运动，可使用以下代码
st *= rotate2d(u_time*30.0);
st *= translation2d(vec2(cos(u_time)*0.5,sin(u_time)*0.5));
5. 平移与缩放另外一种实现方式
平移与缩放可以通过另外一种不使用矩阵的方式实现，原理就是改变屏幕坐标，物体则以相反的变换变化，例如将屏幕坐标乘以2，相当于屏幕坐标放大两倍，而绘制物体时大小不变，则物体看起来像缩小为原来的一半，如果你对屏幕坐标的x轴减0.5个单位，绘制的结果是物体向右移动0.5个单位
一些简单的平移与缩放示例代码
//非矩阵的放大缩小方式
//st *=3.0;//屏幕坐标放大3倍，相当于物体缩小3倍
//st /=3.0;//屏幕坐标缩小3倍，相当于物体放大3倍
//非矩阵的平移方式
//st.x -=0.2;//物体向右移0.2个单位
//st -=0.4;//物体向右向上移0.4个单位
//st.x +=0.3;//物体向左移0.3个单位
6. 所有示例代码
<body>
<div id="container"></div>
<script src="http://www.yanhuangxueyuan.com/versions/threejsR92/build/three.js"></script>
<script>
var container;
var camera, scene, renderer;
var uniforms;
var vertexShader = `
void main() {
gl_Position = vec4( position, 1.0 );
}
`
var fragmentShader = `
#ifdef GL_ES
precision mediump float;
#define sat(x) clamp(x, 0.0, 1.0)
#endif
uniform float u_time;
uniform vec2 u_mouse;
uniform vec2 u_resolution;
mat3 rotate2d(float _angle){
float angle = radians(_angle);//角度转为弧度
return mat3(cos(angle),-sin(angle),0.0,
sin(angle),cos(angle),0.0,
0.0,0.0,1.0
);
}
mat3 scale2d(vec2 scale){
//缩放矩阵作用于坐标系，所以放大和缩小刚好相反，为了使用习惯，缩放参数取倒数
return mat3(1.0/scale.x,0.0,0.0,
0.0,1.0/scale.y,0.0,
0.0,0.0,1.0
);
}
mat3 translation2d(vec2 translate){
//平移矩阵作用于坐标系，所以平移的方向相反，为了使用习惯，缩放参数取负
return mat3(1.0,0.0,-translate.x,
0.0,1.0,-translate.y,
0.0,0.0,1.0
);
}
float box(vec3 st){
float right = 0.15;
float top = 0.1;
float blur = 0.002;//边缘模糊系数
//通过右上角绘制原点对称的四边形
vec2 bl = 1.0-smoothstep(vec2(right,top)-blur,vec2(right,top)+blur,abs(st.xy));
float pct = bl.x * bl.y;
return pct;
}
void main( void ) {
//窗口坐标调整为[-1,1],坐标原点在屏幕中心
vec2 _st = (gl_FragCoord.xy * 2. - u_resolution) / u_resolution.y;
//窗口坐标调整为[0,1],坐标原点在屏幕左下角
//vec2 st = gl_FragCoord.xy/u_resolution;
vec3 line_color = vec3(1.0,1.0,0.0);
vec3 color = vec3(0.6);//背景色
float pct = 0.0;
//将屏幕坐标转为三维坐标，使之在和矩阵相乘时相匹配
vec3 st = vec3(_st,1.0);
//使用旋转矩阵使矩形顺时针旋转10度
//st *= rotate2d(10.0);
//st *= rotate2d(u_time*30.0);
//缩放
//st *= scale2d(vec2(2.0,4.0));
//平移
//st *= translation2d(vec2(0.2,0.4));
//st *= translation2d(vec2(0.0,sin(u_time)*0.5));
//st *= translation2d(vec2(cos(u_time)*0.5,sin(u_time)*0.5));
//非矩阵的放大缩小方式
//st *=3.0;//屏幕坐标放大3倍，相当于物体缩小3倍
//st /=3.0;//屏幕坐标缩小3倍，相当于物体放大3倍
//非矩阵的平移方式
//st.x -=0.2;//物体向右移0.2个单位
//st -=0.4;//物体向右向上移0.4个单位
//st.x +=0.3;//物体向左移0.3个单位
pct = box(st);
color = mix(color,line_color,pct);
gl_FragColor = vec4(color, 1);
}
`
init();
animate();
function init() {
container = document.getElementById('container');
camera = new THREE.Camera();
camera.position.z = 1;
scene = new THREE.Scene();
var geometry = new THREE.PlaneBufferGeometry(2, 2);
uniforms = {
u_time: {
type: "f",
value: 1.0
},
u_resolution: {
type: "v2",
value: new THREE.Vector2()
},
u_mouse: {
type: "v2",
value: new THREE.Vector2()
}
};
var material = new THREE.ShaderMaterial({
uniforms: uniforms,
vertexShader: vertexShader,
fragmentShader: fragmentShader
});
var mesh = new THREE.Mesh(geometry, material);
scene.add(mesh);
renderer = new THREE.WebGLRenderer();
//renderer.setPixelRatio(window.devicePixelRatio);
container.appendChild(renderer.domElement);
onWindowResize();
window.addEventListener('resize', onWindowResize, false);
document.onmousemove = function (e) {
uniforms.u_mouse.value.x = e.pageX
uniforms.u_mouse.value.y = e.pageY
}
}
function onWindowResize(event) {
renderer.setSize(800, 800);
uniforms.u_resolution.value.x = renderer.domElement.width;
uniforms.u_resolution.value.y = renderer.domElement.height;
}
function animate() {
requestAnimationFrame(animate);
render();
}
function render() {
uniforms.u_time.value += 0.02;
renderer.render(scene, camera);
}
</script>
</body>
以上是关于shader编程-二维空间中使用矩阵实现物体的旋转缩放平移变换（WebGL-Shader开发基础03）的主要内容，如果未能解决你的问题，请参考以下文章
shader编程-RayMarching三维场景下模型基本变换旋转缩放平移（WebGL-Shader开发基础09）
shader编程-RayMarching三维场景下模型基本变换旋转缩放平移（WebGL-Shader开发基础09）