Haskell入门篇三：递归

Posted 2021-04-25 Lambda小粽子

在之前阶乘定义中我们提到了递归函数，而阶乘的定义就是用递归函数来实现的。简单来讲，递归函数就是用自己来定义自己，今天我来带大家进一步走近递归函数，并用Haskell函数作为例子来讲讲我我认识的递归。 

在数学和计算机科学中，递归函数的定义有两个要素：

1 一个简单的base case，base case是函数的终止步骤，就比如上面阶乘函数定义中的第一行 factorial 0 = 1就是这个函数的base case。

2 一些特定的规则使得所有其他的情况都会朝向base case发展。这句话有一点绕，简单来讲就是让其他的情况最后都能归结到base case上。就比如我们上面提到的阶乘函数中的第二行定义。

我们来用一个展开作为例子。 

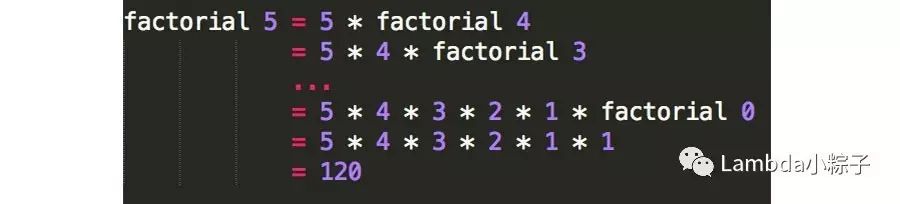
通过这个例子我们可以清楚地看到阶乘函数式如何进行递归的。 

当然也如我们之前提到的，这个函数并没有对所有定义域的值都进行映射，简单来说就是当输入小于零的时候由于这个函数并不能reach到base case而会无限的展开下去不能停止。所以在我们定义递归函数的时候一定要注意将所有的情况都考虑到，保证函数能够对所有的定义域的值进行映射。这个函数的修改我会在之后提到。

相信之前有过编程基础的同学都对递归有所接触，今天我想给大家介绍另一种递归: induction-recursion。这种递归的特点是，在我们定义函数之前，我们需要有一个induction type的变量，同时我们的递归函数会定义在这个induction type的变量上。

什么是induction type呢，我们举一个简单的例子: Nature number。在Haskell中，我们可以这么定义一个变量。一个Nat类型的变量可以为0，或者另一个Nat值的successor。

比如如果我们想要表达5，那么5会被展开为 Succ (Succ (Succ (Succ (Succ Zero))))这个样子。这种类型就是induction type。我们可以类比一下递归类型和递归函数，发现它们出奇的相似。这也是induction-recursion的核心idea，在递归类型的变量上进行递归。

这种递归方法的好处是显而易见的，由于递归类型的递归是可见的(predictable)，所以递归函数的结果是definite的，也就是说这种递归函数会很大程度的避免出现上文提到的由于无法回归base case而使得函数无限展开的情况。当然这种函数因为其递归的要求更为严格，使得我们在定义函数的时候需要投入更多的思考。一些函数式编程语言，如coq和Agda，的递归定义就是这种induction-recursion。我们也会在后面着重提到并介绍着两种语言。这种递归在定义某些函数，如归并排序时会非常的麻烦。

这里我给大家写一个例子方便大家的直观认知。 

这个函数是将nat转化成int。这个函数就是严格按照induction-recursion的方式定义的。当我们接受的变量为Zero时，这也是我们函数和induction type的base case，我们输出0。否则我们调用递归其本身。

相信大家通过我的讲解对递归函数有了更进一步的认知。我所介绍的induction-recursion的递归我会在后面介绍Agda/Coq的时候在着重提到。下一篇文章我会给大家介绍另一种非常重要的同时也是induction type的data type -- List。

---

注：本文为原创内容，转载请标明出处。