实例讲解朴素贝叶斯分类器

Posted 2021-04-25 深度学习自然语言处理

阅读大概需要4分钟

作者 每天进步一点点2015

编辑 zenRRan 有修改

https://ask.hellobi.com/blog/lsxxx2011/6381

若有侵权，马上删除

导读

    

朴素贝叶斯算法仍然是流行的十大挖掘算法之一，该算法是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。接下来我们就详细介绍该算法的知识点及实际应用。

朴素贝叶斯的思想

思想很简单，就是根据某些个先验概率计算Y变量属于某个类别的后验概率，请看下图细细道来：

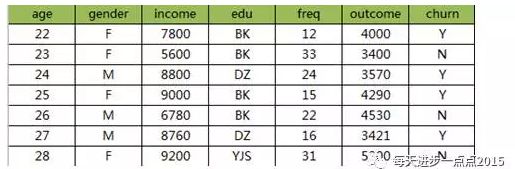
假如，上表中的信息反映的是某P2P企业判断其客户是否会流失(churn)，而影响到该变量的因素包含年龄、性别、收入、教育水平、消费频次、支持。那根据这样一个信息，我该如何理解朴素贝叶斯的思想呢？再来看一下朴素贝叶斯公式：

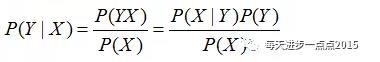
从公式中可知，如果要计算X条件下Y发生的概率，只需要计算出后面等式的三个部分，X事件的概率（P(X)），是X的先验概率、Y属于某类的概率（P(Y)），是Y的先验概率、以及已知Y的某个分类下，事件X的概率（P(X|Y)），是后验概率。从上表中，是可以计算这三种概率值的。即：

P(x)指在所有客户集中，某位22岁的本科女性客户，其月收入为7800元，在12次消费中合计支出4000元的概率；

P(Y)指流失与不流失在所有客户集中的比例；

P(X|Y)指在已知流失的情况下，一位22岁的本科女性客户，其月收入为7800元，在12次消费中合计支出4000元的概率。

如果要确定某个样本归属于哪一类，则需要计算出归属不同类的概率，再从中挑选出最大的概率。

我们把上面的贝叶斯公式写出这样，也许你能更好的理解：

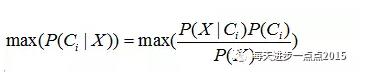
而这个公式告诉我们，需要计算最大的后验概率，只需要计算出分子的最大值即可，而不同水平的概率P(C)非常容易获得，故难点就在于P(X|C)的概率计算。而问题的解决，正是聪明之处，即贝叶斯假设变量X间是条件独立的，故而P(X|C)的概率就可以计算为：

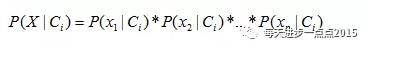
也许，这个公式你不明白，我们举个例子（上表的数据）说明就很容易懂了。

对于离散情况：

假设已知某个客户流失的情况下，其性别为女，教育水平为本科的概率：

上式结果中的分母4为数据集中流失有4条观测，分子2分别是流失的前提下，女性2名，本科2名。

假设已知某个客户未流失的情况下，其性别为女，教育水平为本科的概率

上式结果中的分母3为数据集中未流失的观测数，分子2分别是未流失的前提下，女性2名，本科2名。

从而P(C|X)公式中的分子结果为：

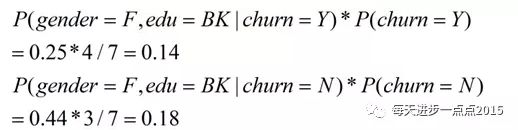
对于连续变量的情况就稍微复杂一点，并非计算频率这么简单，而是假设该连续变量服从正态分布（即使很多数据并不满足这个条件），先来看一下正态分布的密度函数：

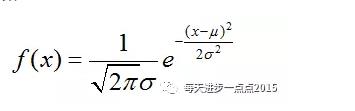
要计算连续变量中某个数值的概率，只需要已知该变量的均值和标准差，再将该数值带入到上面的公式即可。

如果想看实现，R语言代码实践代码链接为：

https://ask.hellobi.com/blog/lsxxx2011/6381

每日托福单词

compound  v.  加剧，恶化  v. 混合

prominent  adj.显著地  adj. 杰出的，著名的

plausible  adj. 看起来合理的，可信的  adj. 似是而非的

juvenile  adj. 青少年的  adj. 幼稚的

handedness  n. 用手习惯，旋向性

推荐阅读：

---

点个赞呗