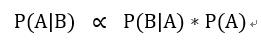本篇文章是我一个大三学妹江颖的学习笔记,我觉得写得通俗易懂,又不失算法严谨性!这里整理一下记录下来。希望对大家有帮助~
这篇文章通俗的讲解了朴素贝叶斯算法,通过回忆,我们知道算法公式如下:
下面我们看一个问题去理解贝叶斯公式及其变形:
现在我们看到用户输入了一个不在字典里的单词,如thew,我们如何去知道用户实际想输入的单词是什么?
我们可以将这个问题抽象成求:


我们现在不妨假设空间有the 和 thaw (为了简化问题,我们的假设空间目前只有the 和 thaw)
实际问题中用的输入法拼写改正器一般只提取编辑距离为2以内的所有已知单词作为假设空间的假设,这样避免放入所有单词。
但是就算是这样的假设,满足的数据量依旧很大,可能有the , they , thaw 等等,所以本文这个问题的假设空间只放入两个元素去讨论(只是为了走完例子,帮助理解,其它原理相同)。
我们现在应用贝叶斯公式,有:

而我们知道,实际上P(他实际输入的单词)是一个定值,因为是已经发生的事实,概率已知,那么我们就可以采用贝叶斯公式的变形:
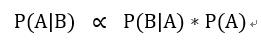
这里写成:

根据假设空间{ the ,thaw },这里有:
我们就比较P(thaw|thew)与p(the|thew)的概率谁大谁小即可!
通过上面分析,我们需要比较P(thaw|thew)与p(the|thew)的概率大小。
也就是需要分别求出p(thew|thaw)*p(thaw)/p(thew)与p(thew|the)*p(the)/p(thew),由于p(thew)是定值,并且俩者一样,这里比较就不用求出它。所以直接省去p(thew)
那么下面我们分别求p(thew|thaw)与p(thew|the)的大小比较与p(thaw)和p(the)的大小比较。
我们在这里用编辑距离和操作难度联合起来求解P(他实际输入的单词|我们猜测他想输入的单词),也就是p(thaw|thew)与p(the|thew)。
距离越近可能性越大,可以理解为,单词最容易输错成为同等长度或者长度相差不大的单词,在本问题中,然而 the 和 thaw 离 thew 的编辑距离都是 1,在这里我们 认为编辑距离对区分俩者没有区分度。
这时候需要考虑操作难度的大小,即去比较到底哪个更可能被错打称为thew。我们注意到字母 e 和字母 w 在键盘上离得很紧,无名指可能不小心就多打出一个 w 来,the 就变成 thew 了。
而另一方面 thaw 被错打成 thew 的可能性就相对小一点,因为 e 和 a 离得较远而且使用的指头相差一个指头(神经科学的证据表明紧邻的身体设施之间容易串位)。所以我们最终得到:
P(thew|thaw) < P(thew|the)
好的,我们已经得到了P(thew|thaw) < P(thew|the)。
下面我们来计算p(thaw)与p(the)的概率。
此时我们只需要比较thaw与the在文本库的出现频率。哪个频率高,我们就认为谁的概率大。
我们容易得出在英语中,the 出现的概率远远高于 thaw ,所以p(the)>p(thaw)
根据上面,我们可以得到
p(thaw)<p(the),p(thew|thaw)<p(thew|the)
则我们可以得出结论:
p(thew|thaw)*p(thew|thaw)<p(thew|the)*p(the)
那么我们可以认为,用户其实想敲入的是the这个词语。
于是根据上面,我们详细的走了一遍朴素贝叶斯算法的例子,虽然这个算法用在单词纠错上的准确率不是太高。
但是至少让我们清清楚楚的看到了数学算法在实际中是如何应用的。我相信不要陷入抽象的公式,跳出来实际应用这点很重要。
希望对大家理解有帮助~
参考文献:
1.周志华 《机器学习》 清华大学出版社
2.吴军 《数学之美》人民邮电出版社
3.刘丹,方卫国,周泓 《基于贝叶斯网络的二元语法中文分词模型》
推荐阅读文章:
近期文章预告:
《深入浅出决策树算法》
《深入浅出最大熵模型》
《深入浅出支持向量机》
.