重版朴素贝叶斯与拣鱼的故事

Posted 2021-04-25 夕小瑶的卖萌屋

重版公告

由于小夕之后要讲的好几篇文章要基于这一篇的知识，但是以前写的的这篇文章对朴素贝叶斯的讨论不够深入，又不值得再额外写一篇朴素贝叶斯啦，因此本文重版了以前的文章《朴素贝叶斯》。与旧版相比，新版对基础知识的讲解进行了大幅更新，并加入了一些更深的讨论和结论，并重新进行了排版。

朴素贝叶斯分类器可以说是最经典的基于统计的机器学习模型了。首先，暂且不管贝叶斯是什么意思，朴素这个名字放在分类器中好像有所深意。

一查，发现这个分类器的英文是“Naïve Bayes”。Naïve（读作“哪义务”）即幼稚的、天真的（但是总不能叫“幼稚贝叶斯”阿），Bayes即贝叶斯。那么这里的Naïve/朴素，是什么意思呢？其实就是代表着简化问题复杂度，像一个小孩子一样，不考虑复杂的东西。

Naive

一句话描述Naïve的意思就是“特征独立性假设”。详细的说，这里的独立性假设一般是指“条件独立性假设“，但是在处理序列问题时（比如文本分类、语音识别），还经常用到“位置独立性假设”，分别是什么意思呢？

条件独立性假设 {

如果我们要识别一个人的性别，要用到“身高”和“体重”这两个特征。所以这里的类别y为男/女，特征X=[x1=身高  x2=体重]。

我们知道，“身高”和“体重”明明是有关系的，比如身高1米8的人是不太可能体重低于100斤的，但是在朴素贝叶斯分类器的眼里，身高和体重没有关系。即令 x1=身高为180cm ， x2=体重为50kg ，则：

意思即一个人身高为180cm且体重为50kg的概率就等于一个人为180cm的概率乘以一个人为50kg的概率。虽然一个人为180cm的概率很大（比如一个男孩子），一个人为50kg的概率也很大（比如一个女孩子），但是人的身高为180cm且体重为50kg的概率很小。但是在贝叶斯的条件独立性假设下，x1与x2相互独立，故是直接将和这两个大概率相乘的，故算出来的概率肯定远大于实际值。

总结，朴素贝叶斯模型会假设特征向量的各个维度间相互独立（毫无关系）。即“条件独立性假设”。

}

位置独立性假设{ 

位置独立性假设一般不会提，但是如果要用朴素贝叶斯模型解决序列化的分类问题时，就必须引入这个假设了。

位置独立性的意思是对于序列中各个位置的特征向量，完全忽略其位置信息。举个栗子，比如在文本挖掘中，“我|喜欢|狗”中有三个特征向量，即分别为向量“我”、向量“喜欢”、向量“狗”，如果我们按照先后顺序来考虑这三个特征的话，就能得出你喜欢狗这个事实。但是如果按照“狗”“喜欢”“我”这样的顺序的话，得到的意思就完全变了。显然，这里各个特征向量之间的先后顺序（即位置）对于语义相关的分类任务而言是很重要的。然而，朴素贝叶斯的假设就是位置之间是独立的，即完全抛弃序列的位置信息。因此在朴素贝叶斯看来，“我|喜欢|狗”与“狗|喜欢|我”是同一个分类任务。

}

 

好，朴素的意思我们懂了，那么核心就是贝叶斯了。

Bayes

显然，在统计理论中，与贝叶斯最相关的就是贝叶斯定理，也叫贝叶斯公式。不用管能不能看懂，先贴出通用形式的公式：

 

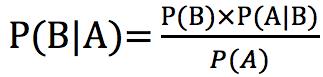
我们把公式里的事件A看作样本特征为某值，该值用X表示。把B看作分类目标的类别为某值，该值用y表示。然后就会发现非常非常简单啦，如下：

所以呢，这个公式的意思就是：

公式左边：已知样本特征的值为X的情况下，目标类别为y的概率（即，专业说法叫后验概率）就等于

公式右边：什么都不知道的情况下，目标类别为y的概率（即，专业说法叫类别y的先验概率）乘以已知目标类别是y的情况下，特征的值为X的概率（即，专业说法叫似然函数）。再除以什么都不知道的情况下，特征的值为X的概率（即，专业说法叫特征X的先验概率，也有的叫证据)。

 

诶？细心的读者有没有发现什么呢？相信此时肯定已经有人激动了！我们这里看一个栗子，引入更深的讨论。

 

就是这个栗子。

 

 

其实是下面的栗子啦(￣∇￣)。

 

假如小夕捕获了一批鱼，这批鱼中只有黑鱼和三文鱼。虽然小夕并不认识这两种鱼，但是小夕有设备可以测量出每条鱼肚皮的亮度等级（比如最白为10级，最黑为1级）。然后有一位好心的粉丝送给了小夕一批标好类别的黑鱼和三文鱼。那么小夕借助上面这些已经知道的东西，用朴素贝叶斯分类器来给小夕捕的那些鱼的类别贴标签，从而分拣出三文鱼和黑鱼，要怎么做呢？

拣鱼

诶？这里不是说鱼肚皮的亮度等级都能测出来嘛？那鱼肚皮的亮度等级不就是一个特征咯，每条鱼测出来的亮度等级不就是特征的值嘛，即X。而黑鱼和三文鱼就是我们要分类的目标，记为类别c0和类别c1。有没有灵光一现？

对！还记得贝叶斯定理的等式左边的的意思吗？假如某条鱼测得的亮度等级为2，那么我们只需要计算并比较  与  的大小不就可以啦！肯定是值更大的，也就是概率更大的，就是我们要输出的类别呀！专业说法叫取最大后验概率。

 

那么怎么计算呢？显然就是用等式右边那三坨（噗，好不文明的说）。为了方便阅读，在这里再贴一遍。

 

 

首先，右边这三坨中，除号底下的代表特征取某值的概率，然而我们要预测某一条鱼的类别，显然这条鱼的特征的值我们已经知道了，即定值，因此不管是求  也好，求   也好，  是相同的值，对于比较这两个概率的大小没有任何帮助。因此干脆不计算了。

然后，这三坨中的  代表某类别的先验概率，怎么计算得到呢？还记得粉丝给了小夕一堆鱼吗？那我们直接用这一堆鱼来近似得到  不就可以啦！

按照概率论的大数定律的意思，当样本足够多时，样本的统计比率就可以近似真实概率。回想一下抛10000次均匀硬币时会有接近5000次正面向上，由此得到正面向上的概率为0.5

因此，假如粉丝给了小夕10000条鱼，其中3000条是黑鱼，7000条是三文鱼，那显然  ，同理  。看， 解决了吧。

 

三坨中的最后一坨，  怎么得到呢？也很轻松啊，同样是利用粉丝给的10000条鱼，小夕用设备将这10000条鱼的亮度等级测出来后，只需要从每个类别的鱼群中，统计一下特征X的每个取值下的鱼数量占该类别的鱼总数的比率就好啦。

比如黑鱼有3000条，其中亮度等级为8的鱼一共有1000条，那么  。同理可以得到其他  的值啦。

 

至此，等式右边全都解决了，因此等式左边也能比较大小了。所以对于下面这种情况的话（粉丝给了小夕100来条鱼用于训练分类器）：

 

 

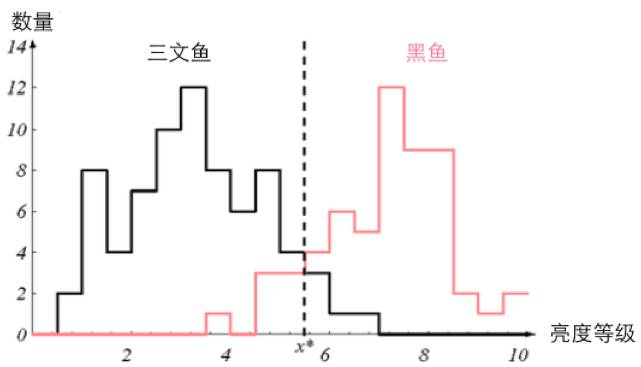
小夕做好的朴素贝叶斯分类器肯定会将亮度等级小于的鱼都认为是三文鱼（在此情况下，类别判定为三文鱼的概率总是比黑鱼的概率大），反之都认为是黑鱼。

等等，问题出现了，我们知道，的点就是与相等的点。但是，朴素贝叶斯在计算这两个值的时候，算出来的真的是这两个值吗？

到底是什么

还记不记得，前文中，我们在计算等式左边的时候，忽略了等式后边的这一项！再把公式搬过来：

也就是说，贝叶斯分类器在计算每个类别的“后验概率”的时候，实际上计算出的并不是后验概率！由于只计算了，因此得到的结果实际上是！！！

而是什么呢？有概率论基础的同学应该知道，这个就是y与X的联合概率，也就是，也就是X与y共同发生的概率。

所以说，朴素贝叶斯分类器的核心虽然是贝叶斯公式，但是其计算某样本的各类别的可能性时，实际上计算出的不是各类别的后验概率，而是各类别y与该样本特征X的联合概率！

这一结论有什么用呢？以后就有用啦~而且至关重要哦。

等等，还有个问题，到目前为止，都没有用到文章开头写的条件独立性假设啊？这个假设有什么用呢？

多维特征

当然啦，这个假设本质上的意思就是忽略X各个维度之间的相关性，因此当X有多维特征时，就派上用场啦。

比如小夕又买了个尺子，可以测量鱼身的长度。

 

这时特征 X=[x1(亮度) x2(身长)] 了。这时唯一的影响就是在计算等式右边的这个  时，按照独立性假设展开成  就可以啦。看吧，naïve一些还是可以避免很多麻烦的。