朴素贝叶斯-最适合简单的文本分析的方法

Posted 2021-04-25 赛博坦视觉

目录

1. 定义

2. 演示

            2.1 以垃圾邮件分类为例子

            2.2 文本表示

                    2.2.1 单词的表示

                    2.2.2 句子的表示

3. 代码

============================================================================

1.定义

贝叶斯方法是以贝叶斯原理为基础，使用概率统计的知识对样本数据集进行分类。朴素贝叶斯算法（Naive Bayesian algorithm) 是应用最为广泛的分类算法之一。

2. 演示

  2.1 以垃圾邮件分类为例子

朴素贝叶斯在分类的时候，需要计算很多概率，所需要计算的概率下面一一进行演示。如下图所示，我们已知有24封正常邮件，12封垃圾邮件。我们要根据已知的数据，来对新的一封邮件进行分类。

我们最终的目的是要计算出P（垃圾|新邮件）和P（正常|新邮件）这两个概率来进行比较。如果P（垃圾|新邮件）> P（正常|新邮件），则将新邮件定为垃圾邮件。

要计算P（垃圾|新邮件）和P（正常|新邮件），则需要计算出垃圾和正常额先验概率和邮件中每个单词出现在垃圾邮件或者正常邮件中的概率。计算公式如下：

其中P（邮件内容|垃圾）=P（单词1|正常）×P（单词2|正常）×P（单词3|正常）......

从上面的公式可以看出，我们需要就算出先验概率P（垃圾）和P（正常），以及P（邮件内容|垃圾）和P（邮件内容|正常）。分母P（邮件内容）对结果比较没有影响，因为最终的两个概率分母相同。

如下图，总共36封邮件，则先验概率P（垃圾）= 1/2，P（正常）= 2/3。

图中标黄的邮件代表购买这个词在该邮件中出现，上面也标了出现的次数。假设每封邮件包含10个单词， 则:

P（购买|正常）=3/（24*10）= 1/80

P（购买|垃圾）=3/（12*10）= 7/120

同样，我们要计算出所有的P（单词|垃圾）和P（单词|正常），这里的单词为出现在垃圾邮件和正常邮件中的所有单词。

Note：在计算的过程中，可能会出现某个词在垃圾短信中存在，而不存在于正常短信中，这样会导致存在一个P（某单词|正常）=0，最终导致P（正常|新邮件）=0，这显然是不合理的。为了避免这一现象，我们需要进行平滑操作，即在求P（某单词|正常）和在求P（某单词|垃圾）的时候，分母加单词个数V，分子加1。如：

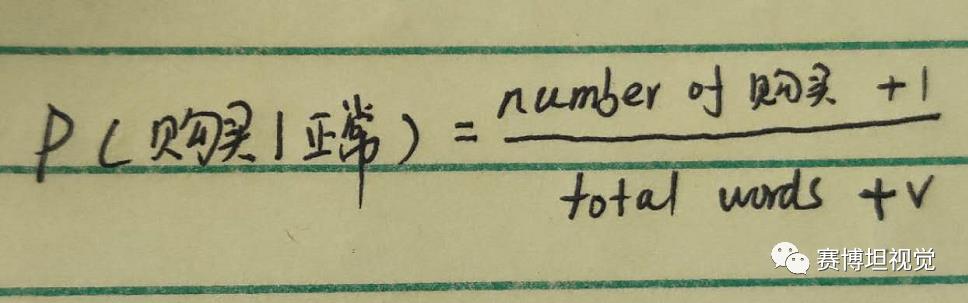
下面手推一个完整的例子：

如下，假设我们有垃圾邮件3封，正常邮件3封，然后来预测新邮件是垃圾邮件还是正常邮件。

具体计算细节如下图：

2.2 文本表示

2.2.1 每个单词的表示

假设有一个词典=[我们，去，爬山，今天，你们，昨天，跑步]总共7个单词，则他们需要分别表示为：

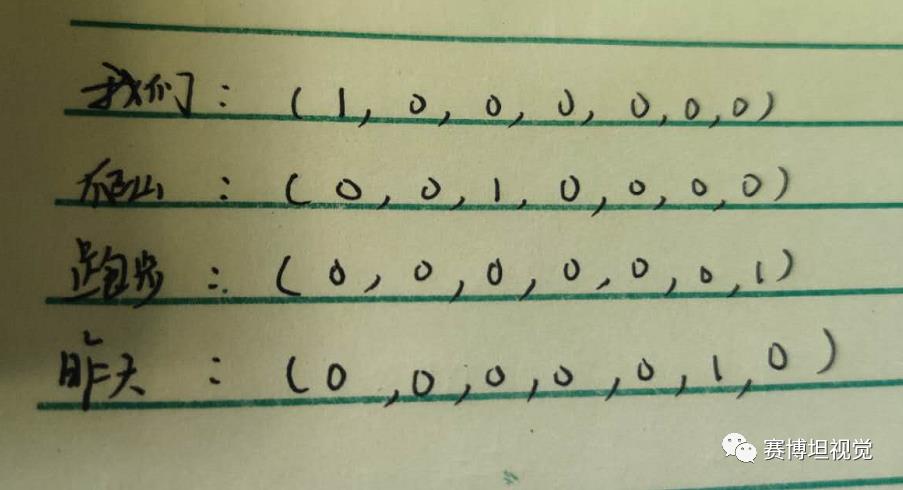
2.2.2 句子表示

常见的句子表示有3种，布尔法，计数法和tfidf法。依然假设有一个词典=[我们，又，去，爬山，今天，你们，昨天，跑步] 我们用3中方法分别表示下面3个句子：

详细表示如下图：

以上是布尔法和计数法，然而这2种方法存在很大的缺点。常用的是tfidf法。

3.代码

# 读取spam.csv文件import pandas as pddf = pd.read_csv("data_spam/spam.csv", encoding='latin')df.head()
# 重命名数据中的v1和v2列，使得拥有更好的可读性df.rename(columns={'v1':'Label', 'v2':'Text'}, inplace=True)df.head()
# 把'ham'和'spam'标签重新命名为数字0和1df['numLabel'] = df['Label'].map({'ham':0, 'spam':1})df.head()
# 统计有多少个ham，有多少个spamprint ("# of ham : ", len(df[df.numLabel == 0]), " # of spam: ", len(df[df.numLabel == 1]))print ("# of total samples: ", len(df))
# 统计文本的长度信息text_lengths = [len(df.loc[i,'Text']) for i in range(len(df))] print ("the minimum length is: ", min(text_lengths))
import numpy as npimport matplotlib.mlab as mlabimport matplotlib.pyplot as plt
plt.hist(text_lengths, 100, facecolor='blue', alpha=0.5)plt.xlim([0,200])plt.show()

# 导入英文呢的停用词库from nltk.corpus import stopwordsfrom sklearn.feature_extraction.text import CountVectorizer# what is stop wordS? he she the an a that this ...stopset = set(stopwords.words("english"))
# 构建文本的向量 （基于词频的表示）#vectorizer = CountVectorizer(stop_words=stopset,binary=True)vectorizer = CountVectorizer()
# sparse matrix X = vectorizer.fit_transform(df.Text)y = df.numLabel
# 把数据分成训练数据和测试数据from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=100)print ("训练数据中的样本个数: ", X_train.shape[0], "测试数据中的样本个数: ", X_test.shape[0])
# 利用朴素贝叶斯做训练from sklearn.naive_bayes import MultinomialNBfrom sklearn.metrics import accuracy_score

clf = MultinomialNB(alpha=1.0, fit_prior=True)clf.fit(X_train, y_train)y_pred = clf.predict(X_test)print("accuracy on test data: ", accuracy_score(y_test, y_pred))
# 打印混淆矩阵from sklearn.metrics import confusion_matrixconfusion_matrix(y_test, y_pred, labels=[0, 1])