迷宫寻路系列常用算法逻辑探究
Posted GameRes游资网
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了迷宫寻路系列常用算法逻辑探究相关的知识,希望对你有一定的参考价值。
前言:
又到了人才流动的高峰季节,“金三银四”,过了这个村,就没那个店,面试者勤奋地准备题典,面试官也在奋笔疾书, 有些面试官喜欢广度的知识覆盖,而有些面试官喜欢深度的知识探求。
笔者不是面试者,也不面试官,但想结合自身的学习和工作经历,对深度型的题材做下尝试和研究。
这篇让我们谈谈迷宫寻路系列,分基础篇,进阶篇和难度篇。
基础篇:
让我们先来构造一个游戏场景:
在一个迷宫中,鼠精灵需要绕过巨石,找到迷宫中的出口,求最短路径?

关于该问题,大家肯定不假思索的提到: 宽度优先遍历(BFS)。
// 1).初始化工作
// 1.1). 把源节点坐标放入队列中
queue.push((x, y,step=0));
// 1.2). 标示该节点访问过
visited[(x, y)] = true
// 2).BFS procedure
while ( !queue.empty() ) {
// 2.1).取出当前节点
(x, y, step) <= queue.pop()
// 2.2).判断是否为目标节点, 并返回
if ( (x, y) == (dest.x, dest.y) ) {
return (step);
}
// 2.3).遍历(x, y)的邻近节点
foreach ((x', y') in neighbor(x, y)) {
// 2.3.1).可到达且没有访问过
if (is_available(x', y') and visited[(x, y)] == false) {
queue.push((x', y', step + 1));
// 标示访问过
visited[(x', y')] = true
}
}
}
// 3). 不存在路径
return unavailable
注: 判断是否到达目标节点的代码片段比较灵活, 为了加速可放到2。3。1) IF判断里面。
确实很简单,不过这是最基本的。
进阶篇:
同样的场景,如果迷宫很大,那使用BFS的话,效果就不是很高。那是否存在更高效的算法呢?
有两种成熟而常规的实现思路: A*算法和双向宽度优先搜索。
1)A*算法:
该算法引入启发式评估函数,用以加速最短路径求解过程。
核心概念:
历史代价g(n): 从初始节点到n节点的实际代价,代表过去和现在
预测评估h(n): 当前节点n到目标节点的预测代价,代表未来
启发评估f(n): 节点n的估价函数,其满足f(n) = g(n) + h(n)
这边特别要注意的一个先决条件:预测函数h(n)<= 实际的真实代价
预测函数h(n)越接近于真实代价,其启发评估的效果越好。
更详细的请参考如下博文“Amit's A star Page中译文”。
这边我们选择曼哈顿距离作为预测函数h(n),整体的框架代码如下:
// 1).初始化工作
// 1.1). 把源节点坐标放入优先队列中
priority_queue.push((x, y, f(x,y)=0));
// 1.2). 标示(x, y)的代价为0, 其余皆为无限大
cost[(x, y)] = (f(x, y) = 0)
// 2).BFS procedure
while ( !priority_queue.empty() ) {
// 2.1).取出当前节点
(x, y, f(x,y)=step) <= priority_queue.pop()
// 过滤掉中间节点
if ( f(x,y) > cost[(x, y)] ) {
continue;
}
// 2.2).判断是否为目标节点, 并返回
if ( (x, y) == (dest.x, dest.y) ) {
return f(x, y);
}
// 2.3).遍历(x, y)的邻近节点
foreach ((x', y') in neighbor(x, y)) {
// 可到达且节点有更优的解
g(x',y') = f[(x, y)] + 1;
if ( is_available(x', y') and (cost[(x', y')] > g(x',y') + h(x', y')) ) {
priority_queue.push((x', y', f(x',y')=g(x',y')+h(x',y')));
// 更新该节点的评估值
cost[(x', y')] = f(x',y')=g(x',y')+h(x',y')
}
}
}
// 3). 不存在路径
return unavailable
注: 于BFS版相比,这边使用优先队列代替FIFO的队列,并借助代价cost表代替访问visited表。
2)双向宽度优先遍历:
该算法借助起点和终点的双向宽度遍历,来加速最短路径的求解过程。
算法的流程和代码就不再具体展开了,让我们通过画图来形象地比较各个算法的优劣。
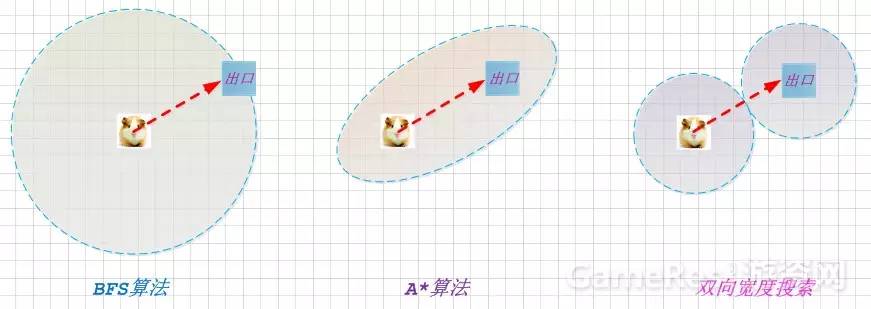
寻路算法遍历的节点数量,可用面积来表示。图中可得BFS是圆型,A*是椭球型,而双向宽度搜索则是两个刚好相切的圆形。从图形面积对比中,我们可以获取到各个算法优劣的视觉直观体验。
难度篇:
之前的场景比较普通,现在让我们加入小怪兽来搅搅局。
在新的场景中,小怪兽按固定线路在巡视,鼠精灵需要走出迷宫的最少耗时是多少?“最短路径”是多少?
在有不确定的因素的干扰下,使用常规的最短路径算法就不再可行的。有没有其他的解法呢?
在迷宫地图较小时,我们可以借助动态规划的思想来解决。
设opt[n][y][x]为状态矩阵:
n表示步数, (x, y)表示迷宫地图的位置信息, 而其值表示鼠精灵在该步数后能否到达该节点.
初始状态:
opt[0][y][x] = true
状态迁移方程:
opt[n+1][y][x] = (opt[n][y'][x']==true && monster[n+1] != (x', y') )==false, {ε(x',y'),adjacency to (x,y)}) ? true : false;
具体的伪码如下:
// 初始化
opt[0][y][x] = true;
// 步数遍历
for ( step = 0; ; step++ ) {
// 迷宫矩阵遍历
for ( i = 0; i < height; i++ ) {
for ( j = 0; j < width; j++ ) {
// 当前节点可达
if ( opt[step][i][j] == true ) {
// 枚举各个邻近的可达节点
foreach (x', y') adjacency (j, i) {
// 小怪兽在步数step + 1, 没有走到该点
if ( monster[step + 1] != (x', y') ) {
opt[step + 1][y'][x'] = true;
}
}
}
}
}
// 检查目标节点是否到达
if ( opt[step][dest_y][dest_x] == true ) {
return step;
}
}
return Oops;
注: 若该迷宫没解,必然存在循环节,最外层循环借助滚动数组来优化。
总结:
从迷宫寻路的场景出发,逐步进行基础知识的深挖掘,还是具备一定的区分度的。
面试这东西,能遇到一个nice的面试官是种幸福。但很多时候,往往是一场闹剧了。
以上是关于迷宫寻路系列常用算法逻辑探究的主要内容,如果未能解决你的问题,请参考以下文章