人工智能的算法基础篇常用算法和背景知识介绍

Posted 2021-04-20 夏日晴天

何为算法（algorithm）？来一段维基百科

In mathematics and computer science, an algorithm (/ˈælɡərɪðəm/ (listen)) is an unambiguous specification of how to solve a class of problems. Algorithms can perform calculation, data processing, and automated reasoning tasks.

As an effective method, an algorithm can be expressed within a finite amount of space and time and in a well-defined formal language for calculating a function.Starting from an initial state and initial input (perhaps empty), the instructions describe a computation that, when executed, proceeds through a finite number of well-defined successive states, eventually producing "output" and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.

The concept of algorithm has existed for centuries. Greek mathematicians used algorithms in, for example, the sieve of Eratosthenes for finding prime numbers and the Euclidean algorithm for finding the greatest common divisor of two numbers.

In computer systems, an algorithm is basically an instance of logic written in software by software developers, to be effective for the intended "target" computer(s) to produce output from given (perhaps null) input. An optimal algorithm, even running in old hardware, would produce faster results than a non-optimal (higher time complexity) algorithm for the same purpose, running in more efficient hardware; that is why algorithms, like computer hardware, are considered technology.

计算机科学中的算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

说算法之前要先找到一个定位，推荐李航的《统计学习方法》本文摘录了书中的一些内容，由于他的书2012年就出版了，主要是针对监督学习后面我又补充了深度学习的一些算法内容介绍。

背景知识统计学

了解算法就不得不要多展开一点背景知识，就是统计学。这是非常重要的一门学科，也是大数据应用的基础学科和数据分析的重中之重。在合理应用统计学理论的基础上，我们可以解决很多日常生产中绝大多数数据释义问题包括计算机编程。

以下内容部分摘自李航的《统计学习方法》整理而成。

       在计算科学领域中，统计学习 (statistical learniog) 是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一 门学科． 统计学习也称为统计机器学习 (statistical machine learning) 。

统计学习的主要特点是

(1)统计学习以计算机及网络为平台，是建立在计算机及网络之上的；

 (2)统计学习以数据为研究对象，是数据驱动的学科；

 (3)统计学习的目的是对数据进行预测与分析； 

(4)统计学习以方法为中心， 统计学习 方法构建模型并应用模型进行预测与分析； 

(5)统计学习是概率论、统计学、 信息论、 计算理论、最优化理论及计算机科学等多个领域的交叉学科， 并且在发展 中逐步形成独自的理论体系与方法论。

赫尔伯特·西蒙 (Herbert A. Simoo) 曾对 “学习“ 给出以下定义：

“如果一个系统能够通过执行某个过程改进它的性能， 这就是学习．”按照这一观点， 统计学习就是计算机系统通过运用数据及统计方法提高系统性能的机器学习．

现在，当人们提及机器学习时，往往是指统计机器学习

 统计学习的对象

统计学习的对象是数据 (data). 它从数据出发， 提取数据的特征， 抽象出数据的模型，发现数据中的知识，又回到对数据的分析与预测中去．作为统计学习的对象，数据是多样的， 包括存在千计算机及网络上的各种数字、文字、 图像、 视频、音频数据以及它们的组合．

统计学习关于数据的基本假设是同类数据具有一定的统计规律性， 这是统计学习的前提．这里的同类数据是指具有某种共同性质的数据， 例如英文文献、 互联网网页、数据库中的数据等．

统计学习用于对数据进行预测与分析，特别是对未知新数据进行预测与分 析．对数据的预测可以使计算机更加智能化，或者说使计算机的某些性能得到提高；对数据的分析可以让人们获取新的知识，给人们带来新的发现．

对数据的预测与分析是通过构建概率统计模型实现的．

统计学习总的目标

就是考虑学习什么样的模型和如何学习模型，以使模型能对数据进行准确的预测与 分析，同时也要考虑尽可能地提高学习效率．

统计学习的方法

统计学习的方法是基于数据构建统计模型从而对数据进行预测与分析．统计 学习由监督学习(supervisedlearning)、非监督学习(unsupervisedlearning)、半监 督学习(semi-supervisedlearning)和强化学习(reinforcementlearning)等组成．

监督学习，这种情况下统计学习的方法可以概括如下：从给定 的、有限的、用于学习的训练数据(trainingdata)集合出发，假设数据是独立同分布产生的；并且假设要学习的模型属于某个函数的集合，称为假设空间(hypothesis space), 应用某个评价准则(evaluationcriterion), 从假设空间

中选取一个最优的 模型，使它对已知训练数据及未知测试数据(testdata)在给定的评价准则下有最优的预测；最优模型的选取由算法实现．这样，统计学习方法包括模型的假设空 间、模型选择的准则以及模型学习的算法，称其为统计学习方法的三要素，简称 为模型(model)、策略(strategy)和算法(algorithm).

实现统计学习方法的步骤如下；

(1)   得到1个有限的训练数据集合

(2) 确定包含所有可能的模型的假设空间，即学习模型的集合；

(3) 确定模型选择的准则，即学习的策略；

(4) 实现求解最优模型的算法，即学习的算法；

(5) 通过学习方法选择最优模型；

(6) 利用学习的最优模型对新数据进行预测或分析．

统计学习的目的

统计学习用于对数据进行预测与分析，特别是对未知新数据进行预测与分 析．对数据的预测可以使计算机更加智能化，让人们获取新的知识，给人们带来新的发现．

对数据的预测与分析是通过构建概率统计模型实现的．统计学习总的目标就 是考虑学习什么样的模型和如何学习模型，以使模型能对数据进行准确的预测与 分析，同时也要考虑尽可能地提高学习效率．

统计学习的研究

统计学习研究一般包括统计学习方法(statisticallearning method)、统计学习 理论(statistical learning theory)及统计学习应用(application of statistical learning) 三个方面统计学习方法的研究旨在开发新的学习方法；统计学习理论的研究在 于探求统计学习方法的有效性与效率，以及统计学习的基本理论问题；统计学习 应用的研究主要考虑将统计学习方法应用到实际问题中去，解决实际问题.

统计学习的重要性

近20年来，统计学习无论是在理论还是在应用方面都得到了巨大的发展，有许多重大突破，统计学习已被成功地应用到人工智能、模式识别、数据挖掘、自然语言处理、语音识别、图像识别、信息检索和生物信息等许多计算机应用领域 中，并且成为这些领域的核心技术人们确信，统计学习将会在今后的科学发展和技术应用中发挥巨大作用。

统计学习是计算机智能化的有效手段,智能化是计算机发展的必然趋势，也是计算机技术研究与开发的主要目标。人工智能等领域的研究表明，利用统计学习模仿人类智能的方法，虽有一定的局限性，但仍然是最有效的手段。

统计学习三要素

下面论述以监督学习为例介绍统计学习三要素（非监督学习、强化学习也同样拥有 这三要素）．可以说构建一种统计学习方法就是确定具体的统计学习三要素．

统计学习方法都是由模型、策略和算法构成的，即统计学习方法由三要素构 成，可以简单地表示为

方法＝模型＋策略＋算法

构建一种统计学习方法就是确定具体的统计学习三要素．

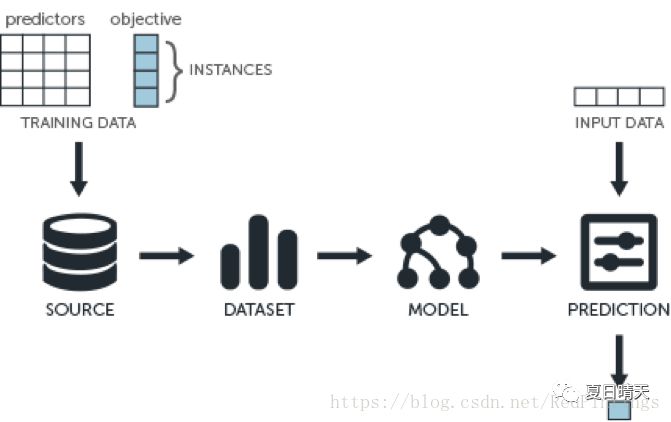
在监督学习过程中，模型就 是所要学习的条件概率分布或决策函数．模型的假设空间(hypothesisspace)包含所有可能的条件概率分布或决策函数．例如，假设决策函数是输入变量的线性 函数，那么模型的假设空间就是所有这些线性函数构成的函数集合．假设空间中 的模型型一般有无穷多个

假设空间用F表示．假设空间可以定义为决策函数的集合

F={fIY=f(X)}

其中，X和Y是定义在输入空间X和输出空间Y上的变量．这时F通常是由一个 参数向量决定的函数族：

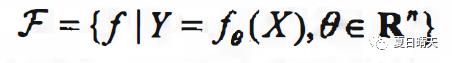
人工智能中重要的算法

再谈谈非监督学习算法人工智能算法中比较著名的有

多伦多大学计算机系教授Geoffrey Hinton是Deep Learning的开山鼻祖，于2006年提出深度学习的概念。基于深度置信网络(DBN)提出非监督贪心逐层训练算法，为解决深层结构相关的优化难题带来希望，随后提出多层自动编码器深层结构。此外Lecun等人提出的卷积神经网络是第一个真正多层结构学习算法，它利用空间相对关系减少参数数目以提高训练性能。 [1]

上图为Geoffrey Hinton

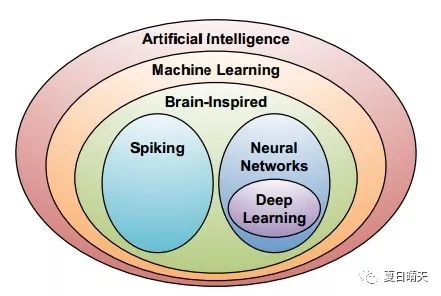
深度学习的概念源于人工神经网络的研究。含多隐层的多层感知器就是一种深度学习结构。深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据的分布式特征表示。 

From Wikipedia, the free encyclopedia

For deep versus shallow learning in educational psychology, see Student approaches to learning. For more information, see Artificial neural network.

Deep learning (also known as deep structured learning or hierarchical learning) is part of a broader family of machine learning methods based on learning data representations, as opposed to task-specific algorithms. Learning can be supervised, semi-supervised or unsupervised.^[1][2][3]

Deep learning architectures such as deep neural networks, deep belief networks and recurrent neural networks have been applied to fields including computer vision, speech recognition, natural language processing, audio recognition, social network filtering, machine translation, bioinformatics, drug design, medical image analysis, material inspection and board game programs, where they have produced results comparable to and in some cases superior to human experts.^[4][5][6]

Deep learning models are vaguely inspired by information processing and communication patterns in biological nervous systems yet have various differences from the structural and functional properties of biological brains (especially human brains), which make them incompatible with neuroscience evidences.^[7][8][9]

深度学习本质还是机器学习模型，只是思路和传统机器学习需要提取特征，然后建立模型学习，其中特征是人工提取的，深度学习可以不需要提取特征，采取无监督特征学习。受打哪神经元工作模式启发，提出的人工神经网络通过多年的发展非线性模型，其中BP神经网络就是最经典的一个模型。

多层网络的训练需要一种强大的学习算法，其中BP（errorBackPropagation）算法就是成功的代表，它是迄今最成功的神经网络学习算法。

今天就来探讨下BP算法的原理以及公式推导吧。

神经网络

　　先来简单介绍一下神经网络，引入基本的计算公式，方便后面推导使用

1 神经网络神经元模型

　　图1就是一个标准的M-P神经元模型。

【神经元工作流程】

　　每个神经元接受n个（图1中只有3个）来自其他神经元或者直接输入的输入信号（图1中分别为x0,x1,x2），这些输入信号分别与每条“神经”的权重相乘，并累加输入给当前神经元。每个神经元设定有一个阈值θ（图1中的b），累计值需要减去这个阈值，并且将最终结果通过“激活函数”（图1中的f）挤压到（0,1）范围内，最后输出。

　　总结一下，神经元的工作流程主要有3步：

　　①累计输入的信号与权重。

　　　　

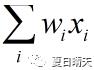
　　②将权重与设定的阈值相减

　　     

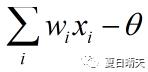
　　③将第2步得出的结果送给激活函数（一般是sigmoid函数），输出

          

 

【多层前馈神经网络】

　　将上面的神经元按照一定的层次结构连接起来，就得到了神经网络。

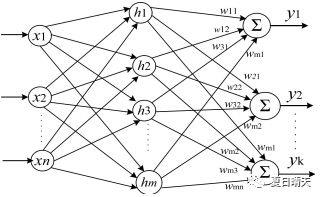
  图2 多层前馈神经网络

 

　　图2显示的是一个3层（1个输入层，1个隐藏层，1个输出层）的神经网络。

　　像这样的形成层级结构，每层神经元与下一层神经元全连接（每层的每个神经元到下一层的每个神经元都有连接），神经元之间不存在同层连接，也不存在跨层连接的神经网络通常被称为“多层前馈神经网络”。

【神经网络工作流程】

　　假定有数据集D:

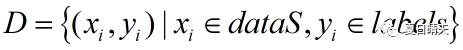
　　输入神经网络，同样假定就是图2这个3层前馈神经网络，我们来列一下，图2这个网络要通过这些训练集来训练得到多少个参数。

　　图2的神经网络有n个输入神经元（记为x1、x2....xn）、m个隐藏层神经元（记为h1,h2,...,hm），k个输出神经元（记为y1,y2,...,yk），通过训练，我们要获得下面几种数值

　　①输入层到隐藏层的权值：n x m 个

　　②隐藏层到输出层的权值：m x k 个

　　③m个隐藏层阈值与k个输出层阈值

　　训练完成后，通过测试集样例与训练出的参数，可以直接得到输出值来判断所属分类（分类问题）

BP算法

　　神经网络的运行过程清楚了，那么训练过程是怎么样的呢？

　　我们知道，训练的任务是：

　　　　　　通过某种算法，习得上面所讲的n x m + m x k + m + k = (n+k+1) x m + k 个参数

　　这里我们使用的就是BP算法。

　　先来根据神经元工作流程来定义几个量，这里再贴一下修改后的神经网络流程图

图3 3层前馈神经网络图

【定义】

　　　　第i个输入神经元到第j个隐藏层神经元的权重:Vij

　　　　第i个隐藏层神经元到第j个输出层神经元的权重:Wij

　　　　第i个隐藏层神经元的输出：bi

　　　　第i个输出层的阈值:θi

　　　　第j个隐藏层神经元的输入：

　　　　　　　　  

　　　　第q个输出神经元的额输入：

　　　　　　　　　

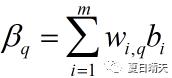
　　假定通过我们的神经网络，对于训练样例网络输出为

　　 假定完美输出应该为，例如，对于k分类问题，若训练样例p属于第1类，则yp=(1,0,0,0...,0)

　　那么一轮训练我们的均方误差为：

　　

　　实际上

　　其中f函数为sigmoid函数。

　　这下，我们的目标就转化为：

　　　　寻得一组合适的参数序列，使得(1)式的值（均方误差）最小。

　　在我的上一篇随笔里也提到过这个问题，这种形式的问题比较适合使用梯度下降算法，BP正是采取了这个策略，以目标的负梯度方向对参数进行调整。

【梯度下降求解参数】

　　梯度下降的基本思想是：设定参数的初始值，通过一个学习速率η和当前梯度，来逐渐步进参数，以求拟合一个局部最优的参数

　　一般的参数迭代过程如下：

　　　　

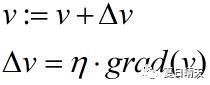
　　不清楚梯度下降算法的可以看一下我另一篇随笔：http://www.cnblogs.com/HolyShine/p/6403116.html

　　神经网络的一次迭代，就是参数的一次“步进”。

　　接下来我们使用梯度下降分别推导几个参数的迭代公式

　　我们以隐藏层中第h个神经元为参照对象，求解他的输入权重V和输出权重W，以及阈值γ；以输出层中第j个神经元为输出参照，求解他的阈值θ

 　　<隐藏层到输出层的权重Whj>

　　根据梯度下降算法，权重参数的步进为：

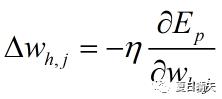
　　由复合函数求导公式以及式（1）式（2）：

　　其中，第二项是sigmoid函数求导，由于sigmoid函数有如下的性质：

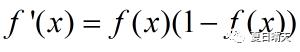
　　所以

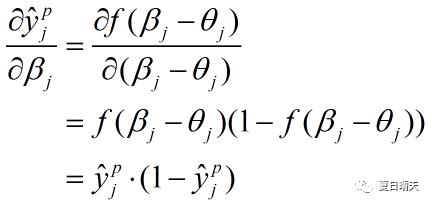
　　第一项和第三项的推导也列在这里

　　最终（3）式变为：

　　

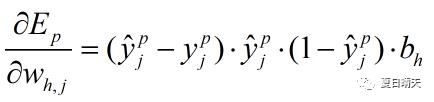
　　这些量都是一轮训练中已知的，因此可以解得梯度的大小，用于参数的更新工作

　　其他参数的求解基本一致。

 

数据科学中的算法

什么是数据科学？它和已有的信息科学、统计学、机器学习等学科有什么不同？作为一门新兴的学科，数据科学依赖两个因素：一是数据的广泛性和多样性；二是数据研究的共性。现代社会的各行各业都充满了数据，这些数据的类型多种多样，不仅包括传统的结构化数据，也包括网页、文本、图像、视频、语音等非结构化数据。

数据科学是一个多学科领域，专注于从大量原始和结构化数据中找到切实可行的见解。该领域主要注重发掘我们没有意识到我们还不清楚的事情的答案。数据科学专家使用几种不同的技术来获得答案，包括计算机科学，预测分析，统计学和机器学习，通过海量数据集进行解析，努力为尚未被认识到的问题提供解决方案。

数据科学主要包括两个方面：用数据的方法研究科学和用科学的方法研究数据。前者包括生物信息学、天体信息学、数字地球等领域；后者包括统计学、机器学习、数据挖掘、数据库等领域。这些学科都是数据科学的重要组成部分，只有把它们有机地整合在一起，才能形成整个数据科学的全貌。

数据科学能使用数字和名称（也称为类别或标签）预测问题的答案。

这可能会让人感到惊讶，但数据科学只可解答以下五种问题：

• 这是 A 还是 B？

• 这是否很奇怪？

• 多少？

• 组织方式为何？

• 接下来该怎样做？

以上每个问题都由单独系列的机器学习方法（称为算法）回答。

问题 1：“这是 A 还是 B？”使用分类算法

让我们从这个问题开始：这是 A 还是 B？

系列算法称为双类分类。

对于任何仅有两种可能答案的问题很有用。

例如：

• 此轮胎是否会在下一 1,000 英里中出现故障：是或否？

• 以下哪种方案可吸引更多顾客：5 美元优惠券或 25% 折扣？

此问题还可进行改述，来包括两个以上的选项：这是 A、B、C 还是 D，等？ 这称为多类分类，当有多个或数千个可能的答案时很有用。 多类分类选择可能性最大的一个答案。

问题 2：“这是否很奇怪？”使用异常检测算法

下一个数据科学可以回答的问题是：这是否很奇怪？ 此问题通过称为异常检测的算法系列进行回答。

如果有信用卡，那么已从异常检测获益。 信用卡公司分析购买模式，使他们可提醒用户可能的欺诈行为。 “异常”费用可能是在一家通常不会去购物的商店购物时，或购买非常昂贵的物品时所产生的费用。

此问题在很多方面都很有用。 例如：

• 如果汽车上配有压力表，可能会想知道：此压力表读数是否正常？

• 如果在监视 Internet，会想知道：此消息是否来自典型 Internet？

异常检测标志意外或异常事件或行为。 它会提供在何处查找问题的线索。

问题 3：“多少？”使用回归算法

机器学习还可以预测“多少？”这一问题的答案。 回答此问题的算法系列称为回归算法。

回归算法进行数字预测，例如：

• 下周二的气温是多少？

• 我第四季度销售额有多少？

它们可帮助回答任何寻求数字答案的问题。

问题 4：“组织方式为何？”使用聚类分析算法

最后两个问题更高级一点。

有时希望了解数据集的结构 - 组织方式为何？ 对于此问题，并没有已经知道结果的示例。

可通过多种方法梳理出数据结构。 其中一种方法就是聚类分析。 为方便解释，该方法将数据分成多个自然“群”。 使用聚类分析，不会存在正确答案。

聚类分析问题的常见示例有：

• 哪些观众喜欢同类型的电影？

• 哪些打印机型号出现故障的方式相同？

通过了解数据的组织方式，可以更好地了解并预测行为和事件。

问题 5：“现在应该做什么？”使用强化学习算法

最后一个问题 – 现在应该做什么？ - 使用称为强化学习的算法系列。

强化学习的灵感来自于老鼠和人类的大脑对惩罚和奖励的反应。 这些算法从结果中学习，并决定下一步操作。

通常，强化学习适用于自动系统，这些自动系统需要在没有人工指导的情况下做出大量小决策。

此算法总是用于回答此类问题：（通常指计算机或机器人）应采取何种操作。 示例如下：

• 如果我是房子的温度控制系统：调整温度还是保持原有温度？

• 如果我是自动驾驶汽车：遇到黄灯时，是刹车还是加速？

• 对于机器人吸尘器：继续吸尘或返回充电站？

强化学习算法在执行过程中收集数据，从试验和错误中学习。

这就是数据科学可以回答的 5 个问题。

将算法视为配方，数据视为成分可帮助理解。 算法告知如何组合以及混合数据以获取答案。 计算机如同搅拌机。 它们可快速完成算法的大部分繁琐工作。

       

斯坦福大学算法课资料：

https://web.stanford.edu/class/cs97si/

总结一下：

统计学习方法都是由模型、策略和算法构成的，即统计学习方法由三要素构 成，可以简单地表示为

方法＝模型＋策略＋算法

模型对应的数学公式，公式中往往有待学习得到的参数，因此在进行训练或者学习时，首先初始化这部分参数（0 或标准正太分布）； 

学习之前的初始化：initial model；

学习完成之后的模型：final model；

模型

计学习首要考虑的问题是学习什么样的模型．在监督学习过程中，模型就 是所要学习的条件概率分布或决策函数．模型的假设空间(hypothesisspace)包含所有可能的条件概率分布或决策函数．

算法则是一套处理的流程； 

引入新的记号（变量）；

对参数进行update；

算法执行结束，意味着最终的参数也学习得到；

策略，有了模型的基础上按照什么样的准则学习或选择最优的模型和适合的算法；

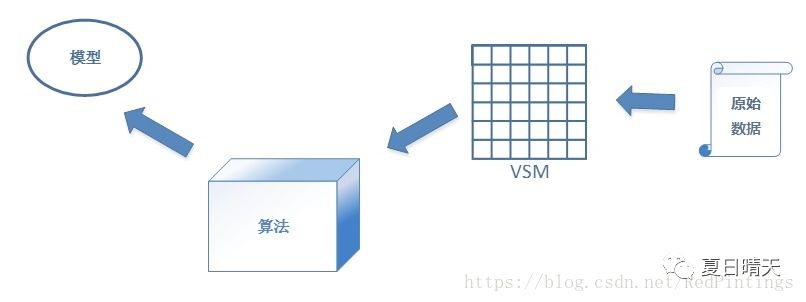
VSM（向量空间模型）建模示意图

--------------------- 

来源：CSDN 

原文：https://blog.csdn.net/lanchunhui/article/details/53302917 

版权声明：本文为博主原创文章，转载请附上博文链接！

分享学习资料：

李航的《统计学习方法》

A Tour of The Top 10 Algorithms for Machine Learning Newbies

（机器学习初学者必须知道的十大算法）

Algorithms Jeff Erickson

希望小李同学有空学习哦

后续

机器学习一定要知道的一下概率论和信息论的基础知识

1、概率论

2、信息论

不知不觉已经有点收不住了，这是要写很多门课程的前导课的节奏啦