强化学习总结 03-动态规划

Posted 2021-04-18 Python与算法之路

↑ 订阅我们，免费获取海量Python学习资源

概述

之前讲到，马尔可夫决策过程的直接解法时间复杂度极高，因此强化学习方法的解法采用迭代式解法，迭代方法中最基础方法是动态规划方法。

之前提到解决序列决策问题有两种手段——学习与规划。 当有一个精确的环境模型时，才可以用动态规划去解。 Q learning等方法均由动态规划所推导而来。 动态规划方法利用了贝尔曼期望方程和贝尔曼最优方程。

• 动态：针对序列问题
• 规划：优化，得到策略

能使用动态规划去解决的问题，需具有以下性质：

• 最优子结构： 满足最优性原理，优的解可以被分解成子问题的最优解。
• 交叠式子问题： 子问题的解能够被多次利用

恰好，MDP就满足这两个特性：

• 回顾贝尔曼期望方程，满足递归形式。【当前状态的值函数 = E(当前的奖励+后继状态×衰减系数) 】，可以把问题分解成子问题
• 值函数的解可以重复利用

使用动态规划解决强化学习问题时，要求知道 MDPs 的所有元素。这是因为强化学习问题中最重要的两个过程，策略评价和策略优化，需要满足：

• 对于 评价的过程：
• 输入： MDP 和策略
• 输出: 值函数
• 对于 优化的过程
• 最优值函数
• 最优策略
• 输入: MDP
• 输出：

---

策略评价

问题描述

问题: 给定一个策略 π，求对应的值函数 （或者 ）。

对于动态规划问题，v 函数和 q 函数是可以相互推导的。

解决方法

1. 直接解：

• 可以直接求得精确解（上一篇文章中）
• 时间复杂度太高

2. 迭代解（√）： -> -> · · · ->

• 利用贝尔曼期望方程迭代求解
• 可以收敛到

利用贝尔曼方程进行迭代式策略评价

贝尔曼方程告诉我们，通过后继状态 的值函数，更新当前状态 的值函数

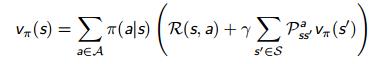
• 表示策略

因此可以得到，

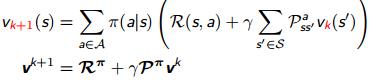
• 注意： 这里的 k 表示第 k 次迭代

从 一直迭代求到最后（能够收敛），可以得到最终的

同步备份下的迭代式策略评价算法

关键词：

• 备份（backup）： 需要用到 。用 更新当前状态状态s的值函数，称为备份状态s。
• 同步（synchronous）： 每一次更新，更新所有的状态。
• 策略评价
• 迭代式

同步备份下的迭代式策略评价算法

为加深理解，引入以下例子：

策略评价例子

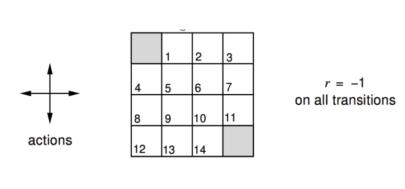
• 假设
• 14个普通状态，2个终止状态
• 走出边界的动作会导致状态不变
• 在走到终止状态前，任何动作都会导致-1的奖励
• 给定一个随机策略

---

策略提升

如何改进策略？

策略提升就是为了改进策略，强化学习的目的就是为了获得最优的策略。

给定一个策略

• 评价策略：求策略对应的值函数
• 策略提升（改进策略）：求得值函数 后，根据贪婪的动作改进策略

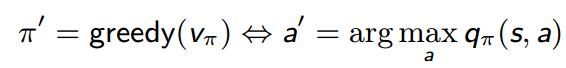
在每个状态下，都选择能使q函数最大的动作。

• ，即 新的策略优于之前的策略
• 使得更新后的策略不差于之前的策略的过程称为 策略提升
• 贪婪动作只是策略提升一种方式

策略提升例子

（接上策略评价例子）

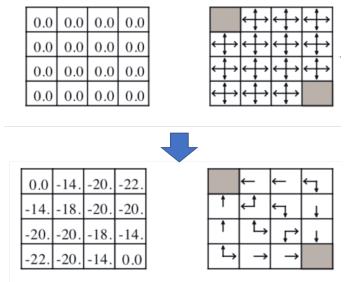
• 通过策略评价和贪婪动作，策略从随机策略变成了最优策略
• 上述的策略比较幸运，策略提升一次就到达了最优
• 一般情况下，可能需要多次迭代（策略评价 + 策略提升）才能到达

策略提升定理

对于两个确定性策略 和 ，如果满足 ，那么可以得到

其中， 表示在当前状态s下，通过策略 选择第一个动作，之后通过策略 进行动作选择，得到的期望回报值。

---

策略迭代

什么是策略迭代？

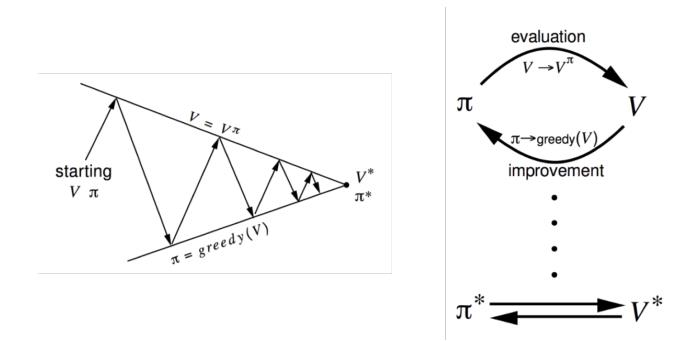
通过不断交替进行策略评价和策略提升，使策略收敛到最优的过程，称为策略迭代。

• 策略评价: 求 。使用方法：迭代式策略评价
• 策略提升: 提升策略 。使用方法: 贪婪策略提升

收敛证明

策略提升停止时，当前策略 达到最优策略 ：

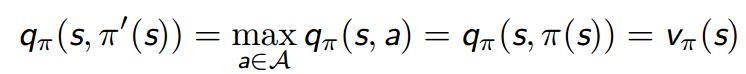
此时，满足贝尔曼最优方程：

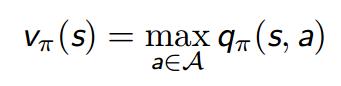
策略迭代算法

策略迭代分为两部分：策略评价和策略提升。 当前的策略评价方法，选用的是迭代式策略评价方法，即通过不断进行迭代，计算出当前策略 的v函数。

利用迭代式策略评价的策略迭代算法为：

一般而言，策略评价需要一直进行迭代求解 。但是策略评价不一定要收敛到 ，才能进行策略提升，可以引入提前停止的规则

• 例如：值函数更新的 ∆ 足够小则停止
• 例如：限定迭代式策略评价只迭代 k 次。（当 时，是值迭代）

策略迭代的进一步思考

• 策略迭代分为两个步骤—— 策略评价和 策略提升
• 一般策略评价需要迭代式求解。因此这里存在 两个循环（ 策略迭代和 策略评价的迭代）
• 策略评价一定要收敛到 ，才能进行策略提升吗？
• 我们是不是可以引入提前停止的规则？
• 例如: 值函数更新的 ∆ 足够小则停止
• 例如：限定迭代式策略评价只迭代 k 次
• 策略评价只迭代一次，就策略提升？（k=1） 值迭代

广义的策略迭代

上述策略迭代方法中，指定了

• 策略评价： 选用 迭代式方法
• 策略提升： 选用 贪婪动作方法

几乎所有的强化学习算法都可以用广义策略迭代（Generalised Policy Iteration, GPI）来描述，GPI不限定两者的方法

• 策略评价： 任何策略评价方法
• 策略提升： 任何策略提升方法（其他的还有：用一定的概率选择原策略，一定的概率选择贪婪策略）

在策略评价中，值函数v只有符合当前策略的情况下才稳定（稳定即迭代后的值函数不变。如果值函数不符合当前策略，就一定能通过迭代进行改变）

策略提升中，策略只有在当前的值函数下，是贪婪的，才稳定。

因此，稳定状态下，分别收敛到最优的 , 。

---

值迭代

强化学习的最优性原理

任何最优的策略都能被分解成两部分

• 最优的初始动作
• 从后继状态 开始沿着最优策略继续进行

一个策略 能够实现从 开始的最优值函数， ，当且仅当 对于任何从状态 开始的后继状态 ， 能实现从状态 开始的最优值函数

值迭代

根据最优性原理，只要知道 （后继状态的最优值函数），即可以知道 （当前状态的最优值函数） 我们只需要选择一步动作即可，值迭代：

该式同时进行了策略评价和策略优化，max操作符表示进行了一次策略提升。

相当于从终止状态的值函数（终止状态的值函数就是它的瞬时奖励）出发，递归地求解之前状态的值函数。

• 同步：每次更新所有状态的值函数

例子

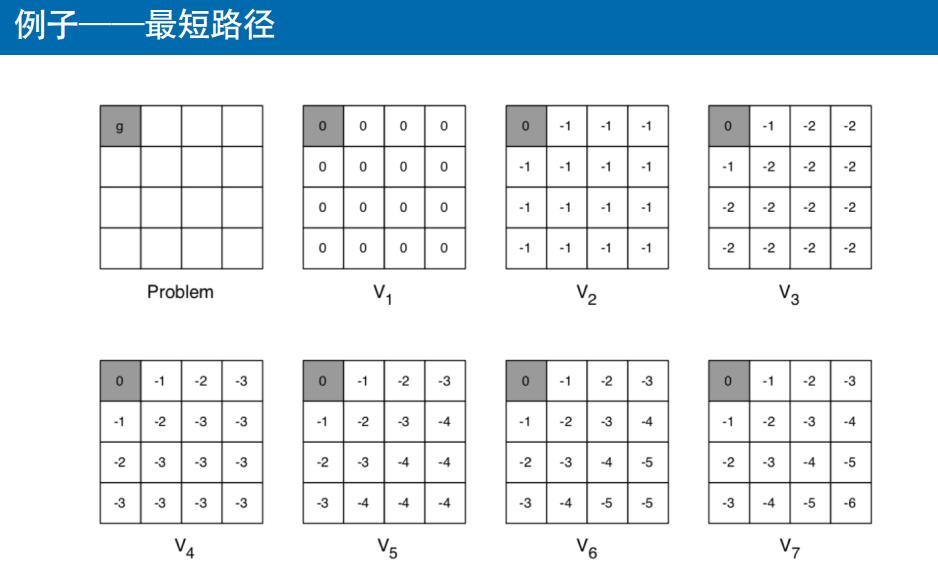
• g 为终止状态，瞬时奖励为 0
• 其他所有状态的瞬时奖励都是 -1
• 7次值迭代就导出最优值函数

值迭代和策略迭代的对比

• 值迭代
• -> -> -> · · · ->
• 没有显式的策略
• 迭代过程中的值函数可能不对应任何策略
• 效率较高（从最后一个状态的最优值函数往前递推即可）
• 贝尔曼最优方程

贝尔曼最优方程Saras 和 Q 学习都是值迭代衍生出来的方法

• 策略迭代
• -> -> -> -> · · · -> ->
• 有显式的策略
• 迭代过程中的值函数对应了某个具体的策略
• 效率较低（一般要两层循环）
• 贝尔曼期望方程 + 贪婪策略提升

---

同步备份下的三种算法总结

• 算法都是基于状态值函数（V 函数）
• 如果一共有动作 个，状态 个, 每次迭代的复杂度为
• 上述算法也可以拓展到状态动作值函数（Q 函数）
• 运用到 Q 函数时，每次迭代的复杂度为 

---