395，动态规划解通配符匹配问题

Posted 2021-04-18 数据结构和算法

If you really like something, you've got to put yourself out there...got to reach out and grab it.

如果你真的喜欢某样东西，你就得置身其中，伸手抓住它。

问题描述

给定一个字符串 (s) 和一个字符模式 (p) ，实现一个支持 '?' 和 '*' 的通配符匹配。

'?' 可以匹配任何单个字符。

'*' 可以匹配任意字符串（包括空字符串）。

两个字符串完全匹配才算匹配成功。

说明:

• s 可能为空，且只包含从 a-z 的小写字母。
  

• p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

示例 1:

输入:

s = "aa"

p = "a"

输出: false

解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

输入:

s = "aa"

p = "*"

输出: true

解释: '*' 可以匹配任意字符串。

示例 3:

输入:

s = "cb"

p = "?a"

输出: false

解释: '?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

示例 4:

输入:

s = "adceb"

p = "*a*b"

输出: true

解释: 第一个 '*' 可以匹配空字符串, 第二个 '*' 可以匹配字符串 "dce".

示例 5:

输入:

s = "acdcb"

p = "a*c?b"

输出: false

问题分析

通配符匹配，如果p的某个位置是字母，那么他只能和s的字母匹配，如果p的某个位置是“?”字符，那么他可以匹配s的任何字母，如果p的某个位置是“*”字符，那么他可以匹配s的任意多个字母。

1，状态定义

dp[i][j]表示s的前i个字符和p的前j个字符是否匹配。我们最后只需要返回

dp[s.length][p.length]即可

2，状态转移

这里分两种情况，一种是p的第j个字符不是*，一个是p的第j个字符是*。

• p的第j个字符不是*
  

  if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1)== '?') 

          dp[i][j] = dp[i - 1][j - 1];

• p的第j个字符是*

  dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
  

第一种

第一种情况比较容易理解，我们可以根据下面的图来看下

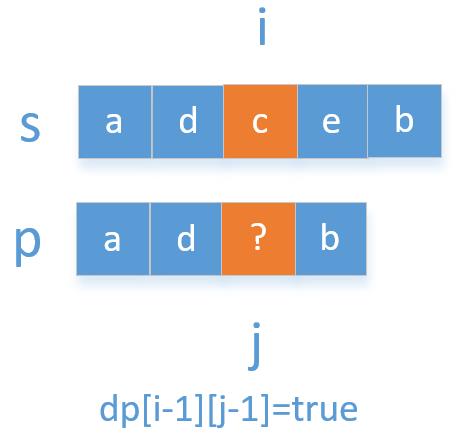
比如上面的s和p的第3个字符匹配成功（要么这两个字符相等，要么p的第3个字符是“?”），我们要看他们前一个字符是否也匹配成功，所以dp[i][j]=dp[i-1][j-1]。

第二种

第二种情况就是p的第j个字符是*，这个*可以匹配0个，也可以匹配多个。

1，如果要匹配0个，也就是判断p的前j-1个字符和s的前i个字符是否匹配，因为匹配0个的话，也就相当于p的第j个字符是空的，所以

dp[i][j]=dp[i][j-1]

2，如果要匹配1个，只需要判断s的前i-1个和p的前j-1个是否匹配，也可以理解为p的第j个和s的第i个同时消失，只需要前面的匹配即可。

dp[i][j]=dp[i-1][j-1]

3，如果要匹配2个的话，只需要判断s的前i-2个和p的前j-1个是否匹配，也可以理解为p的第j个和s的第i和第i-1个同时消失（因为p的*匹配两个，相当于把这两个抵消了，我们只需要判断前面的），只需要前面的匹配即可。

dp[i][j]=dp[i-2][j-1]

4，如果要匹配n个的话，只需要判断s的前i-n个和p的前j-1个是否匹配即可

dp[i][j]=dp[i-n][j-1]

那要这样写下去估计永远写不完了，我们再仔细观察一下。假如p的*要匹配s的n个字符，也就是下面这样

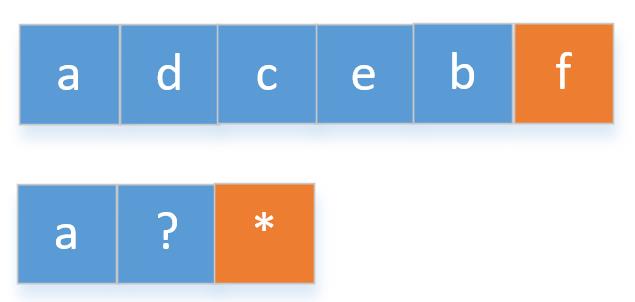
如果要判断p的字符*和s的字符f匹配的话，我们只需要判断p的字符*和s的字符b是否匹配即可。如果要判断这一步我们只需要p的字符*和s的字符e是否匹配即可……，所以我们可以把上面的4个公式简写成一个

dp[i][j]=dp[i-1][j]

综上我们把这题的递推公式找出来了，就是

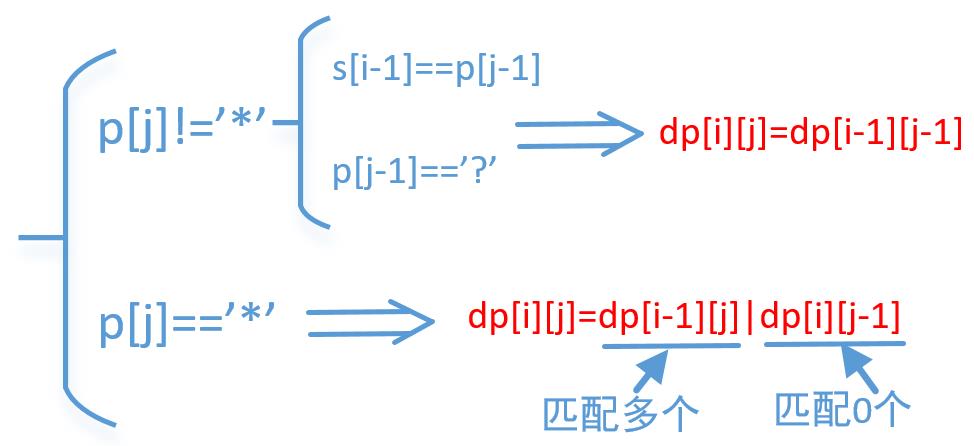
3，边界条件

边界条件很容易发现，如果s和p都为空，我们默认是可以匹配的。否则p最前面有*也是可以匹配的，因为*可以匹配空串。所以边界条件是

boolean[][] dp = new boolean[slen + 1][plen + 1];dp[0][0] = true;for (int j = 1; j <= plen && dp[0][j - 1]; j++) dp[0][j] = p.charAt(j - 1) == '*';

最终代码

通过上面的分析我们来看下最终的完整代码

 1public static boolean isMatch(String s, String p) {
 2    //如果s不为空，p为空，是匹配不成功的，直接返回false
 3    if (s.length() != 0 && p.length() == 0)
 4        return false;
 5
 6    int slen = s.length(), plen = p.length();
 7    boolean[][] dp = new boolean[slen + 1][plen + 1];
 8    dp[0][0] = true;
 9    //边界条件的初始化
10    for (int j = 1; j <= plen && dp[0][j - 1]; j++)
11        dp[0][j] = p.charAt(j - 1) == '*';
12
13    for (int i = 1; i <= slen; i++) {
14        for (int j = 1; j <= plen; j++) {
15            char si = s.charAt(i - 1), pj = p.charAt(j - 1);
16            //下面是动态规划的状态转移方程
17            if (si == pj || pj == '?') {
18                dp[i][j] = dp[i - 1][j - 1];
19            } else if (pj == '*') {
20                dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
21            }
22        }
23    }
24    return dp[slen][plen];
25}
26

代码优化

如果看过之前讲的，我们发现上面的代码和第370题的最长公共子序列的代码有很类似的地方，所以我们也可以参照第370题的代码来优化一下，把上面的二维数组改为一维的，来看下代码

 1public static boolean isMatch(String s, String p) {
 2    //如果s不为空，p为空，是匹配不成功的，直接返回false
 3    if (s.length() != 0 && p.length() == 0)
 4        return false;
 5    int slen = s.length(), plen = p.length();
 6    boolean[] dp = new boolean[plen + 1];
 7    dp[0] = true;
 8    //边界条件的初始化
 9    for (int j = 1; j <= plen && dp[j - 1]; j++)
10        dp[j] = p.charAt(j - 1) == '*';
11
12    for (int i = 1; i <= slen; i++) {
13        //这里的last我们可以认为是上面代码没优化之前的
14        //dp[i - 1][j - 1]
15        boolean last = false;
16        if (i == 1)
17            last = true;
18        for (int j = 1; j <= plen; j++) {
19            //dp[j]使用之后值会被覆盖，所以我们这里在
20            //使用前把它先保留下来
21            boolean temp = dp[j];
22            char si = s.charAt(i - 1), pj = p.charAt(j - 1);
23            //下面是动态规划的状态转移方程
24            if (si == pj || pj == '?') {
25                dp[j] = last;
26            } else if (pj == '*') {
27                dp[j] = dp[j] || dp[j - 1];
28            } else {
29                dp[j] = false;
30            }
31            last = temp;
32        }
33    }
34    return dp[plen];
35}

总结

动态规划基本上都这同一套路，先定义状态表达式，在找转移方程，最后是边界条件。这题可能有一点难度的是当p的第j个字符是*的时候状态方程该怎么写。其实也很好理解，因为*可以匹配0个或多个字符。当匹配0个的时候，也就是相当于判断p的前j-1个字符和s的前i个字符是否匹配。当匹配多个的时候，*可以把s中的多个字符同时消掉，我们先移除掉s中的一个看是否匹配，如果不匹配我们再移除2个……，所以这样很容易找出状态转移方程。

●

●

●

●

长按上图，识别图中二维码之后即可关注。

如果喜欢这篇文章就点个"赞"吧