数学建模与MATLAB——动态规划
Posted Asoul水云天课堂
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学建模与MATLAB——动态规划相关的知识,希望对你有一定的参考价值。
 点击上方“蓝字”,发现更多精彩。
点击上方“蓝字”,发现更多精彩。

什么是动态规划
1、动态规划的定义
2、动态规划的特性
动态规划问题
1、问题示例
(1)最短路径问题
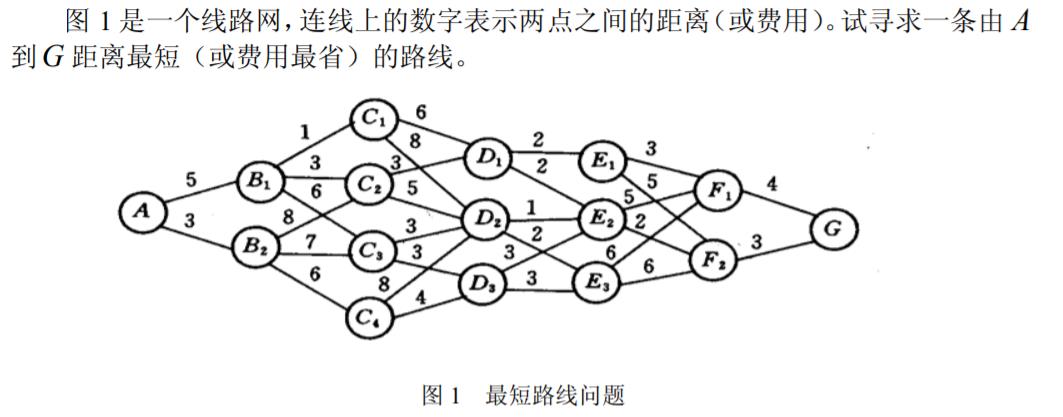
(2)生产计算问题

(3)背包问题

2、动态规划解决问题一般思路
一个动态规划模型主要包含以下要素:
阶段、状态、决策、策略、状态转移方程、指标函数和最优值函数、最优策略和最优轨线、递归方程。
动态规划的解题思路是把多阶段问题进行变换,变换之后为一系列相互联系的单阶段问题,再逐个解决各阶段问题,从而解决整个问题。
一问题示例种最短路径为例,从A到B可以分为一个阶段考虑,从B到C可以分为一个阶段考虑,最后即可考虑到。
3、动态规划与静态规划的异同
动态规划问题解决示例
以问题示例三种背包问题为例(问题求解参考网络博客,参考文献详见文末)
假设五种金银物品以a,b,c,d,e的顺序排放好,那我们可以以金银物品的顺序作为系统的阶段,即第一个物品
(a)作为第一阶段、第二个物品;
(b)作为第二阶段、第三个物品;
(c)作为第三阶段段、… ,那么这个题就划分为了5个阶段了。那系统的状态x(k)为背包当前重量,则
状态转移方程为 x(k+1) = x(k) + u(k);
阶段指标为 v(x(k), u(k)) = x(k);
总目标函数f(x(k))为从第k段的状态x(k)出发到过程终结的背包所装下的金银总价值最大,即
f(x(k)) = max(v(x(k), u(k)) + f(x(k+1)))。
符号说明:
| 符号 | 意义 |
| x(k) | 第k阶段的状态,状态就是第k阶段时的背包的重量 |
| u(k) | 第k阶段的决策,决策取1表示将第k个物品放入背包,取0则相反 |
| v(x(k), u(k)) | 第k阶段的阶段指标,也就是决策的取到的第k个物品的价值 |
| f(x(k)) | 总目标函数,即背包承重的范围内要能装走最大价值的金银财宝 |
代码展示:
%此代码来源于网络博客
clear,clc
a = [1 2 3 4 5; % 第一行是金银类型,用来表示系统的状态
2 2 6 5 4; % 第二行是金银重量
6 3 5 4 6]; % 第三行是金银价值
b = perms(a(1, :));
v = [];
for i = 1:size(a,2)-1
c = b;
id1 = find(c <= i);
id2 = find(c > i);
c(id1) = 0;
c(id2) = 1;
c = unique(c,'rows');
v = [v; c]; % 用0、1变量表示第k状态的决策
end
v = [ones(1,5); v; zeros(1,5)]; % 所有阶段的所有状态都存放在v中
F = [];
for i = 1:size(v,1)
if (a(2,:) * v(i,:)') <= 10 % 约束条件(背包的承重范围内)
f = (a(3,:) * v(i,:)'); % 阶段指标
F = [F, f]; % 指标函数
end
end
best_value = max(F) % 指标函数最优值
计算结果:
best_value =15
下面是一些写的比较好的博客,希望对大家有用

知乎对于动态规划的博客:https://www.zhihu.com/question/23995189
彻底学会动态规划:https://blog.csdn.net/baidu_28312631/article/details/47418773
动态规划解题框架:https://blog.csdn.net/ryontang/article/details/107745991
动态规划套路详解:https://juejin.im/post/6844903916908331015
动态规划从菜鸟到老鸟:https://blog.csdn.net/u013309870/article/details/75193592

文中部分示例来源于网络,只用于学习交流!由于能力有限,部分地方难免出现错误,请大家批评指正!
953314432

以上是关于数学建模与MATLAB——动态规划的主要内容,如果未能解决你的问题,请参考以下文章
MATLAB应用实战系列(六十)-MATLAB数学建模常用的四大模型