学会背包问题，再也不怕动态规划

Posted 沉风网事

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了学会背包问题，再也不怕动态规划相关的知识，希望对你有一定的参考价值。

问题描述

Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays val[0..n-1] and wt[0..n-1] which represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the maximum value subset of val[] such that sum of the weights of this subset is smaller than or equal to W. You cannot break an item, either pick the complete item, or don’t pick it (0-1 property).

给定n个物品的重量和价值，从中选择物品放在容量为W的背包中(表示选择物品重量不超过W)，使得背包中物品价值之和最高。

背包问题是一个非常典型的考察动态规划应用的题目，对其加上不同的限制和条件，可以衍生出诸多变种，若要全面理解动态规划，就必须对背包问题了如指掌。学习背包问题有利于举一反三，融会贯通，再也不怕动态规划。

问题建模

用程序语言重新定义一下问题。

先看输入：

  1. int Values[n]，表示物品的价值

  2. int Weights[n]，表示物品的重要

  3. int LimitWeight，表示背包容量的限制

再看输出：

  1. int MaxValue，表示背包里的物品最大价值

转化为函数（以C++为例）：

int knapsack(vector<int> Values, vector<int> Weights, int LimitWeight)
{
    int  MaxValue = 0;

    return  MaxValue;
}

问题分析

是否可以应用DP

应用DP应以满足以下三个条件：

  1. 最优子结构

  2. 边界条件

  3. 满足重叠要求的状态转移方程

最优子结构

如果一个问题的最优解包含其子问题的最优解，我们就称此问题具有最优子结构。　　　　　　　　　　　　　　　　　　　　　　

编程中常见最大与最小的问题，一般都是满足最优子结构的这一条件。

本题要求是求背包里物品的最大价值。故初步判断满足条件。

边界条件

边界条件包括开始条件与结束条件。

这个条件可以从下面三个问题来解答：

  1. 用什么来作边界条件？

  2. 边界条件是起点是什么，终点是什么？

  3. 边界是如何从起点到终点？

针对上面问题，结合本题的信息，可以回答如下：

  1. 用背包里的物品重量作为边界

  2. 重量限制起点是1，终点是不超过LimitWeight；物品在数组的位置起点从0开始，终点不超过数组的长度

  3. 从起点开始，逐个加1直到终点

状态转移方程

状态转移方程也就是我们常说的DP公式。这是解决DP问题的关键。

满足重叠要求是指后面的状态可以重复使用前面的生成的状态。

如果不是很简单的直接可以看出来，建议在解题步骤中一步一步分析出来。本题我们会在后面分析给出对应的状态转移方程。

解题步骤

确定采用DP来解决问题，那我们正式进行DP解题的步骤。

1. 定义状态

前面问题分析中提到状态转移方程，状态应当在状态转移方程之前定义。完成状态定义，才能开始定义状态转移方程。

本题的状态是S(w,i,v),其中w表示不能超过最大重量，i表示遍历到第i个物品，v表示对应的最大的价值。

那么如何用数据结构保存状态呢？

使用一个二维数组state[LimitWeight+1][n+1]来表示。

2. 确定递归关系

这里我们采用top-down思考方式。

先看代码，具体如下：

int knapsack(vector<int> Values, vector<int> Weights, int LimitWeight)
{
    int  MaxValue = 0;
    int  itemLen = Weights.size();
    // 处理入口
    MaxValue = knapsackDo(Values, Weights, LimitWeight,itemLen);
    return  MaxValue;
}

int knapsackDo(vector<int> Values, vector<int> Weights, int LimitWeight, int posIndex)
{
    int localMaxValue  = 0;
    int posWeight = Weights[posIndex-1];
    int posValue = Values[posIndex-1];
    if(LimitWeight >=posWeight){
        // 选择当前位置的物品
        int  selectValue = posValue +  knapsackDo(Values, Weights, LimitWeight- posValue, i -1);
        // 跳过当前位置的物品
        int  skipValue  = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
        localMaxValue = MAX(selectValue, skipValue);
    }else {
        // 超过重量限制，跳过
        localMaxValue = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
    }

    return localMaxValue;
}

3. 根据递归关系，得出并检查状态转移方程

当限制重量大于等于当前物品重量时，状态转移方程如下：

knapsackDo(Values, Weights, LimitWeight,posIndex) =
MAX(knapsackDo(Values,Weights, LimitWeight - Weights[posIndex],posIndex -1),
knapsackDo(Values,Weights, LimitWeight,posIndex -1))

当限制重量小于当前物品重量时，状态转移方程如下：

knapsackDo(Values, Weights, LimitWeight,posIndex) =
knapsackDo(Values,Weights, LimitWeight,posIndex -1)

4. 确定递归结束条件

本题中递归结束条件有两个，分别如下：

  1. 限制重量小于等于0（即0 >= LimitWeight ）

  2. 数组index小于0 （即0 > posIndex）

int knapsackDo(vector<int> Values, vector<int> Weights, int LimitWeight, int posIndex)
{
   // 递归结束条件
    if( 0 >= LimitWeight || 0 > posIndex ){
        return 0;
    }
    int localMaxValue  = 0;
    int posWeight = Weights[posIndex-1];
    int posValue = Values[posIndex-1];
    if(LimitWeight >=posWeight){
        // 选择当前位置的物品
        int  selectValue = posValue +  knapsackDo(Values, Weights, LimitWeight- posValue, posIndex -1);
        // 跳过当前位置的物品
        int  skipValue  = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
        localMaxValue = MAX(selectValue, skipValue);
    }else {
        // 超过重量限制，跳过
        localMaxValue = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
    }

    return localMaxValue;
}

5. 完成递归的实现

将代码结合起来如下：

 int knapsack(vector<int> Values, vector<int> Weights, int LimitWeight)
{
    int  MaxValue = 0;
    int  itemLen = Weights.size();
    // 处理入口
    MaxValue = knapsackDo(Values, Weights, LimitWeight,itemLen-1);
    return  MaxValue;
}

int knapsackDo(vector<int> Values, vector<int> Weights, int LimitWeight, int posIndex)
{
    if( 0 >= LimitWeight || 0 > posIndex ){
        return 0;
    }
    int localMaxValue  = 0;
    int posWeight = Weights[posIndex];
    int posValue = Values[posIndex];
    if(LimitWeight >=posWeight){
        // 选择当前位置的物品
        int  selectValue = posValue +  knapsackDo(Values, Weights, LimitWeight- posValue, posIndex -1);
        // 跳过当前位置的物品
        int  skipValue  = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
        localMaxValue = MAX(selectValue, skipValue);
    }else {
        // 超过重量限制，跳过
        localMaxValue = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
    }

    return localMaxValue;
}

6. 添加缓存保存子问题结果优化递归方案

缓存对象是什么？状态。根据状态定义，添加如下代码：

int knapsack(vector<int> Values, vector<int> Weights, int LimitWeight)
{
    int  MaxValue = 0;
    int  itemLen = Weights.size();
    // 定义与实始化状态 
    static  vector<vector<int>> stateDP(LimitWeight+1, vector<init>(itemLen+1));
    // 处理入口
    MaxValue = knapsackDo(Values, Weights, LimitWeight, itemLen - 1);
    return  MaxValue;
}

什么时候添加缓存与什么时候使用缓存呢？

具体代码如下：

int knapsackDo(vector<int> Values, vector<int> Weights, int LimitWeight, int posIndex)
{
    if( 0 >= LimitWeight || 0 > posIndex ){
        return 0;
    }

    int localMaxValue  = 0;
    int posWeight = Weights[posIndex];
    int posValue = Values[posIndex];
    
    if(LimitWeight >=posWeight){
        // 选择当前位置的物品
        if(0 != stateDP[LimitWeight][posIndex+1]){
            // 使用缓存
            int  selectValue = stateDP[LimitWeight][posIndex+1];
        }else {
            int  selectValue = posValue +  knapsackDo(Values, Weights, LimitWeight- posValue, i -1);
            // 添加缓存
            stateDP[LimitWeight][posIndex+1]  = selectValue；
        }
        // 跳过当前位置的物品
        int  skipValue  = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
        localMaxValue = MAX(selectValue, skipValue);
    }else {
        // 超过重量限制，不能选择
        localMaxValue = knapsackDo(Values, Weights, LimitWeight, posIndex -1);
    }

    return localMaxValue;
}

注意：根据代码执行顺序，只需要添加上面一处添加缓存处理代码即可。

7. 将递归转化为迭代

上面一直采用的是top-down来解决DP问题。这一步我们要尝试将递归转化为迭代。

递归的情况下状态转移方程是函数的方程。在迭代的情况，状态转移方程是状态变量的方程，具体如下：

当限制重量大于等于当前物品重量时，状态转移方程如下：

stateDP[LimitWeight][posIndex] =
MAX(stateDP(Values,Weights, LimitWeight - Weights[posIndex], posIndex -1),
stateDP(Values,Weights, LimitWeight,posIndex -1))

当限制重量小于当前物品重量时，状态转移方程如下：

stateDP[LimitWeight][posIndex] = stateDP[LimitWeight][posIndex -1]

代码如下：

 int knapsack(vector<int> Values, vector<int> Weights, int LimitWeight)
{
    int  MaxValue = 0;
    int  itemLen = Weights.size();
    // 定义与实始化DP状态 
    vector<vector<int>> stateDP(LimitWeight+1, vector<int>(itemLen+1));

    // 限定重量从1开始
    for(int w  = 1;  w  <= LimitWeight; w++){
        // 在限定重量为w的情况下，遍历数组获取最大值
        for(int posIndex = 1; posIndex <= itemLen;  posIndex++){
            int  selectValue = 0;
            int  skipValue = stateDP[w][posIndex -1];
            int  posWeight = Weights[posIndex -1];
            int  posValue = Values[posIndex -1];
            if (w  >=  posWeight)  {
                 selectValue = posValue + stateDP[w - posWeight][posIndex -1];
            }
            stateDP[w][posIndex]  = max(skipValue, selectValue);
        }
    }
    // 从状态中取出最大值
    MaxValue = stateDP[LimitWeight][itemLen];
    return  MaxValue;
}

为了方便理解上面的代码，我们进行一个实例分析：

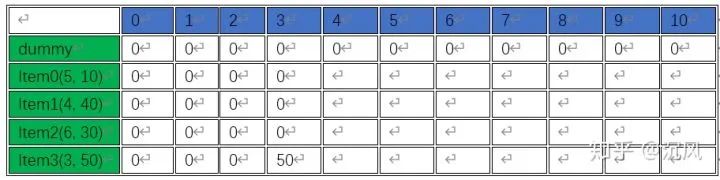
假定有4个物品，其价值分别为10, 40, 30, 50，对应重量分别为5, 4, 6, 3，限定总重量不超过10。下面我们观察stateDP的变化过程。

首先看初始化的stateDP状态：


学会背包问题，再也不怕动态规划


根据初始化的stateDP状态和状态转移方程，整个stateDP状态构建一列一列进行即可，过程与结果如下：


学会背包问题，再也不怕动态规划




8. 测试

#include <iostream>
#include <vector>
#include <algorithm>    // std::max
#include <iomanip>
using namespace std;


int knapsack(vector<int> Values, vector<int> Weights, int LimitWeight)
{
    int  MaxValue = 0;
    int  itemLen = Weights.size();
    // 定义与实始化DP状态 
    vector<vector<int>> stateDP(LimitWeight+1, vector<int>(itemLen+1));

    // 限定重量从1开始
    for(int w  = 1;  w  <= LimitWeight; w++){
        // 在限定重量为w的情况下，遍历数组获取最大值
        for(int posIndex = 1; posIndex <= itemLen;  posIndex++){
            int  selectValue = 0;
            int  skipValue = stateDP[w][posIndex -1];
            int  posWeight = Weights[posIndex -1];
            int  posValue = Values[posIndex -1];
            if (w  >=  posWeight)  {
                 selectValue = posValue + stateDP[w - posWeight][posIndex -1];
            }
            stateDP[w][posIndex]  = max(skipValue, selectValue);
        }
    }
    // 从状态中取出最大值
    MaxValue = stateDP[LimitWeight][itemLen];
    // 打印状态表
    cout<<"print stateDP:"<<endl;
    for(int  i = 0; i  <= itemLen; i++){
        for(int j  = 0; j  <= LimitWeight; j++){
            cout<<setw(2)<<stateDP[j][i]<<" ";
        }
        cout <<endl;
    }
    return  MaxValue;
}

int main(){
    vector<int> Values{10, 40, 30, 50};
    vector<int> Weights{5, 4, 6, 3};
    int LimitWeight = 10;
    int maxValues = knapsack(Values, Weights, LimitWeight);
    cout<<"maxValues:"<<maxValues;
}

运行结果如下：

print stateDP:

 0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0 10 10 10 10 10 10
 0  0  0  0 40 40 40 40 40 50 50
 0  0  0  0 40 40 40 40 40 50 70
 0  0  0 50 50 50 50 90 90 90 90
maxValues:90

推荐是在leetcode测试，由于leetcode上没有这道题，所以就简单测试一下。

测试代码参考链接。

总结

掌握使用DP解决问题三个条件：

  1. 最优子结构

  2. 边界条件

  3. 满足重叠要求的状态转移方程

使用DP解决问题采用以下步骤：

  1. 定义状态

  2. 确定递归关系

  3. 根据递归关系，得出并检查状态转移方程

  4. 确定递归结束条件

  5. 完成递归的实现

  6. 添加缓存保存子问题结果优化递归方案

  7. 将递归转化为迭代

对上面的步骤总结如下：

根据问题的目标采用Top-down方式弄清问题的本质（状态转移方程），然后采用Bottom-up方式实现代码。

Ps：关于DP还有很多内容可以写（如背包问题的扩展及类似leetcode题目），以后有机会再补充一些。

欢迎关注

欢迎关注微信公众帐号：沉风网事(savewind)


以上是关于学会背包问题，再也不怕动态规划的主要内容，如果未能解决你的问题，请参考以下文章

有了这些套路，面试再也不怕遇到动态规划！

Thinkphp调用微信扫一扫实例，学会再也不怕客户在微信提的奇葩要求了

Thinkphp调用微信扫一扫实例，学会再也不怕客户在微信提的奇葩要求了

内卷这么严重！学会这些java核心资料，再也不怕行业内卷了

备战蓝桥杯----完全背包问题（动态规划）

动态规划_01背包_完全背包_多重背包_分组背包