算法萌新如何学好动态规划（第一弹）

Posted 2021-04-18 力扣加加

下面开始今天的学习～

动态规划问题一直是大厂面试时最频繁出现的算法题，主要原因在于此类问题灵活度高，思维难度大，没有很明显的套路做法。

也正是因为这个原因，我们打算出一个「动态规划」系列文章来尝试破解面试中所涉及的动态规划问题。而本文就是这个系列的第一篇文章，主要目的是说明动态规划是什么，动态规划问题应该如何思考？

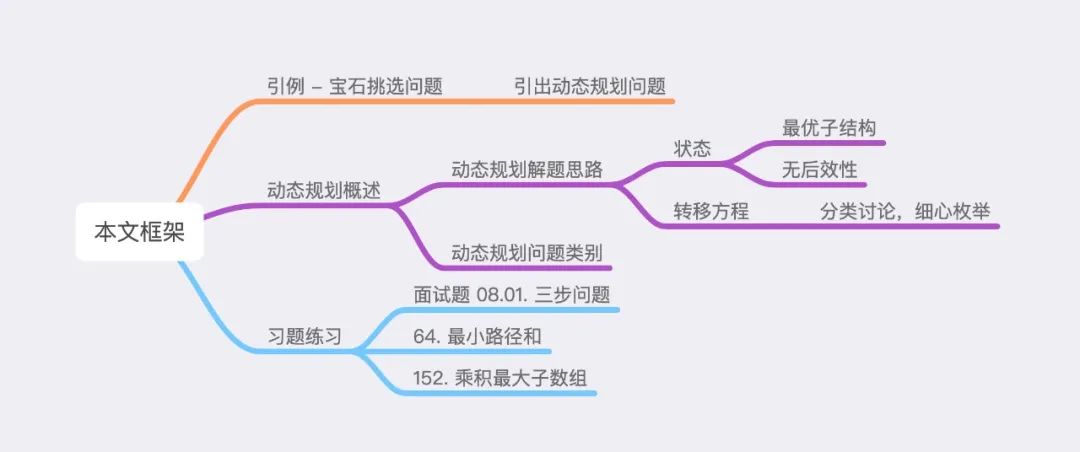
本文一共分成三个部分，具体内容框架如下所示：

宝石挑选

问题引入

小 Q 是一个宝石爱好者。

这一天，小 Q 来到了宝石古董店，店家觉得小 Q 是个宝石行家，于是决定和小 Q 玩一个游戏。

游戏是这样的，一共有 n 块宝石，每块宝石在小 Q 心中都有其对应的价值。注意，由于某些宝石质量过于差劲，因此存在只有店家倒贴钱，小 Q 才愿意带走的宝石，即价值可以为负数。

小 Q 可以免费带走一个连续区间中的宝石，比如区间 [1,3] 或区间 [2,4] 中的宝石。

请问小 Q 能带走的最大价值是多少？

问题分析

首先思考最暴力的解法。

枚举所有区间，暴力累加区间中宝石的价值，最后选一个价值最大的区间。时间复杂度 O(n^3)。

O(n^3) 显然有些无法接受，因此想想有没有办法优化，比如优化掉暴力累加的部分。

优化 1.0

仔细思考不难发现，我们可以枚举区间右端点，然后固定右端点，左端点不断向左移动，边移动边累加，就可以将时间复杂度优化到 O(n^2)。

例如我们固定右端点是 3，那么左端点就从 3 移动到 1，边移动边累加答案，就可以在移动过程中计算出区间 [3,3]、[2,3]、[1,3] 的答案了。因此枚举所有区间右端点，即可在 O(n^2) 时间复杂度内找到答案。

但是 O(n^2) 时间还是有些过高了，因此思考有没有办法继续优化呢？

优化 2.0

观察 O(n^2) 的解法，不难发现我们用了 O(n) 的时间复杂度才求出了固定某个点为区间右端点时，区间最大价值和。

例如固定了 n 为区间右端点后，我们通过从 n 到 1 枚举左端点，才求出了以 n 为区间右端点时的区间最大价值和，即 O(n) 的时间复杂度。

那么继续思考，「以 n 为区间右端点的区间最大和」，与「以 n - 1 为区间右端点的区间最大和」，这两者是否有关联呢？

为了描述方便，接下来我们用 f[i] 来代替「以 i 为区间右端点的区间最大和」，用  a[i] 来代替第 i 块宝石的价值。

不难发现，如果 f[n - 1] 为正数，则 f[n] 一定等于 f[n - 1] + a[n]；如果 f[n - 1] 为负数，则 f[n] 一定等于 a[n]。因此我们可以推导出如下转移方程：

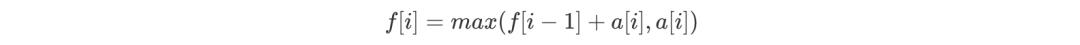
根据上述转移方程，我们可以在 O(n) 时间复杂度内求出最大的 f[i]，即将此题时间复杂度优化到 O(n)，而这个优化的过程就是「动态规划」的过程。

在上述推导过程中，一共分为两步：

1. 将整个问题划分为一个个子问题，并令 f[i] 为第 i 个子问题的答案

2. 思考大规模的子问题如何从小规模的子问题推导而来，即如何由 f[i - 1] 推出 f[i]

这两个步骤便是「动态规划」解题思路的核心所在，即确定动态规划时的「状态」与「转移方程」。

动态规划概述

动态规划（Dynamic Programming），因此常用 DP 指代动态规划。本块内容我们主要讲解「动态规划解题思路」与「动态规划问题类别」。

动态规划解题思路

动态规划主要分为两个核心部分，一是确定「DP 状态」，二是确定「DP 转移方程」。

DP 状态

「DP 状态」的确定主要有两大原则：

1. 最优子结构
2. 无后效性

最优子结构

我们仍以「宝石挑选」例题来讲解这两大原则，首先是「最优子结构」。

什么是「最优子结构」？将原有问题化分为一个个子问题，即为子结构。而对于每一个子问题，其最优值均由「更小规模的子问题的最优值」推导而来，即为最优子结构。

因此「DP 状态」设置之前，需要将原有问题划分为一个个子问题，且需要确保子问题的最优值由「更小规模子问题的最优值」推出，此时子问题的最优值即为「DP 状态」的定义。

例如在「宝石挑选」例题中，原有问题是「最大连续区间和」，子问题是「以 i 为右端点的连续区间和」。并且「以 i 为右端点的最大连续区间和」由「以 i - 1 为右端点的最大连续区间和」推出，此时后者即为更小规模的子问题，因此满足「最优子结构」原则。

由此我们才定义 DP 状态 f[i] 表示子问题的最优值，即「以 i 为右端点的最大连续区间和」。

无后效性

而对于「无后效性」，顾名思义，就是我们只关心子问题的最优值，不关心子问题的最优值是怎么得到的。

仍以「宝石挑选」例题为例，我们令 DP 状态 f[i] 表示「以 i 为右端点的最大连续区间和」，我们只关心「以 i 为右端点的区间」这个子问题的最优值，并不关心这个子问题的最优值是从哪个其它子问题转移而来。

即无论 f[i] 所表示区间的左端点是什么，都不会影响后续 f[i + 1] 的取值。影响 f[i + 1] 取值的只有 f[i] 的数值大小。

那怎样的状态定义算「有后效性」呢？

我们对「宝石挑选」例题增加一个限制，即小 Q 只能挑选长度 <= k 的连续区间。此时若我们定义 f[i] 表示「以 i 为右端点的长度 <= k 的最大连续区间和」，则 f[i + 1] 的取值不仅取决于 f[i] 的数值，还取决于 f[i] 是如何得到的。

因为如果 f[i] 取得最优值时区间长度 = k，则 f[i + 1] 不能从 f[i]  转移得到，即 f[i] 的状态定义有后效性。

最后概括一下，「最优子结构」就是「DP 状态最优值由更小规模的 DP 状态最优值推出」，此处 DP 状态即为子问题。而「无后效性」就是「无论 DP 状态是如何得到的，都不会影响后续 DP 状态的取值」。

DP 转移方程

有了「DP 状态」之后，我们只需要用「分类讨论」的思想来枚举所有小状态向大状态转移的可能性即可推出「DP 转移方程」。

我们继续以「宝石挑选」问题为例。

在我们定义「DP 状态」f[i] 之后，我们考虑状态 f[i] 如何从 f[1] ~ f[i - 1] 这些更小规模的状态转移而来。

仔细思考可以发现，由于 f[i] 表示的是连续区间的和，因此其取值只与 f[i - 1] 有关，与 f[1] ~ f[i - 2] 均无关。

我们再进一步思考，f[i] 取值只有两种情况，一是向左延伸，包含 f[i - 1]，二是不向左延伸，仅包含 a[i]，由此我们可以得到下述「DP 转移方程」：

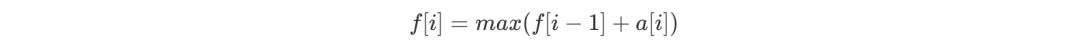
注意，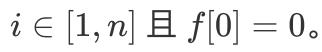

动态规划问题类别

讲述完 DP 问题的解题思路后，我们来大致列举一下 DP 问题的类别。

DP 问题主要分为两大类，第一大类是 DP 类型，第二大类是 DP 优化方法。

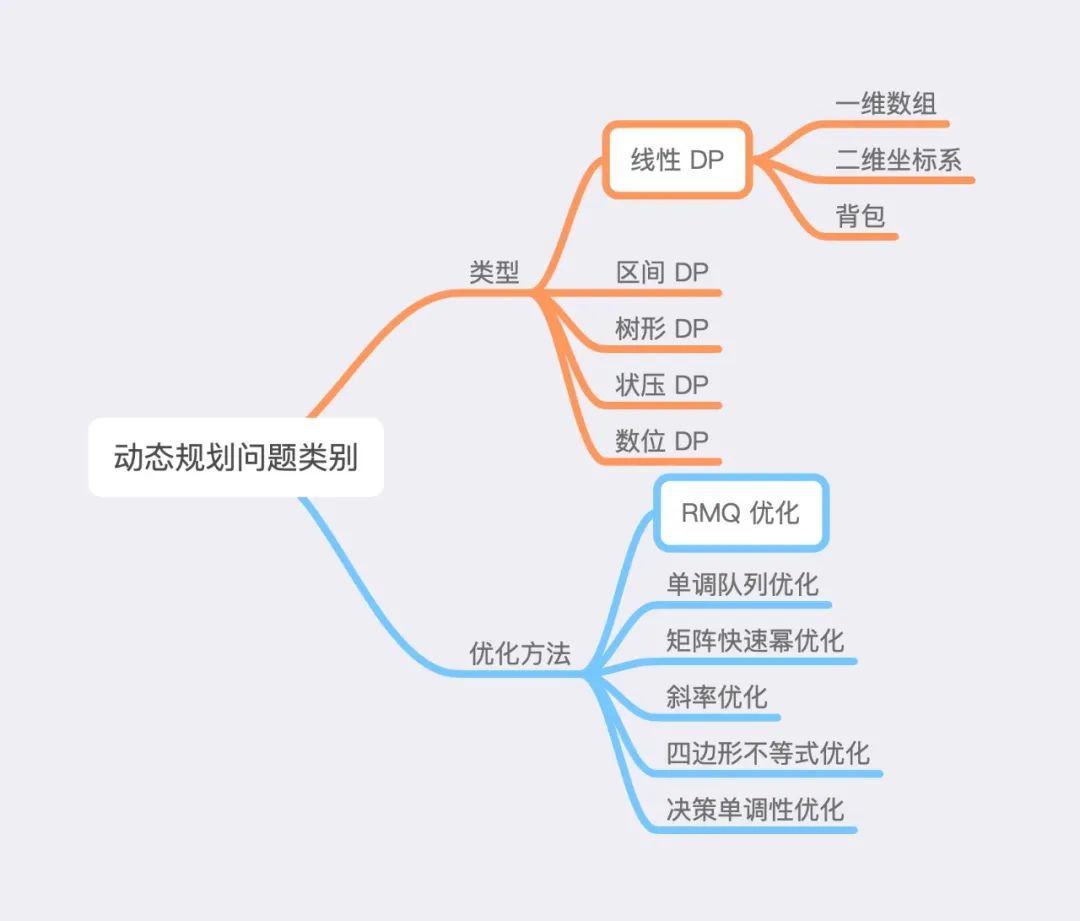
其中在 DP 类型部分，面试中最常考察的就是「线性 DP」，而在优化方法部分，最常见的是「RMQ 优化」，即使用线段树或其它数据结构查询区间最小值，来优化 DP 的转移过程。

习题练习

接下来我们以三道习题为例，来强化一下确定「DP 状态」和「DP 转移方程」的 DP 问题求解思路。

面试题 08.01. 三步问题

题目描述

三步问题。有个小孩正在上楼梯，楼梯有 n 阶台阶，小孩一次可以上 1 阶、2 阶或 3 阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模 1000000007。

示例 1:

输入：n = 3 输出：4说明: 有四种走法

示例 2:

输入：n = 5输出：13

数据范围

n 范围在 [1, 1000000] 之间

解题思路

DP 问题思路主要就是确定「DP 状态」与「DP 转移方程」，因此我们首先考虑「DP 状态」。

「DP 状态」的确定有两大原则，一是「最优子结构」，二是「无后效性」，简要概括就是将原问题划分为多个子问题，且「大规模子问题最优值」仅与「小规模子问题最优值」有关，与「小规模子问题最优值」是如何得到的无关。

此题需要求出爬 n 阶楼梯的总方案数，因此很容易想到子问题是爬 i 阶楼梯的总方案数。接下来再进一步验证该状态是否符合「最优子结构」与「无后效性」两大原则。

令 f[i] 表示爬 i 阶楼梯的总方案数，原问题被划分为了多个求最优值的子问题，继续思考，不难发现小孩爬楼梯只有三种选项，一次上 1、2、3 阶，因此 f[i] 的值仅由 f[i - 1]、f[i - 2]、f[i - 3] 的值决定，因此符合「最优子结构」原则。

再进一步思考，f[i] 的取值与 f[i - 1]、f[i - 2]、f[i - 3] 的数值是如何得到的无关，因此符合「无后效性」原则。

确定完「DP 状态」后，我们再来确定「DP 转移方程」。

由于小孩只有三种爬楼选项，因此 f[i] 的值仅由 f[i - 3] ～ f[i - 1] 决定。且由于爬楼的最后一步不同，因此 f[i] 的值由 f[i - 3] ～ f[i - 1] 累加得到，即如下所示：

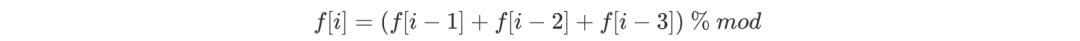
注意，f[1] = 1，且转移时需要注意 f[i - 1]、f[i - 2]、f[i - 3] 不要越界。

C++ 代码实现

class Solution {public: vector<int> f; int mod = 1000000007; int waysToStep(int n) { f.resize(n+1); f[0] = 1; for(int i = 1; i <= n; i++) { f[i] = f[i-1]; if(i >= 2) f[i] = (f[i] + f[i-2]) % mod; if(i >= 3) f[i] = (f[i] + f[i-3]) % mod; } return f[n]; }};

64. 最小路径和

题目描述

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1:

输入:[ [1,3,1], [1,5,1], [4,2,1]]输出: 7解释: 因为路径 1→3→1→1→1 的总和最小。

解题思路

仍然是相同的解题思路，即依次确定「DP 状态」与「DP 转移方程」，且「DP 状态」的确定需要满足「最优子结构」与「无后效性」。

此题需要求出从左上角出发，到达坐标（m,n）的路径数字和最小值。因此不难想到，子问题就是从左上角出发，到达坐标（i,j）的路径数字和最小值。

令 f[i][j] 表示从左上角到坐标（i,j）的路径数字和最小值，原问题即可被划分为多个求最优值的子问题，且由于每次只能向下或向右移动一步，因此 f[i][j] 的取值由 f[i - 1][j] 和 f[i][j - 1] 的值决定，即符合「最优子结构原则」。

进一步验证，可以发现，f[i][j] 的取值与 f[i - 1][j] 和 f[i][j - 1] 所对应的具体路径无关，因此符合「无后效性」。

此处啰嗦一下。如果题目改为每次可以向上、下、左、右移动一步，且不能走重复的格子，则 f[i][j] 的值虽然与 f[i][j - 1]、f[i][j + 1]、f[i - 1][j]、f[i + 1][j] 的值有关，但由于「不能走重复的格子」这一限制，f[i][j - 1] ～ f[i + 1][j] 所对应的具体路径会影响到 f[i][j] 的取值，即不符合「无后效性」。

确定完「DP 状态」后，继续确定「DP 转移方程」。

由于只能向下或向右移动一步，且由于其最后一步不同，因此 f[i][j] 由 f[i - 1][j] 和 f[i][j - 1] 中的最小值转移得到，即如下所示：

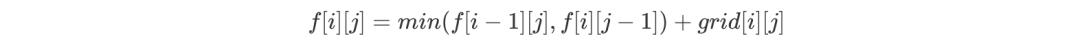
注意，grid[i][j] 表示坐标（i,j）处的数字大小，f[1][1] = grid[1][1] ，转移时需要注意不要越界。

C++ 代码实现

class Solution {public: int minPathSum(vector<vector<int>>& grid) { for(int i = 0; i < grid.size(); i++) for(int j = 0; j < grid[0].size(); j++) { if(i == 0 && j == 0) continue; int tp = 1e9; if(i > 0) tp = min(tp, grid[i-1][j]); if(j > 0) tp = min(tp, grid[i][j-1]); grid[i][j] += tp; } return grid[grid.size()-1][grid[0].size()-1]; }};

152. 乘积最大子数组

题目描述

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例 1:

输入: [2,3,-2,4]输出: 6解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: [-2,0,-1]输出: 0解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

解题思路

继续采用相同的解题思路，即依次确定「DP 状态」与「DP 转移方程」，且「DP 状态」的确定需要满足「最优子结构」与「无后效性」。

此题其实是「宝石挑选」问题的进阶版，即连续区间最大乘积。因此与「宝石挑选」问题的思路一致，令 f[i] 表示以 i 为右端点的连续区间最大乘积，即可将原问题划分为多个求最优值的子问题，但这个状态定义是否符合「最优子结构」原则呢？

我们可以举一个例子来进一步思考。

例如给出 nums = [2,-1,-2]，根据上述 f[i] 的定义，我们可以得到 f = [2,-1,4]。不难发现 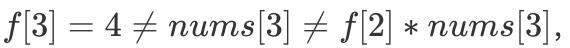f[i] 的值与 f[i - 1] 的值无关，即 DP 状态最优值无法由更小规模的 DP 状态最优值推出，因此不符合「最优子结构」原则。

于是问题来了，怎样的状态定义才符合「最优子结构」呢？

继续思考可以发现，上述状态定义出错的原因主要在于如果 nums[i] 为负数，则 f[i - 1] * nums[i] 只会越乘越小。因此我们需要根据 nums[i] 的正负值进行分类讨论：

由此可以发现，我们需要引入新的「DP 状态」。令 maxn[i] 表示「以 i 为右端点的连续区间最大乘积」，minn[i] 表示「 以 i 为右端点的连续区间最小乘积」。

不难发现 maxn[i]、minn[i] 的取值由 maxn[i - 1] 、minn[i - 1] 的值推导而来，且与其具体的区间大小无关，因此同时满足「最优子结构」与「无后效性」原则。

最后我们再通过「分类讨论」即可确定如下「DP 转移方程」：

if(nums[i] > 0) { maxn[i] = max(nums[i], maxn[i - 1] * nums[i]); minn[i] = min(nums[i], minn[i - 1] * nums[i]);}else { maxn[i] = max(nums[i], minn[i - 1] * nums[i]); minn[i] = min(nums[i], maxn[i - 1] * nums[i]);}

总结一下，此题根据「最优子结构」原则否定了第一种状态定义。 否定之后进一步观察题目性质，得到了新的「DP 状态」，并通过「分类讨论」的方式推出「DP 转移方程」，使得本题得以圆满解决。

C++ 代码实现

class Solution {public: vector<int> maxn, minn; int maxProduct(vector<int>& nums) { int n = nums.size(), ans = nums[0]; maxn.resize(n); minn.resize(n); maxn[0] = minn[0] = nums[0]; for (int i = 1; i < nums.size(); ++i) { if(nums[i] > 0) { maxn[i] = max(nums[i], maxn[i - 1] * nums[i]); minn[i] = min(nums[i], minn[i - 1] * nums[i]); } else { maxn[i] = max(nums[i], minn[i - 1] * nums[i]); minn[i] = min(nums[i], maxn[i - 1] * nums[i]); } ans = max(ans, maxn[i]); } return ans; }};

总结

最后我们来总结一下 DP 问题的解题思路：

• 确定「DP 状态」
• 符合「最优子结构」原则：DP 状态最优值由更小规模的 DP 状态最优值推出
• 符合「无后效性」原则：状态的得到方式，不会影响后续其它 DP 状态取值
• 确定「DP 转移方程」
• 分类讨论，细心枚举

最后的最后，希望大家在求解 DP 问题时可以参考上述解题思路，祝大家刷题愉快！

BY / 

本文作者：Gene_Liu

编辑&版式：霍霍

声明：本文归 “力扣” 版权所有，如需转载请联系。文章封面图来源于网络，如有侵权联系删除。

推荐阅读

1、

2、

3、

4、

5、

如果觉得文章不错，帮忙点个在看呗