R语言案例：Wineind萄葡酒销量预测

Posted 2021-04-18 数之何

选自《R语言预测实战》章节。

        经过上一节的介绍相信各位读者已经知道如何安装R及R程序包。本节拟通过一个简单的例子说明用R语言进行预测的主要步骤，旨在让各位读者了解用R语言进行预测的基本过程。本例使用forecast包中自带的数据集wineind，它表示从1980年1月到1994年8月，由葡萄酒生产商销售的容量不到1升的澳大利亚酒的总量。数据示意如下：

    从数据中可知，这是典型的时间序列数据，一行表示一年，12列表示一年的12个月，按顺序整理的数据。将时间序列绘制如图1-3-20所示。

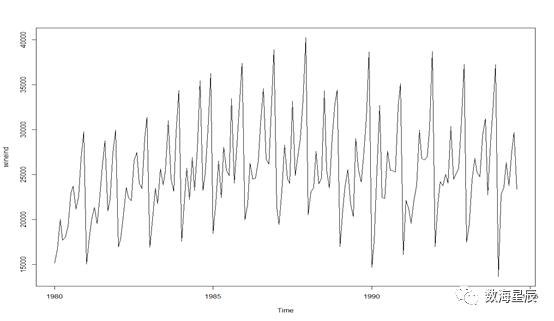
图1-3-20 葡萄酒销售量时间序列

从图中明显可以看出，该时间序列数据呈明显地周期性变化。

数据读入及处理

    加载forecast包，使用自带数据集wineind。使用ACF函数查看wineind数据的自相关性，代码如下：

#读入数据library(forecast)acf(wineind,lag.max=100)

得图1-3-21如下。

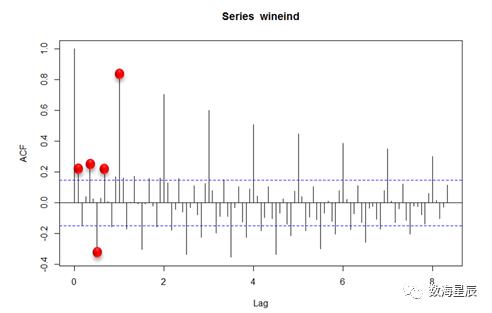
图1-3-21 wineind数据的自相关图

        红点部分为自相关性比较明显的位置，可以初步使用近1、4、6、8、12期的数值建立指标，作为预测基础数据。另外，通过观察确定wineind的数据周期为一年，将1980年到1993年每年按月的曲线图在一张图中，进一步观察，相应代码为：

#观察曲线簇len=1993-1980+1data0=wineind[1:12*len]range0=range(data0)+c(-100,100)plot(1:12,1:12,ylim=range0,col='white',xlab="月份",ylab="销量")for(iin1:len){ points(1:12,wineind[(12*(i-1)+1):(12*i)]) lines(1:12,wineind[(12*(i-1)+1):(12*i)],lty=2)}

相应图参见图1-3-22。

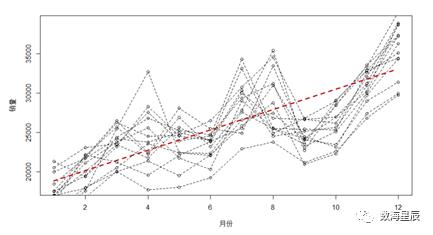
图1-3-22 wineind数据与月份的关系图

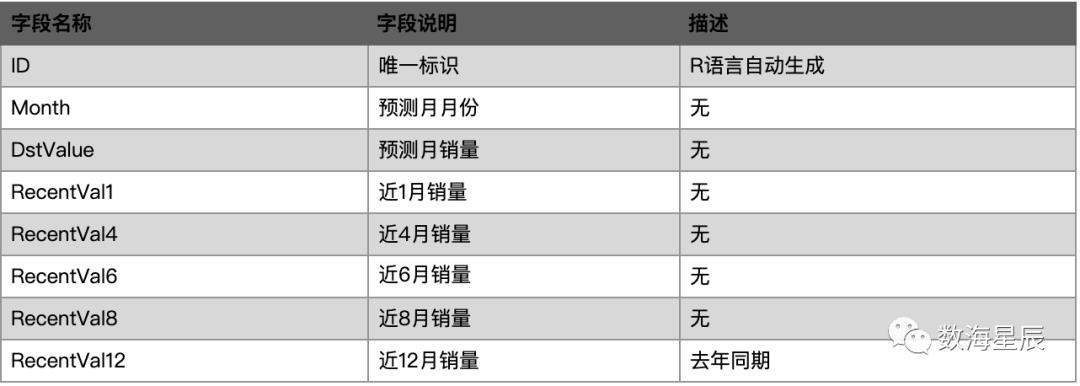
      由图可知，月份与销量线性关系明显，应该考虑进建模基础数据，用于预测。至此，需要将wineind的原始数据，处理成如表1-3-2所示格式，输出建模基础数据集。

表1-3-2 基础数据集属性配置表

数据转换的代码如下：

#对数据按指定格式进行转换Month=NULLDstValue=NULLRecentVal1=NULLRecentVal4=NULLRecentVal6=NULLRecentVal8=NULLRecentVal12=NULL#替换掉太大或太小的值wineind[wineind<18000]=18000wineind[wineind>38000]=38000for(iin(12+1):(length(wineind)-1)){ Month<-c(Month,i%%12+1) DstValue<-c(DstValue,wineind[i+1]) RecentVal1<-c(RecentVal1,wineind[i]) RecentVal4<-c(RecentVal4,wineind[i-3]) RecentVal6<-c(RecentVal6,wineind[i-5]) RecentVal8<-c(RecentVal8,wineind[i-7]) RecentVal12<-c(RecentVal12,wineind[i-11])}preData=data.frame(Month,DstValue,RecentVal1,RecentVal4,RecentVal6,RecentVal8,RecentVal12)head(preData)## Month DstValue RecentVal1 RecentVal4 RecentVal6 RecentVal8 RecentVal12## 1 2 18000 18000 22591 23739 19227 18000## 2 3 20008 18000 26786 21133 22893 20016## 3 4 21354 20008 29740 22591 23739 18000## 4 5 19498 21354 18000 26786 21133 18019## 5 6 22125 19498 18000 29740 22591 19227## 6 7 25817 22125 20008 18000 26786 22893#画出散点矩阵图plot(preData)

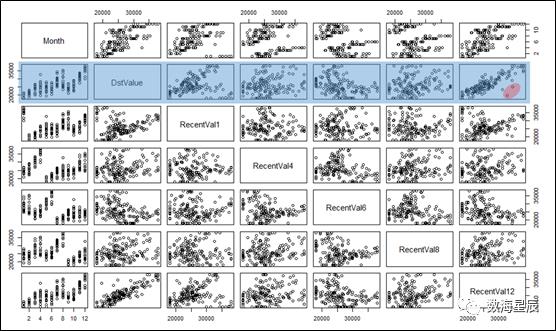
图1-3-23 散点矩阵图

    注意到红圈部分，圈出了两个点，在建模之前需要去掉这两个点，因为这样杠杆点很影响线性模型的建模效果。建立DstValue与RecentVal12的线性模型，通过cooks.distance函数计算每行记录对模拟的影响度量，代码如下：

#使用DstValue与RecentVal12拟合线性模型lm.fit=lm(DstValue~RecentVal12,data=preData)cook<-cooks.distance(lm.fit)plot(cook)abline(h=0.15,lty=2,col='red')

图1-3-24 分离杠杆点

cook[cook>0.15]## 79 123## 0.1706335 0.2433219## 去掉79和123行记录preData=preData[-c(123,79),]

建立模型

    根据上一步输出的基础数据，提取150行作为训练数据，剩下的数据作为测试数据。数据分割及建模的代码如下：

# 分离训练集与测试集trainData=preData[1:150,]testData=preData[151:163,]# 建立模型lm.fit<-lm(DstValue~Month+RecentVal1+RecentVal4+RecentVal6+RecentVal8+RecentVal12,data=trainData)summary(lm.fit)#### Call:## lm(formula = DstValue ~ Month + RecentVal1 + RecentVal4 + RecentVal6 +## RecentVal8 + RecentVal12, data = trainData)#### Residuals:## Min 1Q Median 3Q Max## -4806.5 -1549.1 -171.8 1368.7 6763.3#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 2.214e+03 1.987e+03 1.114 0.26714## Month 3.855e+02 8.955e+01 4.305 3.08e-05 ***## RecentVal1 -2.964e-03 3.354e-02 -0.088 0.92971## RecentVal4 7.227e-02 3.567e-02 2.026 0.04463 *## RecentVal6 -1.825e-02 3.759e-02 -0.486 0.62804## RecentVal8 1.123e-01 3.903e-02 2.876 0.00464 **## RecentVal12 6.701e-01 5.921e-02 11.316 < 2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 1989 on 143 degrees of freedom## Multiple R-squared: 0.848, Adjusted R-squared: 0.8416## F-statistic: 133 on 6 and 143 DF, p-value: < 2.2e-16

      可以看到，调整后的R平方达到0.84，作为模型来讲，基本可以使用。但是看下误差项(Intercept)的P值为0.26714，不显著。所以，目前的模型还需要进一步调整，使得误差项(Intercept)的P值低于0.05或0.01为止。另外，变量RecentVal1 和RecentVal6的P值都较大，明显不显著，考虑了变量之间的相互影响，暂时保留。几个变量中，除了RecentVal12与目标变量呈现比较明显的线性关系外，其它变量跟目标变量的线性关系并不明显。为了让模型拟合得更好，现在开始尝试非线性的方法。由于变量RecentVal1 和RecentVal6对目标变量的影响不明显。这里主要考虑Month、RecentVal4、RecentVal8三个变量对目标变量的非线性影响。在所有的非线性方法中，多项式比较适合单个变量的衍生变换。因此，这里对Month、RecentVal4、RecentVal8三个变量使用多项式的方法，尝试最高次数为5的情况下，模型的拟合情况。代码如下：

# 对Month、RecentVal4、RecentVal8三个变量按5次多项式进行衍生lm.fit<-lm(DstValue~Month+I(Month^2)+I(Month^3)+I(Month^4)+I(Month^5)+RecentVal1+RecentVal4+I(RecentVal4^2)+I(RecentVal4^3)+I(RecentVal4^4)+I(RecentVal4^5)+RecentVal6+RecentVal8+I(RecentVal8^2)+I(RecentVal8^3)+I(RecentVal8^4)+I(RecentVal8^5)+RecentVal12,data=trainData)summary(lm.fit)#### Call:## lm(formula = DstValue ~ Month + I(Month^2) + I(Month^3) + I(Month^4) +## I(Month^5) + RecentVal1 + RecentVal4 + I(RecentVal4^2) +## I(RecentVal4^3) + I(RecentVal4^4) + I(RecentVal4^5) + RecentVal6 +## RecentVal8 + I(RecentVal8^2) + I(RecentVal8^3) + I(RecentVal8^4) +## I(RecentVal8^5) + RecentVal12, data = trainData)#### Residuals:## Min 1Q Median 3Q Max## -4058.4 -1223.1 0.3 1178.7 4386.0#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 4.420e+05 8.389e+05 0.527 0.5992## Month 7.166e+03 4.803e+03 1.492 0.1381## I(Month^2) -2.775e+03 1.974e+03 -1.406 0.1621## I(Month^3) 5.143e+02 3.558e+02 1.446 0.1507## I(Month^4) -4.366e+01 2.893e+01 -1.509 0.1336## I(Month^5) 1.378e+00 8.671e-01 1.589 0.1144## RecentVal1 5.421e-02 5.838e-02 0.928 0.3549## RecentVal4 9.451e+01 1.099e+02 0.860 0.3913## I(RecentVal4^2) -7.444e-03 8.323e-03 -0.894 0.3728## I(RecentVal4^3) 2.888e-07 3.103e-07 0.930 0.3538## I(RecentVal4^4) -5.522e-12 5.699e-12 -0.969 0.3343## I(RecentVal4^5) 4.168e-17 4.124e-17 1.011 0.3140## RecentVal6 -8.917e-02 4.276e-02 -2.085 0.0390 *## RecentVal8 -1.844e+02 1.119e+02 -1.649 0.1016## I(RecentVal8^2) 1.456e-02 8.468e-03 1.720 0.0878 .## I(RecentVal8^3) -5.620e-07 3.155e-07 -1.781 0.0772 .## I(RecentVal8^4) 1.062e-11 5.789e-12 1.835 0.0687 .## I(RecentVal8^5) -7.884e-17 4.186e-17 -1.883 0.0619 .## RecentVal12 5.546e-01 6.477e-02 8.564 2.59e-14 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 1841 on 131 degrees of freedom## Multiple R-squared: 0.8806, Adjusted R-squared: 0.8642## F-statistic: 53.7 on 18 and 131 DF, p-value: < 2.2e-16## 由于涉及到变量太多，使用逐步回归删除掉影响小的变量lm.fit<-step(lm.fit)## 省略。summary(lm.fit)#### Call:## lm(formula = DstValue ~ Month + I(Month^4) + I(Month^5) + I(RecentVal4^3) +## I(RecentVal4^4) + I(RecentVal4^5) + RecentVal6 + RecentVal8 +## I(RecentVal8^2)+ I(RecentVal8^3) + I(RecentVal8^4) + I(RecentVal8^5) +## RecentVal12, data = trainData)#### Residuals:## Min 1Q Median 3Q Max## -4314.5 -1268.5 -66.1 1182.6 4833.0#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 1.083e+06 5.685e+05 1.905 0.058858 .## Month 8.798e+02 2.612e+02 3.368 0.000984 ***## I(Month^4) -1.704e+00 7.587e-01 -2.246 0.026346 *## I(Month^5) 1.328e-01 5.549e-02 2.394 0.018030 *## I(RecentVal4^3) 1.816e-09 1.138e-09 1.595 0.112945## I(RecentVal4^4) -1.022e-13 5.913e-14 -1.728 0.086269 .## I(RecentVal4^5) 1.500e-18 8.052e-19 1.863 0.064676 .## RecentVal6 -9.925e-02 3.953e-02 -2.511 0.013213 *## RecentVal8 -2.143e+02 1.095e+02 -1.958 0.052266 .## I(RecentVal8^2) 1.669e-02 8.295e-03 2.012 0.046187 *## I(RecentVal8^3) -6.364e-07 3.094e-07 -2.057 0.041585 *## I(RecentVal8^4) 1.190e-11 5.681e-12 2.095 0.038006 *## I(RecentVal8^5) -8.747e-17 4.111e-17 -2.127 0.035187 *## RecentVal12 5.561e-01 6.317e-02 8.803 5.39e-15 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 1832 on 136 degrees of freedom## Multiple R-squared: 0.8773, Adjusted R-squared: 0.8656## F-statistic: 74.81 on 13 and 136 DF, p-value: < 2.2e-16

去掉P值较大的三个变量I(RecentVal4^3)、I(RecentVal4^4)、I(RecentVal4^5)后，再拟合一次模型，代码如下：

lm.fit<-lm(formula=DstValue~Month+I(Month^4)+I(Month^5)+RecentVal6+RecentVal8+I(RecentVal8^2)+I(RecentVal8^3)+I(RecentVal8^4)+I(RecentVal8^5)+RecentVal12,data=trainData)summary(lm.fit)#### Call:## lm(formula = DstValue ~ Month + I(Month^4) + I(Month^5) + RecentVal6 +## RecentVal8 + I(RecentVal8^2) + I(RecentVal8^3) + I(RecentVal8^4) +## I(RecentVal8^5) + RecentVal12, data = trainData)#### Residuals:## Min 1Q Median 3Q Max## -4244.9 -1295.2 -32.6 1174.8 7125.9#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 1.345e+06 5.659e+05 2.377 0.01879 *## Month 8.941e+02 2.072e+02 4.316 3.00e-05 ***## I(Month^4) -1.824e+00 6.404e-01 -2.847 0.00508 **## I(Month^5) 1.417e-01 4.771e-02 2.969 0.00352 **## RecentVal6 -9.957e-02 3.872e-02 -2.571 0.01118 *## RecentVal8 -2.649e+02 1.087e+02 -2.436 0.01611 *## I(RecentVal8^2) 2.058e-02 8.228e-03 2.501 0.01354 *## I(RecentVal8^3) -7.838e-07 3.064e-07 -2.558 0.01160 *## I(RecentVal8^4) 1.466e-11 5.619e-12 2.608 0.01009 *## I(RecentVal8^5) -1.077e-16 4.061e-17 -2.653 0.00892 **## RecentVal12 5.629e-01 6.377e-02 8.827 4.12e-15 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 1874 on 139 degrees of freedom## Multiple R-squared: 0.8688, Adjusted R-squared: 0.8593## F-statistic: 92.02 on 10 and 139 DF, p-value: < 2.2e-16

如上为本次拟合的结果，所有系数的P值都小于0.05，影响明显，且拟合优度为0.86，可用于预测。lm.fit就是我们建立的用于时间序列预测的线性回归模型。

预测及误差分析

用lm.fit作为预测模型，对预测数据源testData进行预测。代码如下：

## 对新数据进行预测testData$pred=predict(lm.fit,testData)## 计算百分误差率testData$diff=abs(testData$DstValue-testData$pred)/testData$DstValuetestData## Month DstValue RecentVal1 RecentVal4 RecentVal6 RecentVal8 RecentVal12## 153 10 28496 22724 24735 26805 19463 25650## 154 11 32857 28496 29356 25236 24352 30923## 155 12 37198 32857 31234 24735 26805 37240## 156 1 18000 37198 22724 29356 25236 18000## 157 2 22784 18000 28496 31234 24735 19463## 158 3 23565 22784 32857 22724 29356 24352## 159 4 26323 23565 37198 28496 31234 26805## 160 5 23779 26323 18000 32857 22724 25236## 161 6 27549 23779 22784 37198 28496 24735## 162 7 29660 27549 23565 18000 32857 29356## 163 8 23356 29660 26323 22784 37198 31234## pred diff## 153 25154.08 0.117276814## 154 31448.29 0.042874098## 155 37063.76 0.003608861## 156 18724.46 0.040247684## 157 20238.79 0.111710356## 158 24022.79 0.019426610## 159 25778.01 0.020704134## 160 24900.35 0.047157117## 161 24405.94 0.114089645## 162 30005.15 0.011636800## 163 30888.46 0.322506541summary(testData)## Month DstValue RecentVal1 RecentVal4## Min. : 1.000 Min. :18000 Min. :18000 Min. :18000## 1st Qu.: 3.500 1st Qu.:23461 1st Qu.:23175 1st Qu.:23175## Median : 6.000 Median :26323 Median :26323 Median :26323## Mean : 6.273 Mean :26688 Mean :26630 Mean :27025## 3rd Qu.: 9.000 3rd Qu.:29078 3rd Qu.:29078 3rd Qu.:30295## Max. :12.000 Max. :37198 Max. :37198 Max. :37198## RecentVal6 RecentVal8 RecentVal12 pred## Min. :18000 Min. :19463 Min. :18000 Min. :18724## 1st Qu.:23760 1st Qu.:24544 1st Qu.:24544 1st Qu.:24214## Median :26805 Median :26805 Median :25650 Median :25154## Mean :27220 Mean :27496 Mean :26636 Mean :26603## 3rd Qu.:30295 3rd Qu.:30295 3rd Qu.:30140 3rd Qu.:30447## Max. :37198 Max. :37198 Max. :37240 Max. :37064## diff## Min. :0.003609## 1st Qu.:0.020065## Median :0.042874## Mean :0.077385## 3rd Qu.:0.112900## Max. :0.322506

       从统计结果中，可以看到，对预测数据集共11条记录进行预测，最小百分误差率为0.36%，最大百分误差率为32.25%，平均百分误差率为7.73%。预测结果还是很不错的，除了最后一条记录，预测值为30888.46，取整为30888与真实结果23356差别较大，根据笔者的经验，该月可能遇到什么特殊情况（如气象灾害导致葡萄收成不好等），导致高估了葡萄酒的销量。当预测不准时，不见得都是模型的问题，有可能是数据的问题，这时需要从数据中去发现问题，并进一步解决问题，预测的目的就是为了改变。有兴趣的读者，还可以使用纵横两年的数据关系，构建指标体系，有望对模型进一步优化。