使用R语言进行时间序列（arima，指数平滑）分析

Posted 2021-04-18 拓端数据部落

原文：http://tecdat.cn/?p=3609

 

读时间序列数据

您要分析时间序列数据的第一件事就是将其读入R，并绘制时间序列。您可以使用scan（）函数将数据读入R，该函数假定连续时间点的数据位于包含一列的简单文本文件中。

 

数据集如下所示：

Age of Death of Successive Kings of England#starting with William the Conqueror#Source: McNeill, "Interactive Data Analysis"604367505642506568436534...

仅显示了文件的前几行。前三行包含对数据的一些注释，当我们将数据读入R时我们想要忽略它。我们可以通过使用scan（）函数的“skip”参数来使用它，它指定了多少行。要忽略的文件顶部。要将文件读入R，忽略前三行，我们键入：

> kings[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56

在这种情况下，英国42位连续国王的死亡年龄已被读入变量“国王”。

一旦将时间序列数据读入R，下一步就是将数据存储在R中的时间序列对象中，这样就可以使用R的许多函数来分析时间序列数据。要将数据存储在时间序列对象中，我们使用R中的ts（）函数。例如，要将数据存储在变量'kings'中作为R中的时间序列对象，我们键入：

Time Series:Start = 1End = 42Frequency = 1[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56

有时，您所拥有的时间序列数据集可能是以不到一年的固定间隔收集的，例如，每月或每季度。在这种情况下，您可以使用ts（）函数中的'frequency'参数指定每年收集数据的次数。对于月度时间序列数据，您设置频率= 12，而对于季度时间序列数据，您设置频率= 4。

您还可以使用ts（）函数中的“start”参数指定收集数据的第一年和该年度的第一个时间间隔。例如，如果第一个数据点对应于1986年第二季度，则设置start = c（1986,2）。

 

> birthstimeseries <- ts(births, frequency=12, start=c(1946,1))> birthstimeseriesJan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec1946 26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.901 23.175 23.227 21.672 21.8701947 21.439 21.089 23.709 21.669 21.752 20.761 23.479 23.824 23.105 23.110 21.759 22.0731948 21.937 20.035 23.590 21.672 22.222 22.123 23.950 23.504 22.238 23.142 21.059 21.5731949 21.548 20.000 22.424 20.615 21.761 22.874 24.104 23.748 23.262 22.907 21.519 22.0251950 22.604 20.894 24.677 23.673 25.320 23.583 24.671 24.454 24.122 24.252 22.084 22.9911951 23.287 23.049 25.076 24.037 24.430 24.667 26.451 25.618 25.014 25.110 22.964 23.9811952 23.798 22.270 24.775 22.646 23.988 24.737 26.276 25.816 25.210 25.199 23.162 24.7071953 24.364 22.644 25.565 24.062 25.431 24.635 27.009 26.606 26.268 26.462 25.246 25.1801954 24.657 23.304 26.982 26.199 27.210 26.122 26.706 26.878 26.152 26.379 24.712 25.6881955 24.990 24.239 26.721 23.475 24.767 26.219 28.361 28.599 27.914 27.784 25.693 26.8811956 26.217 24.218 27.914 26.975 28.527 27.139 28.982 28.169 28.056 29.136 26.291 26.9871957 26.589 24.848 27.543 26.896 28.878 27.390 28.065 28.141 29.048 28.484 26.634 27.7351958 27.132 24.924 28.963 26.589 27.931 28.009 29.229 28.759 28.405 27.945 25.912 26.6191959 26.076 25.286 27.660 25.951 26.398 25.565 28.865 30.000 29.261 29.012 26.992 27.897

同样，  1987年1月至1993年12月澳大利亚昆士兰州海滩度假小镇纪念品商店的月销售额（来自Wheelwright和Hyndman的原始数据， 1998）。我们可以通过输入以下内容将数据读入R：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
   
 
   
Read 84 items> souvenirtimeseries <- ts(souvenir, frequency=12, start=c(1987,1))> souvenirtimeseriesJan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec1987 1664.81 2397.53 2840.71 3547.29 3752.96 3714.74 4349.61 3566.34 5021.82 6423.48 7600.60 19756.211988 2499.81 5198.24 7225.14 4806.03 5900.88 4951.34 6179.12 4752.15 5496.43 5835.10 12600.08 28541.721989 4717.02 5702.63 9957.58 5304.78 6492.43 6630.80 7349.62 8176.62 8573.17 9690.50 15151.84 34061.011990 5921.10 5814.58 12421.25 6369.77 7609.12 7224.75 8121.22 7979.25 8093.06 8476.70 17914.66 30114.411991 4826.64 6470.23 9638.77 8821.17 8722.37 10209.48 11276.55 12552.22 11637.39 13606.89 21822.11 45060.691992 7615.03 9849.69 14558.40 11587.33 9332.56 13082.09 16732.78 19888.61 23933.38 25391.35 36024.80 80721.711993 10243.24 11266.88 21826.84 17357.33 15997.79 18601.53 26155.15 28586.52 30505.41 30821.33 46634.38 104660.67
 
  

绘制时间序列

一旦你将时间序列读入R，下一步通常是制作时间序列数据的图，你可以用R中的plot.ts（）函数做。

例如，为了绘制英国42位连续国王的死亡时间序列，我们输入：

> plot.ts(kingstimeseries)

我们可以从时间图中看出，可以使用加性模型来描述该时间序列，因为数据中的随机波动在大小上随时间大致恒定。

同样，为了绘制纽约市每月出生人数的时间序列，我们输入：

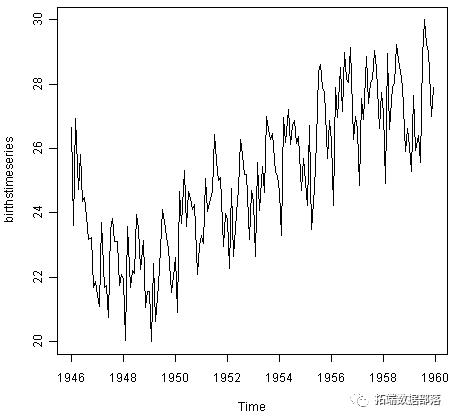
从这个时间序列我们可以看出，每月出生人数似乎有季节性变化：每年夏天都有一个高峰，每个冬天都有一个低谷。同样，似乎这个时间序列可能是用加性模型来描述的，因为季节性波动的大小随着时间的推移大致不变，似乎并不依赖于时间序列的水平，随机波动似乎也是随着时间的推移大小不变。

同样，为了绘制澳大利亚昆士兰州海滩度假小镇纪念品商店每月销售的时间序列，我们输入：

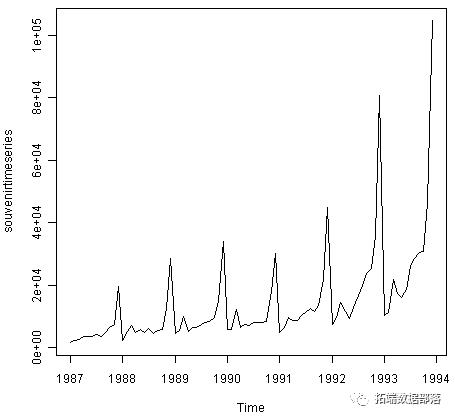
在这种情况下，似乎加法模型不适合描述这个时间序列，因为季节性波动和随机波动的大小似乎随着时间序列的水平而增加。因此，我们可能需要转换时间序列以获得可以使用加法模型描述的变换时间序列。例如，我们可以通过计算原始数据的自然日志来转换时间序列：

 > plot.ts(logsouvenirtimeseries)

在这里我们可以看到，对数变换时间序列中的季节性波动和随机波动的大小似乎随着时间的推移大致不变，并且不依赖于时间序列的水平。因此，可以使用加法模型来描述对数变换的时间序列。

分解时间序列

分解时间序列意味着将其分成其组成部分，这些组成部分通常是趋势分量和不规则分量，如果是季节性时间序列，则是季节性分量。

分解非季节性数据

非季节性时间序列由趋势分量和不规则分量组成。分解时间序列涉及尝试将时间序列分成这些分量，即估计趋势分量和不规则分量。

为了估计可以使用加性模型描述的非季节性时间序列的趋势分量，通常使用平滑方法，例如计算时间序列的简单移动平均值。

“TTR”R包中的SMA（）函数可用于使用简单的移动平均值来平滑时间序列数据。要使用此功能，我们首先需要安装“TTR”R软件包 。一旦安装了“TTR”R软件包，就可以输入以下命令加载“TTR”R软件包：

然后，您可以使用“SMA（）”功能来平滑时间序列数据。要使用SMA（）函数，需要使用参数“n”指定简单移动平均值的顺序（跨度）。例如，要计算5阶的简单移动平均值，我们在SMA（）函数中设置n = 5。

例如，如上所述，英国42位连续国王的死亡年龄的时间序列出现是非季节性的，并且可能使用加性模型来描述，因为数据中的随机波动大小基本上是恒定的。时间：

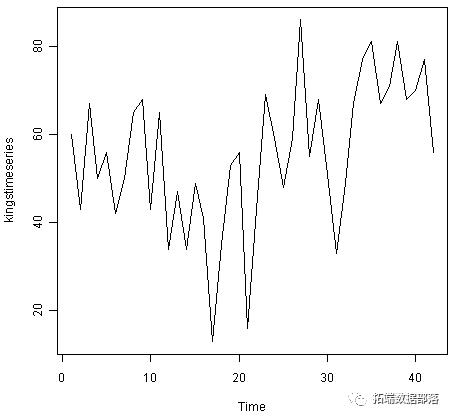
因此，我们可以尝试通过使用简单移动平均线进行平滑来估计此时间序列的趋势分量。要使用3阶简单移动平均值平滑时间序列，并绘制平滑时间序列数据，我们键入：

> kingstimeseriesSMA3 <- SMA(kingstimeseries,n=3)> plot.ts(kingstimeseriesSMA3)

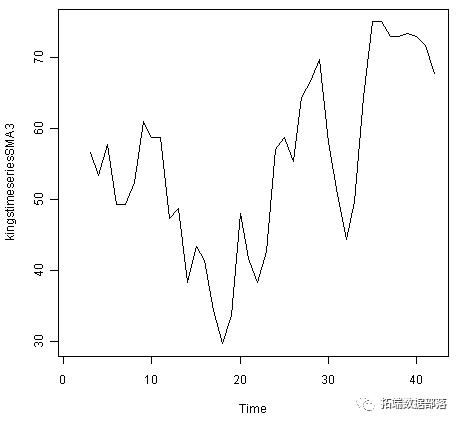
在使用3阶简单移动平均值平滑的时间序列中，似乎存在相当多的随机波动。因此，为了更准确地估计趋势分量，我们可能希望尝试使用简单的移动平均值来平滑数据。更高阶。这需要一些试错，才能找到合适的平滑量。例如，我们可以尝试使用8阶的简单移动平均线：

  
    
    
  
 
   
 
    
 
    
 
   
 
   
> kingstimeseriesSMA8 <- SMA(kingstimeseries,n=8)> plot.ts(kingstimeseriesSMA8)
 
  

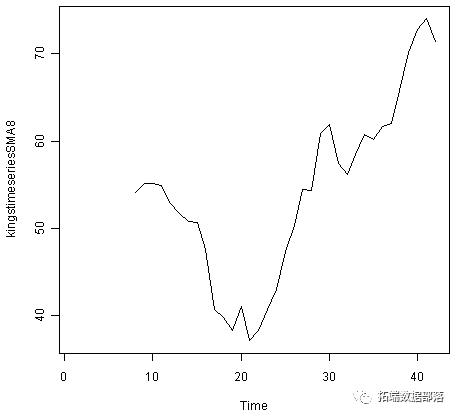
使用8阶简单移动平均值进行平滑的数据可以更清晰地显示趋势分量，我们可以看到英国国王的死亡年龄似乎已经从大约55岁降至大约38岁在最后的20位国王中，然后在第40位国王在时间序列的统治结束之后增加到大约73岁。

分解季节性数据

季节性时间序列由趋势组件，季节性组件和不规则组件组成。分解时间序列意味着将时间序列分成这三个组成部分：即估计这三个组成部分。

为了估计可以使用加性模型描述的季节性时间序列的趋势分量和季节性分量，我们可以使用R中的“decompose（）”函数。该函数估计时间序列的趋势，季节和不规则分量。可以使用加性模型来描述。

函数“decompose（）”返回一个列表对象作为结果，其中季节性组件，趋势组件和不规则组件的估计值存储在该列表对象的命名元素中，称为“季节性”，“趋势”和“随机” “ 分别。

例如，如上所述，纽约市每月出生人数的时间序列是季节性的，每年夏季和每年冬季都会出现高峰，并且可能使用加性模型来描述，因为季节性和随机波动似乎是随着时间的推移大小不变：

为了估计这个时间序列的趋势，季节性和不规则成分，我们输入：

  
    
    
  
 
   
 
    
 
    
 
   
 
   
> birthstimeseriescomponents <- decompose(birthstimeseries)
 
  

季节性，趋势和不规则成分的估计值现在存储在变量birthstimeseriescomponents $ seasonal，birthstimeseriescomponents $ trend和birthstimeseriescomponents $ random中。例如，我们可以通过键入以下内容打印出季节性组件的估计值：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
   
 
   
> birthstimeseriescomponents$seasonal # get the estimated values of the seasonal componentJan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec1946 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971947 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971948 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971949 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971950 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971951 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971952 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971953 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971954 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971955 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971956 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971957 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971958 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938 0.6916162 0.7752444 -1.1097652 -0.37681971959 -0.6771947 -2.0829607 0.8625232 -0.8016787 0.2516514 -0.1532556 1.4560457 1.1645938
 
  

估计的季节性因素是在1月至12月期间给出的，并且每年都是相同的。最大的季节性因素是7月份（约1.46），最低的是2月份（约-2.08），表明7月出生率似乎达到高峰，2月出生低谷。

我们可以使用“plot（）”函数绘制时间序列的估计趋势，季节和不规则分量，例如：

> plot(birthstimeseriescomponents)

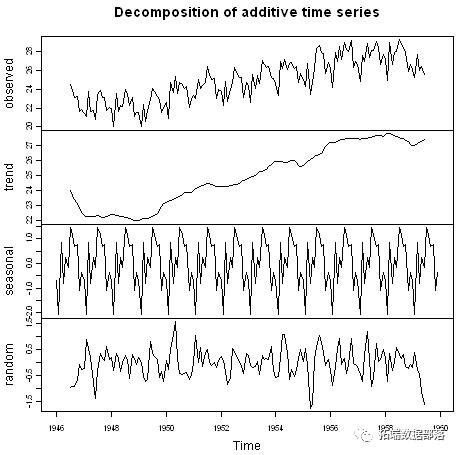
上图显示了原始时间序列（顶部），估计趋势分量（从顶部开始的第二个），估计的季节性分量（从顶部开始的第三个）和估计的不规则分量（底部）。我们看到估计的趋势分量显示从1947年的大约24小幅下降到1948年的大约22小幅下降，随后从1959年开始稳步增加到大约27。

季节性调整

如果您有可以使用附加模型描述的季节性时间序列，则可以通过估计季节性成分来季节性地调整时间序列，并从原始时间序列中减去估计的季节性成分。我们可以使用“decompose（）”函数计算的季节性成分的估计来做到这一点。

例如，要季节性调整纽约市每月出生人数的时间序列，我们可以使用“decompose（）”估算季节性成分，然后从原始时间序列中减去季节性成分：

  
    
    
  
 
   
 
    
 
    
 
    
 
   
 
   
> birthstimeseriescomponents <- decompose(birthstimeseries)> birthstimeseriesseasonallyadjusted <- birthstimeseries - birthstimeseriescomponents$seasonal
 
  

然后我们可以使用“plot（）”函数绘制经季节性调整的时间序列，输入：

> plot(birthstimeseriesseasonallyadjusted)

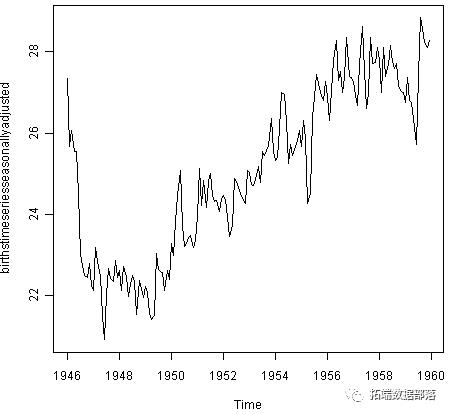
您可以看到季节性变化已从经季节性调整的时间序列中删除。经季节性调整的时间序列现在只包含趋势分量和不规则分量。

使用指数平滑的预测

指数平滑可用于对时间序列数据进行短期预测。

简单的指数平滑

如果您有一个时间序列可以使用具有恒定水平且没有季节性的附加模型来描述，则可以使用简单的指数平滑来进行短期预测。

简单指数平滑方法提供了一种估计当前时间点的水平的方法。平滑由参数alpha控制; 用于估计当前时间点的水平。alpha的值; α值接近于0意味着在对未来值进行预测时，最近的观察值很小。

 

Read 100 items> rainseries <- ts(rain,start=c(1813))> plot.ts(rainseries)

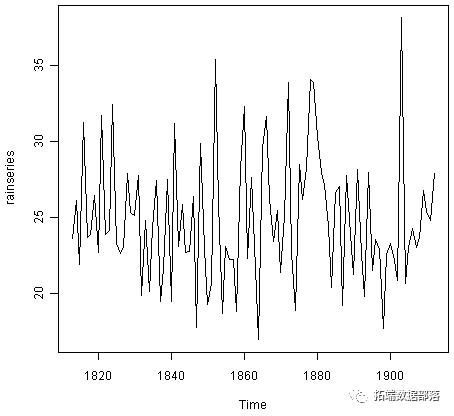
你可以从图中看到大致恒定的水平（平均值保持恒定在25英寸左右）。随着时间的推移，时间序列中的随机波动似乎大致不变，因此使用加性模型描述数据可能是合适的。因此，我们可以使用简单的指数平滑进行预测。

为了使用R中的简单指数平滑进行预测，我们可以使用R中的“HoltWinters（）”函数拟合一个简单的指数平滑预测模型。要使用HoltWinters（）进行简单的指数平滑，我们需要设置参数beta = FALSE和HoltWinters（）函数中的gamma = FALSE（β和gamma参数用于Holt的指数平滑，或Holt-Winters指数平滑，如下所述）。

HoltWinters（）函数返回一个列表变量，该变量包含多个命名元素。

例如，要使用简单的指数平滑来预测伦敦年降雨量的时间序列，我们输入：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
   
 
   
> rainseriesforecasts <- HoltWinters(rainseries, beta=FALSE, gamma=FALSE)> rainseriesforecastsSmoothing parameters:alpha: 0.02412151beta : FALSEgamma: FALSECoefficients:[,1]a 24.67819
 
  
HoltWinters（）的输出告诉我们alpha参数的估计值约为0.024。这非常接近零，告诉我们预测是基于最近和最近的观察结果（虽然对最近的观察更加重视）。

默认情况下，HoltWinters（）仅对我们原始时间序列所涵盖的相同时间段进行预测。在这种情况下，我们的原始时间序列包括1813年至1912年伦敦的降雨量，所以预测也是1813年至1912年。

在上面的例子中，我们将HoltWinters（）函数的输出存储在列表变量“rainseriesforecasts”中。HoltWinters（）的预测存储在这个名为“fits”的列表变量的命名元素中，因此我们可以通过输入以下内容来获取它们的值：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
   
 
   
> rainseriesforecasts$fittedTime Series:Start = 1814End = 1912Frequency = 1xhat level1814 23.56000 23.560001815 23.62054 23.620541816 23.57808 23.578081817 23.76290 23.762901818 23.76017 23.760171819 23.76306 23.763061820 23.82691 23.82691...1905 24.62852 24.628521906 24.58852 24.588521907 24.58059 24.580591908 24.54271 24.542711909 24.52166 24.521661910 24.57541 24.575411911 24.59433 24.594331912 24.59905 24.59905
 
  
我们可以通过键入以下内容来绘制原始时间序列与预测：

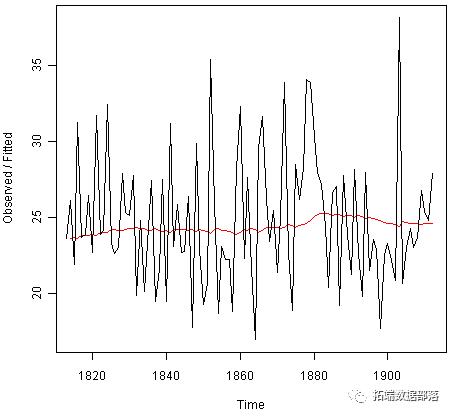
> plot(rainseriesforecasts)

该图显示原始时间序列为黑色，预测显示为红线。预测的时间序列比原始数据的时间序列要平滑得多。

作为预测准确性的度量，我们可以计算样本内预测误差的平方误差之和，即我们原始时间序列所涵盖的时间段的预测误差。平方误差之和存储在名为“SSE”的列表变量“rainseriesforecasts”的命名元素中，因此我们可以通过键入以下内容来获取其值：

  
    
    
  
 
   
 
    
 
    
 
   
 
   
> rainseriesforecasts$SSE[1] 1828.855
 
  
也就是说，这里的平方误差之和为1828.855。

在简单的指数平滑中，通常使用时间序列中的第一个值作为级别的初始值。例如，在伦敦的降雨时间序列中，1813年降雨量的第一个值为23.56（英寸）。您可以使用“l.start”参数指定HoltWinters（）函数中水平的初始值。例如，要将级别的初始值设置为23.56进行预测，我们键入：

> HoltWinters(rainseries, beta=FALSE, gamma=FALSE, l.start=23.56)

如上所述，默认情况下，HoltWinters（）仅对原始数据所涵盖的时间段进行预测，即降雨时间序列为1813-1912。我们可以使用R“forecast”包中的“forecast.HoltWinters（）”函数对更多时间点进行预测。要使用forecast.HoltWinters（）函数，我们首先需要安装“预测”R包（有关如何安装R包的说明，请参阅如何安装R包）。

安装“预测”R软件包后，您可以键入以下命令加载“预测”R软件包：

> library("forecast")

当使用forecast.HoltWinters（）函数作为其第一个参数（输入）时，您将使用HoltWinters（）函数传递给您已经拟合的预测模型。例如，在降雨时间序列的情况下，我们将使用HoltWinters（）的预测模型存储在变量“rainseriesforecasts”中。您可以使用forecast.HoltWinters（）中的“h”参数指定要进行预测的其他时间点数。例如，要使用forecast.HoltWinters（）预测1814-1820（8年以上）的降雨量，我们输入：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
   
 
   
> rainseriesforecasts2 <- forecast.HoltWinters(rainseriesforecasts, h=8)> rainseriesforecasts2Point Forecast Lo 80 Hi 80 Lo 95 Hi 951913 24.67819 19.17493 30.18145 16.26169 33.094701914 24.67819 19.17333 30.18305 16.25924 33.097151915 24.67819 19.17173 30.18465 16.25679 33.099601916 24.67819 19.17013 30.18625 16.25434 33.102041917 24.67819 19.16853 30.18785 16.25190 33.104491918 24.67819 19.16694 30.18945 16.24945 33.106941919 24.67819 19.16534 30.19105 16.24701 33.109381920 24.67819 19.16374 30.19265 16.24456 33.11182
 
  
forecast.HoltWinters（）函数为您提供一年的预测，预测的预测间隔为80％，预测的预测间隔为95％。例如，1920年的预测降雨量约为24.68英寸，95％的预测间隔为（16.24,33.11）。

要绘制forecast.HoltWinters（）所做的预测，我们可以使用“plot.forecast（）”函数：

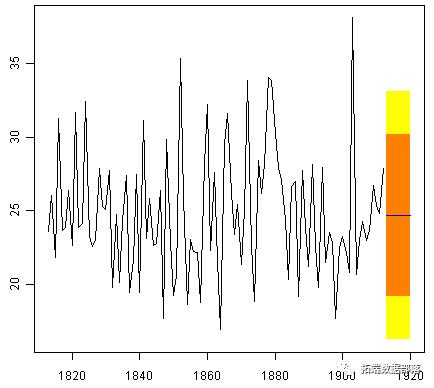
> plot.forecast(rainseriesforecasts2)

这里1913-1920的预测绘制为蓝线，80％预测间隔绘制为橙色阴影区域，95％预测间隔绘制为黄色阴影区域。

对于每个时间点，“预测误差”被计算为观测值减去预测值。我们只能计算原始时间序列所涵盖的时间段的预测误差，即降雨数据的1813-1912。如上所述，预测模型准确性的一个度量是样本内预测误差的平方误差和（SSE）。

样本内预测错误存储在forecast.HoltWinters（）返回的列表变量的命名元素“residuals”中。如果无法改进预测模型，则连续预测的预测误差之间不应存在相关性。换句话说，如果连续预测的预测误差之间存在相关性，则可能通过另一种预测技术可以改进简单的指数平滑预测。

为了弄清楚是否是这种情况，我们可以获得滞后1-20的样本内预测误差的相关图。我们可以使用R中的“acf（）”函数计算预测误差的相关图。要指定我们想要查看的最大滞后，我们在acf（）中使用“lag.max”参数。

例如，为了计算伦敦降雨数据的样本内预测误差的相关图，我们输入：

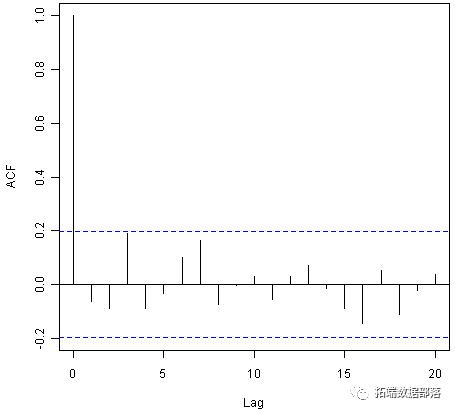
> acf(rainseriesforecasts2$residuals, lag.max=20)

您可以从示例相关图中看到滞后3处的自相关刚刚触及显着边界。为了测试是否存在滞后1-20的非零相关性的重要证据，我们可以进行Ljung-Box测试。这可以使用“Box.test（）”函数在R中完成。我们想要查看的最大延迟是使用Box.test（）函数中的“lag”参数指定的。例如，要测试是否存在滞后1-20的非零自相关，对于伦敦降雨数据的样本内预测误差，我们键入：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
   
 
   
> Box.test(rainseriesforecasts2$residuals, lag=20, type="Ljung-Box")Box-Ljung testdata: rainseriesforecasts2$residualsX-squared = 17.4008, df = 20, p-value = 0.6268
 
  
这里的Ljung-Box检验统计量为17.4，p值为0.6，因此几乎没有证据表明样本预测误差在1-20落后存在非零自相关。

为了确保预测模型无法改进，检查预测误差是否正态分布均值为零和恒定方差也是一个好主意。要检查预测误差是否具有恒定方差，我们可以制作样本内预测误差的时间图：

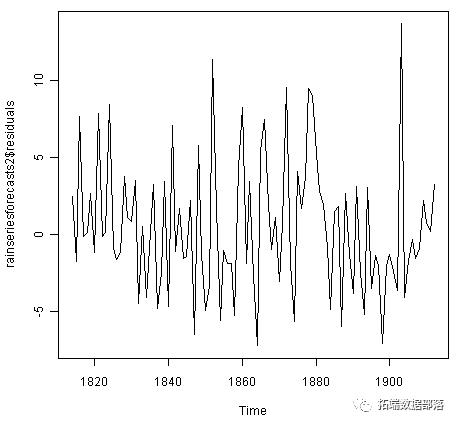
> plot.ts(rainseriesforecasts2$residuals)

该图显示样本内预测误差似乎随时间变化大致不变，尽管时间序列（1820-1830）开始时波动的大小可能略小于后期日期（例如1840年） -1850）。

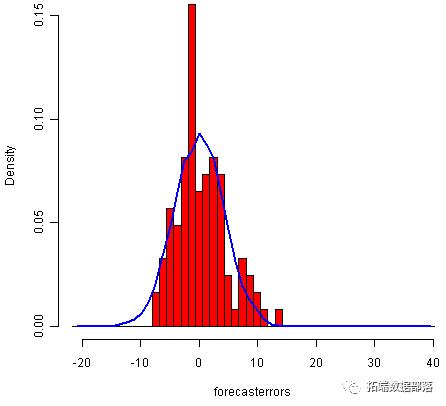
为了检查预测误差是否正态分布为均值为零，我们可以绘制预测误差的直方图，其中覆盖的正态曲线具有平均零和标准差与预测误差的分布相同。为此，我们可以在下面定义一个R函数“plotForecastErrors（）”：

您必须将上述功能复制到R中才能使用它。然后，您可以使用plotForecastErrors（）绘制降雨预测的预测误差的直方图（具有重叠的正常曲线）：

> plotForecastErrors(rainseriesforecasts2$residuals)

该图显示预测误差的分布大致以零为中心，并且或多或少地正态分布，尽管与正常曲线相比，它似乎略微偏向右侧。然而，右倾斜相对较小，因此预测误差通常以均值0分布是合理的。

Ljung-Box测试表明，样本内预测误差中几乎没有非零自相关的证据，预测误差的分布似乎正常分布为均值为零。这表明简单的指数平滑方法为伦敦降雨提供了一个充分的预测模型，这可能无法改进。此外，80％和95％预测区间基于的假设（预测误差中没有自相关，预测误差通常以均值零和恒定方差分布）可能是有效的。

霍尔特的指数平滑

如果您的时间序列可以使用趋势增加或减少且没有季节性的加法模型来描述，则可以使用Holt的指数平滑来进行短期预测。

霍尔特的指数平滑估计当前时间点的水平和斜率。平滑由两个参数α控制，用于估计当前时间点的水平，β用于估计当前时间点的趋势分量的斜率b。与简单的指数平滑一样，参数alpha和beta的值介于0和1之间，接近0的值意味着在对未来值进行预测时，对最近的观察值的重要性很小。

时间序列的一个例子可以使用具有趋势和没有季节性的加法模型来描述女性裙子在1866年到1911年的年度直径的时间序列。 过输入以下内容读入并绘制R中的数据：

  
    
    
  
 
   
 
    
 
    
 
    
 
   
 
   

> skirtsseries <- ts(skirts,start=c(1866))> plot.ts(skirtsseries)
 
  

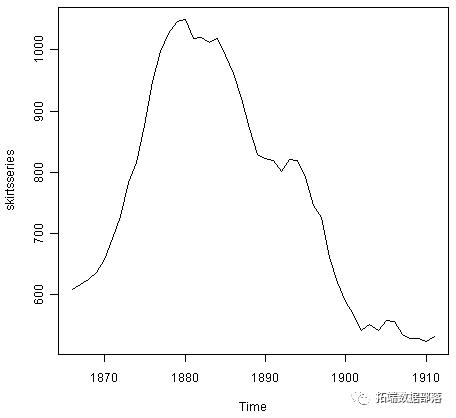
从图中我们可以看出，下摆直径从1866年的约600增加到1880年的约1050，之后在1911年，下摆直径减少到约520。

为了进行预测，我们可以使用R中的HoltWinters（）函数拟合预测模型。要使用HoltWinters（）进行Holt的指数平滑，我们需要设置参数gamma = FALSE（gamma参数用于Holt-Winters指数平滑，如下所述）。

例如，要使用Holt的指数平滑来拟合裙摆直径的预测模型，我们键入：

  
    
    
  
 
   
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
    
 
   
 
   
> skirtsseriesforecasts <- HoltWinters(skirtsseries, gamma=FALSE)> skirtsseriesforecastsSmoothing parameters:alpha: 0.8383481beta : 1gamma: FALSECoefficients:[,1]a 529.308585b 5.690464> skirtsseriesforecasts$SSE[1] 16954.18
 
  
α的估计值为0.84，β的估计值为1.00。这些都很高，告诉我们水平的当前值和趋势分量的斜率b的估计主要基于时间序列中的最近观察。这具有良好的直观感，因为时间序列的水平和斜率都会随着时间的推移而发生很大变化。样本内预测误差的平方和误差的值是16954。

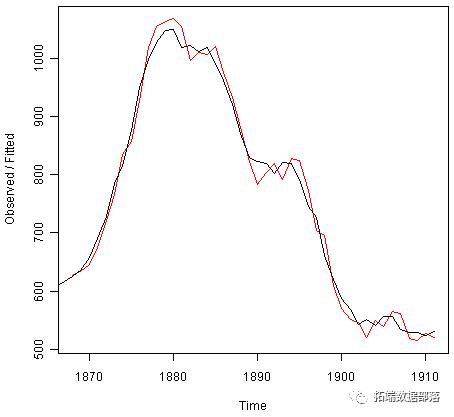
我们可以将原始时间序列绘制为黑色线条，其中预测值为红线，通过键入：

> plot(skirtsseriesforecasts)

我们从图中可以看出，样本内预测与观测值非常吻合，尽管它们往往略微落后于观测值。

如果需要，可以使用HoltWinters（）函数的“l.start”和“b.start”参数指定趋势分量的级别和斜率b的初始值。通常将水平的初始值设置为时间序列中的第一个值（裙边数据为608），并将斜率的初始值设置为第二个值减去第一个值（裙边数据为9）。例如，为了使用Holt的指数平滑拟合裙边折边数据的预测模型，水平的初始值为608，趋势分量的斜率b为9，我们输入：

> HoltWinters(skirtsseries, gamma=FALSE, l.start=608, b.start=9)

对于简单的指数平滑，我们可以使用“forecast”包中的forecast.HoltWinters（）函数对原始时间序列未涵盖的未来时间进行预测。例如，我们的裙摆下摆的时间序列数据是1866年至1911年，因此我们可以预测1912年至1930年（另外19个数据点），并通过输入以下内容绘制：

  
    
    
  
 
   
 
    
 
    
 
   
 
   
> skirtsseriesforecasts2 <- forecast.HoltWinters(skirtsseriesforecasts, h=19)> plot.forecast(skirtsseriesforecasts2)
 
  

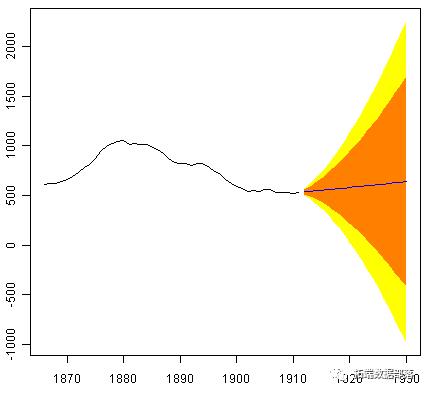
预测显示为蓝线，80％预测区间为橙色阴影区域，95％预测区间为黄色阴影区域。

对于简单的指数平滑，我们可以通过检查样本内预测误差是否在滞后1-20处显示非零自相关来检查是否可以改进预测模型。例如，对于裙边折边数据，我们可以制作一个相关图，并通过键入以下内容来执行Ljung-Box测试：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> acf(skirtsseriesforecasts2$residuals, lag.max=20)> Box.test(skirtsseriesforecasts2$residuals, lag=20, type="Ljung-Box")Box-Ljung testdata: skirtsseriesforecasts2$residualsX-squared = 19.7312, df = 20, p-value = 0.4749
 
    
 
  

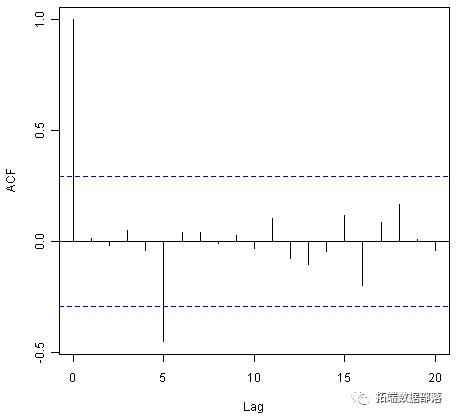
此处相关图显示滞后5处的样本内预测误差的样本自相关超过了显着性边界。然而，我们预计前20个国家中20个自相关中有一个仅仅偶然地超过95％的显着性界限。实际上，当我们进行Ljung-Box检验时，p值为0.47，表明在1-20落后的样本内预测误差中几乎没有证据表明存在非零自相关。

对于简单的指数平滑，我们还应检查预测误差随时间的变化是否恒定，并且通常以均值0分布。我们可以通过制作预测误差的时间图和预测误差分布的直方图以及覆盖的正常曲线来做到这一点：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
     
 
     
> plot.ts(skirtsseriesforecasts2$residuals) # make a time plot> plotForecastErrors(skirtsseriesforecasts2$residuals) # make a histogram
 
    
 
  

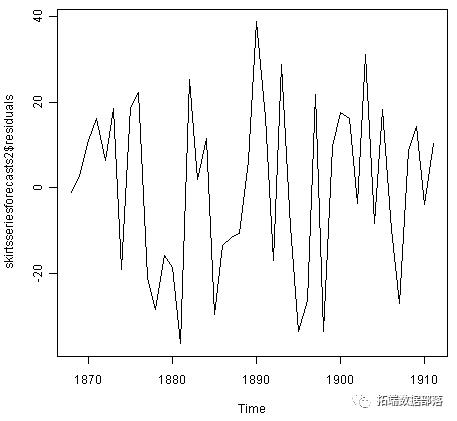
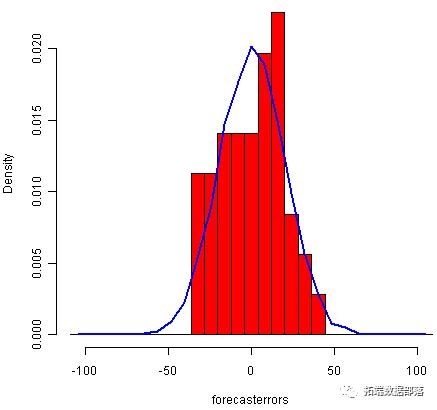
预测误差的时间图表明预测误差随时间变化大致不变。预测误差的直方图表明，预测误差通常以均值零和常数方差分布是合理的。

因此，Ljung-Box测试表明，预测误差中几乎没有自相关的证据，而预测误差的时间图和直方图表明，预测误差通常以均值零和常数方差分布是合理的。因此，我们可以得出结论，霍尔特的指数平滑为裙摆直径提供了足够的预测模型，这可能无法改进。此外，这意味着80％和95％预测区间所基于的假设可能是有效的。

Holt-Winters指数平滑

如果您有一个时间序列可以使用增加或减少趋势和季节性的加法模型来描述，您可以使用Holt-Winters指数平滑来进行短期预测。

Holt-Winters指数平滑估计当前时间点的水平，斜率和季节性分量。平滑由三个参数控制：α，β和γ，分别用于当前时间点的水平估计，趋势分量的斜率b和季节分量。参数alpha，beta和gamma都具有介于0和1之间的值，并且接近0的值意味着在对未来值进行预测时对最近的观察值的权重相对较小。

可以使用具有趋势和季节性的附加模型描述的时间序列的示例是澳大利亚昆士兰州的海滩度假小镇纪念品商店的月销售日志的时间序列（如上所述）：

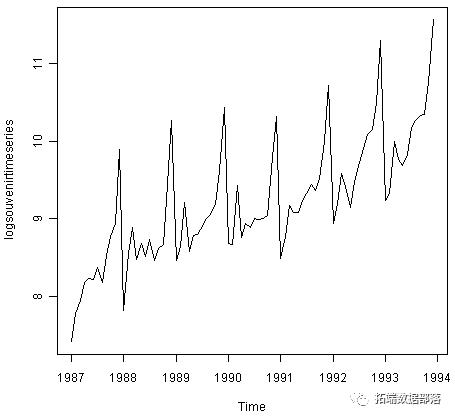
为了进行预测，我们可以使用HoltWinters（）函数拟合预测模型。例如，为了适应纪念品商店每月销售日志的预测模型，我们输入：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> logsouvenirtimeseries <- log(souvenirtimeseries)> souvenirtimeseriesforecasts <- HoltWinters(logsouvenirtimeseries)> souvenirtimeseriesforecastsHolt-Winters exponential smoothing with trend and additive seasonal component.Smoothing parameters:alpha: 0.413418beta : 0gamma: 0.9561275Coefficients:[,1]a 10.37661961b 0.02996319s1 -0.80952063s2 -0.60576477s3 0.01103238s4 -0.24160551s5 -0.35933517s6 -0.18076683s7 0.07788605s8 0.10147055s9 0.09649353s10 0.05197826s11 0.41793637s12 1.18088423> souvenirtimeseriesforecasts$SSE2.011491
 
    
 
  

α，β和γ的估计值分别为0.41,0.00和0.96。α（0.41）的值相对较低，表明当前时间点的水平估计是基于最近的观察和更远的过去的一些观察。β的值为0.00，表示趋势分量的斜率b的估计值不在时间序列上更新，而是设置为等于其初始值。这具有良好的直观感，因为水平在时间序列上发生了相当大的变化，但趋势分量的斜率b保持大致相同。相反，伽马值（0.96）很高，表明当前时间点的季节性成分估计仅基于最近的观察。

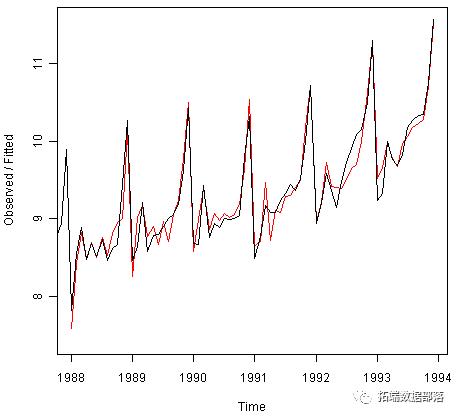
对于简单的指数平滑和Holt的指数平滑，我们可以将原始时间序列绘制为黑色线条，预测值为红线，顶部为：

> plot(souvenirtimeseriesforecasts)

我们从图中看到，Holt-Winters指数法非常成功地预测了季节性峰值，这种峰值大致发生在每年的11月。

为了对未包含在原始时间序列中的未来时间进行预测，我们在“预测”包中使用“forecast.HoltWinters（）”函数。例如，纪念品销售的原始数据是从1987年1月到1993年12月。如果我们想要预测1994年1月至1998年12月（48个月以上），并绘制预测图，我们将输入：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
     
 
     
> souvenirtimeseriesforecasts2 <- forecast.HoltWinters(souvenirtimeseriesforecasts, h=48)> plot.forecast(souvenirtimeseriesforecasts2)
 
    
 
  

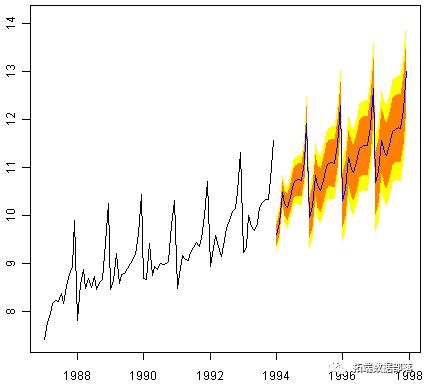
预测显示为蓝线，橙色和黄色阴影区域分别显示80％和95％的预测间隔。

我们可以通过检查样本内预测误差是否在滞后1-20处显示非零自相关，通过制作相关图并执行Ljung-Box测试来研究是否可以改进预测模型：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> acf(souvenirtimeseriesforecasts2$residuals, lag.max=20)> Box.test(souvenirtimeseriesforecasts2$residuals, lag=20, type="Ljung-Box")Box-Ljung testdata: souvenirtimeseriesforecasts2$residualsX-squared = 17.5304, df = 20, p-value = 0.6183
 
    
 
  

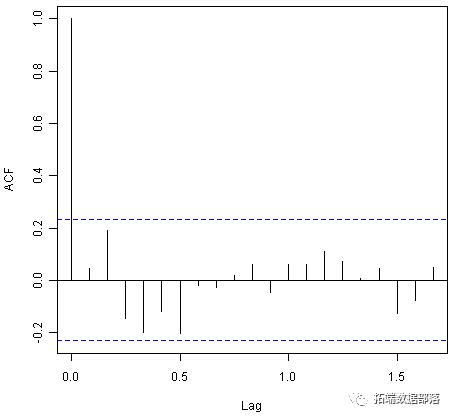
相关图表明，样本内预测误差的自相关不超过滞后1-20的显着性界限。此外，Ljung-Box检验的p值为0.6，表明在滞后1-20处几乎没有证据表明存在非零自相关。

我们可以通过制作预测误差和直方图（具有重叠的正常曲线）的时间图来检查预测误差是否随时间具有恒定的方差，并且通常以均值0分布：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
     
 
     
> plot.ts(souvenirtimeseriesforecasts2$residuals) # make a time plot> plotForecastErrors(souvenirtimeseriesforecasts2$residuals) # make a histogram
 
    
 
  

 

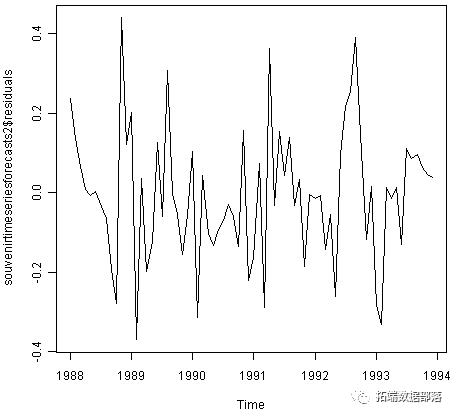
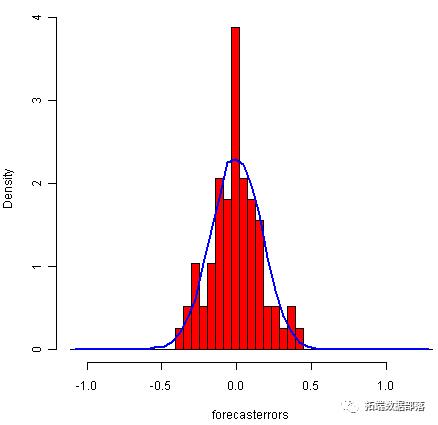
从时间图中可以看出，预测误差随时间变化具有恒定的变化。根据预测误差的直方图，预测误差通常以均值零分布似乎是合理的。

因此，对于预测误差，几乎没有证据表明在滞后1-20处存在自相关，并且预测误差似乎正态分布，均值为零，且随时间变化恒定。这表明Holt-Winters指数平滑提供了纪念品商店销售记录的充分预测模型，这可能无法改进。此外，预测区间所基于的假设可能是有效的。

ARIMA模型

指数平滑方法对于进行预测是有用的，并且不对时间序列的连续值之间的相关性做出假设。但是，如果要对使用指数平滑方法进行的预测进行预测间隔，则预测间隔要求预测误差不相关，并且通常以均值零和常数方差分布。

虽然指数平滑方法不对时间序列的连续值之间的相关性做出任何假设，但在某些情况下，您可以通过考虑数据中的相关性来建立更好的预测模型。自回归整合移动平均（ARIMA）模型包括时间序列的不规则分量的显式统计模型，其允许不规则分量中的非零自相关。

区分时间序列

ARIMA模型定义为固定时间序列。因此，如果您从一个非平稳的时间序列开始，您将首先需要“区分”时间序列，直到您获得一个固定的时间序列。如果你必须将时间序列d次除以获得一个固定序列，那么你有一个ARIMA（p，d，q）模型，其中d是差分的使用顺序。

你可以使用R中的“diff（）”函数来区分时间序列。例如，从1866年到1911年，女性裙子在1866年到1911年的年直径的时间序列并不是平稳的，因为水平变化很大随着时间的推移：

我们可以将时间序列（我们存储在“裙子系列”中，见上文）区分一次，并通过输入以下内容绘制差异系列：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
     
 
     
> skirtsseriesdiff1 <- diff(skirtsseries, differences=1)> plot.ts(skirtsseriesdiff1)
 
    
 
  

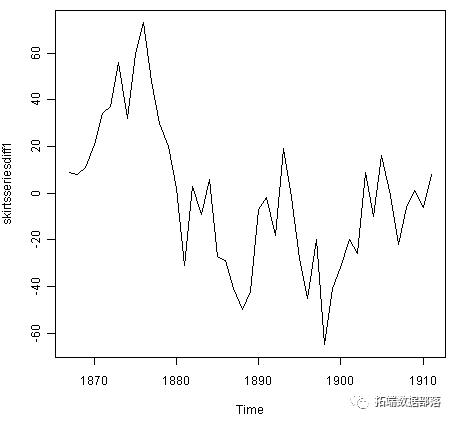
由此产生的第一个差异的时间序列（上图）似乎并不是平稳的。因此，我们可以将时间序列区分两次，看看是否为我们提供了一个固定的时间序列：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
     
 
     
> skirtsseriesdiff2 <- diff(skirtsseries, differences=2)> plot.ts(skirtsseriesdiff2)
 
    
 
  

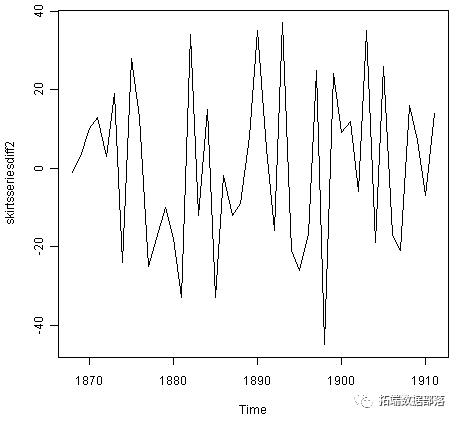
平稳性的测试

fUnitRoots包中提供了称为“单位根测试”的平稳性的正式测试，可在CRAN上获得，但这里不再讨论。

第二个差异的时间序列（上图）在均值和方差中似乎是平稳的，因为序列的水平随时间保持大致恒定，并且序列的方差随时间显得大致恒定。因此，似乎我们需要将裙子直径的时间序列区分两次以实现固定系列。

如果您需要将原始时间序列数据区分d次以获得固定时间序列，这意味着您可以为时间序列使用ARIMA（p，d，q）模型，其中d是使用差分的顺序。例如，对于女性裙子直径的时间序列，我们必须将时间序列区分两次，因此差异（d）的顺序为2.这意味着您可以使用ARIMA（p，2，q）你的时间序列的模型。下一步是计算ARIMA模型的p和q值。

另一个例子是英格兰历代国王的死亡时间序列（见上文）：

从时间图（上图），我们可以看出时间序列不是平均值。要计算第一个差异的时间序列并绘制它，我们键入：

  
    
    
  
 
   
> kingtimeseriesdiff1 <- diff(kingstimeseries, differences=1)
 
   
> plot.ts(kingtimeseriesdiff1)
 
  

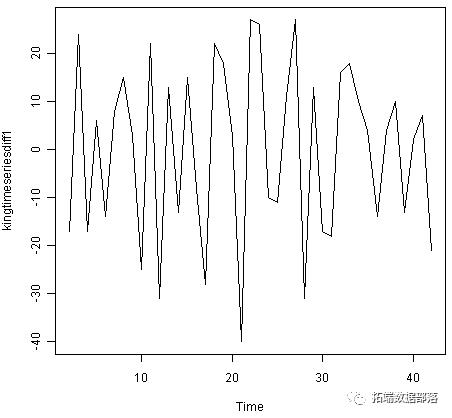
第一个差异的时间序列在均值和方差上似乎是固定的，因此ARIMA（p，1，q）模型可能适合于英格兰国王的死亡年龄的时间序列。通过采用第一个差异的时间序列，我们删除了国王死亡时代的时间序列的趋势分量，并留下不规则的成分。我们现在可以检查这个不规则分量的连续项之间是否存在相关性; 如果是这样，这可以帮助我们为国王死亡的年龄做出预测模型。

选择候选ARIMA模型

如果您的时间序列是静止的，或者您通过差分d次将其转换为静止时间序列，则下一步是选择适当的ARIMA模型，这意味着为ARIMA找到最合适的p和q值的值（p，d，q）模型。为此，您通常需要检查静止时间序列的相关图和部分相关图。

要绘制相关图和部分相关图，我们可以分别使用R中的“acf（）”和“pacf（）”函数。为了获得自相关和部分自相关的实际值，我们在“acf（）”和“pacf（）”函数中设置“plot = FALSE”。

英国国王死亡的例子

例如，为了绘制英格兰国王死亡时间的一次差异时间序列的滞后1-20的相关图，并获得自相关的值，我们输入：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> acf(kingtimeseriesdiff1, lag.max=20) # plot a correlogram> acf(kingtimeseriesdiff1, lag.max=20, plot=FALSE) # get the autocorrelation valuesAutocorrelations of series 'kingtimeseriesdiff1', by lag0 1 2 3 4 5 6 7 8 9 101.000 -0.360 -0.162 -0.050 0.227 -0.042 -0.181 0.095 0.064 -0.116 -0.07111 12 13 14 15 16 17 18 19 200.206 -0.017 -0.212 0.130 0.114 -0.009 -0.192 0.072 0.113 -0.093
 
    
 
  

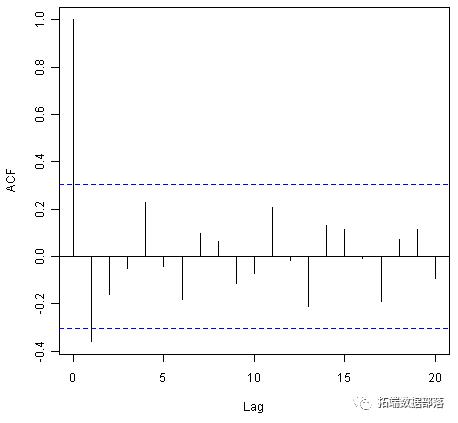
我们从相关图中看到，滞后1（-0.360）处的自相关超过了显着边界，但是滞后1-20之间的所有其他自相关都没有超过显着边界。

为了绘制英语国王死亡时间的一次差异时间序列的滞后1-20的部分相关图，并获得部分自相关的值，我们使用“pacf（）”函数，键入：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> pacf(kingtimeseriesdiff1, lag.max=20) # plot a partial correlogram> pacf(kingtimeseriesdiff1, lag.max=20, plot=FALSE) # get the partial autocorrelation valuesPartial autocorrelations of series 'kingtimeseriesdiff1', by lag1 2 3 4 5 6 7 8 9 10 11-0.360 -0.335 -0.321 0.005 0.025 -0.144 -0.022 -0.007 -0.143 -0.167 0.06512 13 14 15 16 17 18 19 200.034 -0.161 0.036 0.066 0.081 -0.005 -0.027 -0.006 -0.037
 
    
 
  

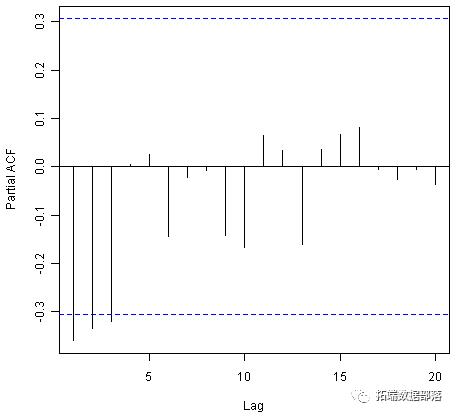
部分相关图显示滞后1,2和3的部分自相关超过显着边界，为负，并且随着滞后的增加而在幅度上缓慢下降（滞后1：-0.360，滞后2：-0.335，滞后3：-0.321 ）。在滞后3之后，部分自相关变为零。

由于在滞后1之后相关图为零，并且在滞后3之后部分相关图变为零，这意味着对于第一差异的时间序列，以下ARMA（自回归移动平均）模型是可能的：

• ARMA（3,0）模型，即阶数为p = 3的自回归模型，因为部分自相关图在滞后3之后为零，并且自相关图结束为零（尽管可能过于突然，因为该模型是合适的）

• 一个ARMA（0,1）模型，即q = 1的移动平均模型，因为自相关图在滞后1之后为零，而部分自相关图结束为零

• 一个ARMA（p，q）模型，即p和q大于0的混合模型，因为自相关图和部分相关图尾部为零（尽管相关图可能会突然变为零，因为该模型是合适的）

我们使用简约原理来确定哪个模型最好：也就是说，我们假设参数最少的模型是最好的。ARMA（3,0）模型具有3个参数，ARMA（0,1）模型具有1个参数，ARMA（p，q）模型具有至少2个参数。因此，ARMA（0,1）模型被认为是最佳模型。

ARMA（0,1）模型是阶数1或MA（1）模型的移动平均模型。这个模型可以写成：X_t - mu = Z_t - （theta * Z_t-1），其中X_t是我们正在研究的平稳时间序列（英国国王死亡时的第一个不同年龄系列），mu是平均值时间序列X_t，Z_t是具有平均零和恒定方差的白噪声，并且theta是可以估计的参数。

MA（移动平均）模型通常用于模拟时间序列，该时间序列显示连续观察之间的短期依赖性。直觉上，很有意义的是，MA模型可以用来描述英国国王死亡时间序列中的不规则成分，因为我们可以预期特定英国国王的死亡年龄对年龄有一定影响。在接下来的一两个国王的死亡，但对国王死亡的年龄影响不大，在那之后更长的统治时间。

 auto.arima（）函数

auto.arima（）函数可用于查找适当的ARIMA模型，例如，键入“library（forecast）”，然后键入“auto.arima（kings）”。输出说适当的模型是ARIMA（0,1,1）。

由于ARMA（0,1）模型（p = 0，q = 1）被认为是英国国王死亡年龄的第一个差异的时间序列的最佳候选模型，那么原始的时间序列死亡年龄可以使用ARIMA（0,1,1）模型建模（p = 0，d = 1，q = 1，其中d是所需差分的顺序）。

 

使用ARIMA模型进行预测

为时间序列数据选择最佳候选ARIMA（p，d，q）模型后，您可以估计该ARIMA模型的参数，并将其用作预测模型，以便对时间序列的未来值进行预测。

您可以使用R中的“arima（）”函数估计ARIMA（p，d，q）模型的参数。

英国国王死亡时代的例子

例如，我们在上面讨论过，ARIMA（0,1,1）模型似乎是英格兰国王死亡年龄的合理模型。您可以使用R中“arima（）”函数的“order”参数在ARIMA模型中指定p，d和q的值。使ARIMA（p，d，q）模型适合此时间序列（我们存储在变量“kingstimeseries”中，见上文），我们输入：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> kingstimeseriesarima <- arima(kingstimeseries, order=c(0,1,1)) # fit an ARIMA(0,1,1) model> kingstimeseriesarimaARIMA(0,1,1)Coefficients:ma1-0.7218s.e. 0.1208sigma^2 estimated as 230.4: log likelihood = -170.06AIC = 344.13 AICc = 344.44 BIC = 347.56
 
    
 
  

如上所述，如果我们将ARIMA（0,1,1）模型拟合到我们的时间序列，则意味着我们将ARMA（0,1）模型拟合到第一个差异的时间序列。可以写入ARMA（0,1）模型X_t-mu = Z_t - （theta * Z_t-1），其中theta是要估计的参数。根据“arima（）”R函数（上图）的输出，在拟合ARIMA（0,1,1）模型的情况下，theta的估计值（在R输出中给定为'ma1'）为-0.7218到国王死亡的时间序列。

指定预测间隔的置信度

您可以使用“level”参数在forecast.Arima（）中指定预测间隔的置信度。例如，要获得99.5％的预测间隔，我们将键入“forecast.Arima（kingstimeseriesarima，h = 5，level = c（99.5））”。

然后，我们可以使用ARIMA模型使用“预测”R包中的“forecast.Arima（）”函数对时间序列的未来值进行预测。例如，为了预测接下来的五位英国国王的死亡年龄，我们输入：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> library("forecast") # load the "forecast" R library> kingstimeseriesforecasts <- forecast.Arima(kingstimeseriesarima, h=5)> kingstimeseriesforecastsPoint Forecast Lo 80 Hi 80 Lo 95 Hi 9543 67.75063 48.29647 87.20479 37.99806 97.5031944 67.75063 47.55748 87.94377 36.86788 98.6333845 67.75063 46.84460 88.65665 35.77762 99.7236346 67.75063 46.15524 89.34601 34.72333 100.7779247 67.75063 45.48722 90.01404 33.70168 101.79958
 
    
 
  

英国国王的原始时间序列包括42位英国国王的死亡年龄。forecast.Arima（）函数给出了对接下来的五位英国国王（国王43-47）的死亡年龄的预测，以及这些预测的80％和95％预测区间。第42位英国国王的死亡年龄为56岁（我们的时间序列中最后一次观察到的值），ARIMA模型给出了接下来五位国王死亡的预测年龄为67.8岁。

我们可以使用我们的ARIMA（0,1,1）模型绘制前42个国王的死亡年龄，以及预测这42个国王和接下来的5个国王的年龄：

> plot.forecast(kingstimeseriesforecasts)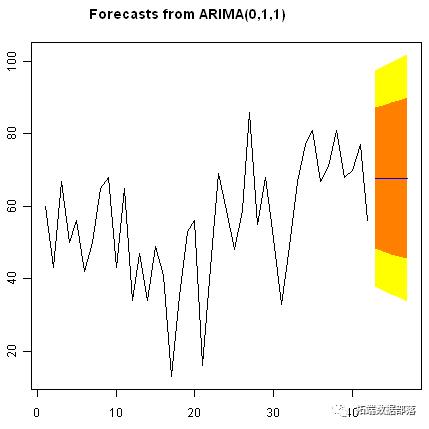

与指数平滑模型的情况一样，最好研究ARIMA模型的预测误差是否正态分布为均值为零和常数方差，以及是否为连续预测误差之间的相关性。

例如，我们可以为国王死亡时的ARIMA（0,1,1）模型制作预测误差的相关图，并通过键入以下内容执行Ljung-Box测试，即滞后1-20。

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
      
 
      
 
      
 
     
 
     
> acf(kingstimeseriesforecasts$residuals, lag.max=20)> Box.test(kingstimeseriesforecasts$residuals, lag=20, type="Ljung-Box")Box-Ljung testdata: kingstimeseriesforecasts$residualsX-squared = 13.5844, df = 20, p-value = 0.851
 
    
 
  

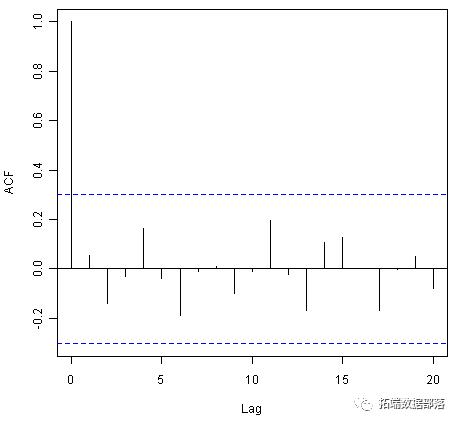
由于相关图显示滞后1-20的样本自相关都不超过显着性边界，并且Ljung-Box检验的p值为0.9，我们可以得出结论，很少有证据证明非零自相关预测错误在滞后1-20。

为了研究预测误差是否正态分布为均值为零和常数方差，我们可以制作预测误差的时间图和直方图（带有重叠的正态曲线）：

  
    
    
  
 
   
 
    
 
     
 
      
 
      
 
     
 
     
> plot.ts(kingstimeseriesforecasts$residuals) # make time plot of forecast errors> plotForecastErrors(kingstimeseriesforecasts$residuals) # make a histogram
 
    
 
  

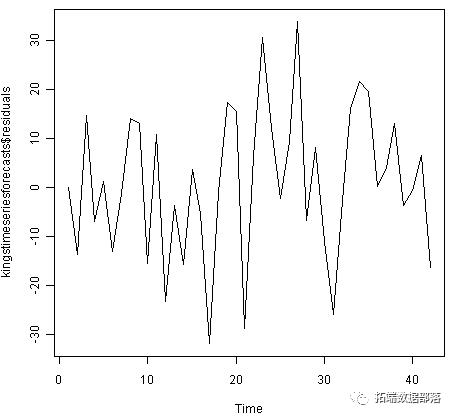
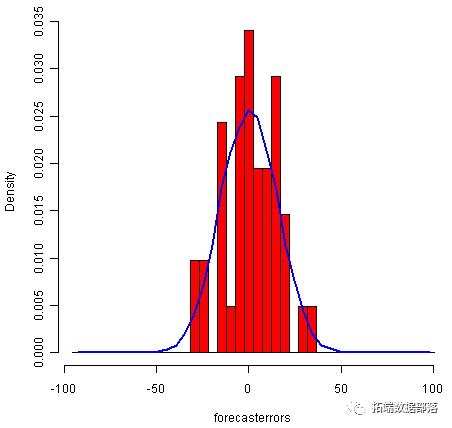
样本内预测误差的时间图表明，预测误差的方差似乎随着时间的推移大致不变（尽管时间序列的后半部分的方差可能略高）。时间序列的直方图显示预测误差大致正态分布，均值似乎接近于零。因此，预测误差通常以均值零和常数方差分布是合理的。

由于连续的预测误差似乎没有相关性，并且预测误差似乎正常分布为均值为零且方差不变，因此ARIMA（0,1,1）似乎确实为死亡年龄提供了充分的预测模型。 

 

点击标题查阅往期内容

更多内容，请点击左下角“阅读原文”查看

案例精选、技术干货 第一时间与您分享

长按二维码加关注

更多内容，请点击左下角“阅读原文”查看