R语言 | 一般加性模型的简介应用举例及R语言操作

Posted 2021-04-18 生物空间站

一般加性模型的简介、应用及R语言操作举例

前文在“ ”中，提到当未知自变量和响应变量间的关系，难以选择合适的参数模型描述二者间的响应状态，或者期望探索二者可能的响应曲线形式时，非参数的平滑回归是一种合理而有效的选择。局部加权回归（locally weighted regression，LOESS）和加性模型（additive model）是常见的两种非参数平滑回归，在前文“ ”中均作了简单提及。LOESS回归相对简单就不再多说，但前文并未对加性模型作过多描述，因此本篇对加性模型作个简介。

加性模型可描述为多元回归的非参数化平滑回归形式。类似 和 的关系，加性模型也常见两种形式，一般加性模型（general additive model）和广义加性模型（generalized additive model，GAM）。类似地，一般加性模型简单易懂，假定响应变量大致服从正态分布时使用；而广义加性模型则主要是一类服务于一组来自 （如正态分布、泊松分布、二项分布、负二项分布、指数分布等）的响应变量的框架，一般加性模型也可视为广义加性模型的某种形式。

本篇首先对一般加性模型作个简介，并在下文中统一使用“加性模型”一词。有关 广义加性模型的内容放在下节讨论。

一般加性模型的简介

  

加性模型是常被用来探索响应变量与自变量之间函数形式的一种较为灵活的工具。在一般加性模型中，假定响应变量服从正态分布，并试图建立自变量与响应变量条件均值的非参数函数的可能形式。

一般加性模型的定义

对于参数回归模型而言，响应变量与自变量之间的关系通常可具化为特定的函数公式来体现。

例如在最常见的中，响应变量Y的条件均值与自变量X之间的函数关系为线性且描述为简单加权和形式：

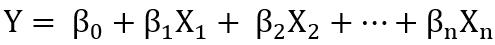
多元线性回归假定响应变量Y服从正态分布，式中β₁-β_n代表了自变量X₁-X_n的回归系数（斜率），β₀是截距，+体现了响应变量Y的条件均值是自变量的简单加权和。回归的目的是找到一组最优的模型参数（斜率和截距值的组合），使响应变量Y的观测值和预测值（条件均值）之间的残差平方和最小化。

 

与上述这种常见的参数回归相比，在非参数化的加性模型中，只设定了可加和性，而并没有对变量关系的函数形式作出假设。

以一般加性模型为例，假定响应变量Y服从正态分布，自变量X和响应变量Y的条件均值之间的关系可简单表示为：

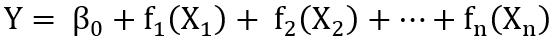
式中f_n(.)是未指明的函数，需要非参数式地予以估计，“非参数”一词反映了函数f_n(.)不是用参数来定义的。总的来说，加性模型放宽了对响应关系加和形式的限制，允许任意函数之和来建模结果，自变量和响应变量之间的关系可以为任意线性或非线性。

一般加性模型的表现形式

如上所述，由于f_n(.)是非参数的函数，因此在加性模型中，变量间关系通常无法通过简单的数学公式（如线性回归中简单的y=ax+b这种）来描述。此时对于响应变量和自变量关系的理解，可以以平滑曲线的图形的方式表达二者间的依赖性。此外，图形化的展示方式还可帮助对可能有效替代的参数模型作出假设。

接下来就通过在R语言中运行加性模型，在过程中加深理解。

R包mgcv执行一般加性模型的简单示例

  

在R中，可用于实现加性模型的R包很多，其中mgcv包是执行加性模型的最常见R包之一，函数gam()提供了对一般加性模型和广义加性模型的通用方法。在下文，就以mgcv包中方法为例，展示一般加性模型在R语言中的实现。

示例数据集

R包agridat中的内置数据集lasrosas.corn，记录了不同氮肥处理下的阿根廷玉米田的产量监测数据，以及地理环境等条件。

#示例数据集，详情加载 agridat 包后 ?lasrosas.corn
library(agridat)
 
data(lasrosas.corn)
head(lasrosas.corn)

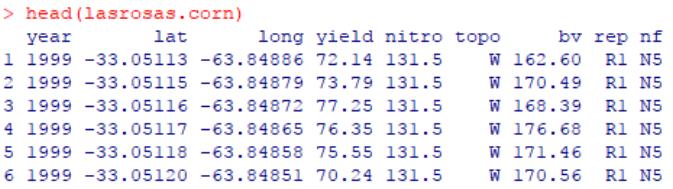
该数据集共计包含8列变量的3443行观测值。

year，1999年或2001年的观测数据；

lat和long，分别为玉米田所处的纬度和经度；

yield，产量（quintals/ha）；

nitro，氮肥浓度（kg / ha）；

topo，地形因子，代表了不同地区的玉米田；

bv，亮度值，帮助文档中提到该值越高代表土壤有机物含量更低；

rep，试验中的生物学重复；

nf，氮浓度梯度，根据施加的氮肥浓度（nitro）记录为N0-N5。

单变量分析示例

首先来看一个简单的单变量情形，帮助理解加性模型的实现过程和对结果的解读。

现在期望探索玉米产量（yield）与施加氮肥浓度（nitro）的关系：随着氮肥施加水平的提升，是否能够使玉米增产，或者这种增产效应体现为怎样的模式。由于二者的关系可能并非线性响应这样简单，并且也不容易联想二者其它可能的响应状态，因此不妨首先通过平滑回归来对二者可能的关系作个探索。如前文“”所述，可使用LOESS回归或加性模型执行平滑拟合。在本示例中，假定响应变量服从正态分布，使用一般加性模型执行平滑回归。

mgcv包中执行加性模型的函数是gam()，默认情况下其执行一般加性模型。gam()拟合变量时，对于各自变量需要设置平滑器类型，以拟合响应变量和自变量的局部平滑，例如s()将平滑器指定为样条平滑，lo()将平滑器指定为LOESS平滑等。在下文示例中统一使用样条平滑来实现。

library(mgcv)
 
#避免多年度、多地区间数据混乱，选取 1999 年的 W 地区玉米田的数据为例进行后续分析
lasrosas.corn.select <- subset(lasrosas.corn, year == 1999 & topo == 'W')
 
#此处以一般加性模型为例，拟合玉米产量与施加氮肥浓度的平滑回归
#需要在 gam() 函数中指定自变量的局部平滑器类型，如 s() 的样条平滑、lo() 的 LOESS 平滑等
#详情 ?gam、?s、?lo 等
 
#以样条平滑为例，实现响应变量与自变量的局部平滑拟合
#s() 中，参数 k 可用于指定平滑程度，值越小约趋于线性平滑，越高扭动越厉害，参考以下示例
fit1_k3 <- gam(yield~s(nitro, k = 3), data = lasrosas.corn.select)
summary(fit1_k3)  #检验自变量的显著性以及评估回归整体的方差解释率
 
fit1_k5 <- gam(yield~s(nitro, k = 5), data = lasrosas.corn.select)
summary(fit1_k5)  #检验自变量的显著性以及评估回归整体的方差解释率
 
fit1_k6 <- gam(yield~s(nitro, k = 6), data = lasrosas.corn.select)
summary(fit1_k6)  #检验自变量的显著性以及评估回归整体的方差解释率
 
#平滑回归曲线图，默认显示 95% 置信区间
par(mfrow = c(2, 3))
plot(fit1_k3)
plot(fit1_k5)
plot(fit1_k6)
plot(fit1_k3, select = 1, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)
plot(fit1_k5, select = 1, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)
plot(fit1_k6, select = 1, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)

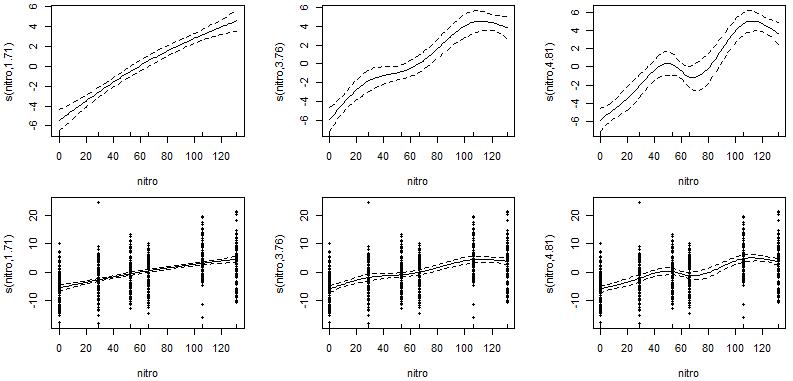
一定要注意，样条平滑函数s(k=?)中平滑参数值的选择会强烈影响结果，有时候不同输出会导致不同的解释。在LOESS平滑函数lo(span=?)中也同样如此。

例如在这个示例中，分别拟合了3种不同平滑程度的回归，根据曲线图可看到，3种平滑回归结果下的玉米产量与施加氮肥浓度呈现不同状态的响应。第1种（s()平滑参数k=3，左图）显示玉米产量随施加氮肥浓度的提升而平稳增加；第2种（s()平滑参数k=5，中图）显示，低中浓度的氮肥下玉米产量随施加氮肥浓度的提升而增加，但高浓度氮肥似乎会产生胁迫抑制产量；第3种（s()平滑参数k=6，右图）则呈现无规律状态。

实际的生物学意义解读中，只允许一种正确的解释，因此解释不同参数的平滑回归输出时必须谨慎。拟合出的响应曲线必须结合实际情况判断，任何与当前研究对象的理解存在矛盾的地方都必须进行检查。再回到上示例，第3种无规则状态肯定不能选择；对于第1或第2种，需要根据实际经验选择最符合实际情况的那个（所以，有些东西光有统计学理论，而欠缺生物学背景，也是不行的）。

此外，对于加性模型这种非参数平滑回归而言，大都当作探索性工具来使用，辅助对潜在的变量关系提出假设。对于上述情况1或2，如果最后选择情形1，则表明玉米产量随施加氮肥浓度的提升而逐渐增加，后续就不妨简化为这种参数模型进行描述；如果最后选择情形2，则表明玉米产量在低中浓度和浓度氮肥下可能表现为不同趋势的响应，不妨尝试寻找突出氮肥梯度的拐点。

 

尽管加性模型作为非参数平滑回归的一种类型，常作为探索性工具来使用，但在R语言中仍提供了对自变量的显著性、方差解释率等进行统计的方法。以上述某个结果为例展示。

#检验自变量的显著性以及评估回归整体的方差解释率
summary(fit1_k5)

结果显示氮肥浓度对玉米产量的影响是显著的。但是这个回归的整体解释率21.7%，算不上很高，可能归因于原数据太过离散，如上文曲线图中显示的产量分布所示的那样。

平滑参数的选择也会强烈影响解释率。理论上，曲线越平滑趋于直线，R²越低；曲线扭动越曲折，R²越高。但如上文所展示的那样，曲线往往不能太曲折，否则影响生物学意义解读。

其它情况，除了氮肥浓度外，其它因素如土壤中有机物含量等也会存在不可忽视的影响。接下来，讨论多变量的回归。

多变量分析示例

现在期望探索施加氮肥浓度、土壤有机物含量对玉米产量的综合影响，此时考虑执行一个二元回归。类似上文过程，不妨首先通过一般加性模型的平滑回归来对多变量响应关系作个探索。

 

同上文所述，gam()拟合变量时，对于各自变量需要设置平滑器类型，以拟合响应变量和自变量的局部平滑，例如s()将平滑器指定为样条平滑，lo()将平滑器指定为LOESS平滑等。在下文示例中统一使用样条平滑来实现。

#类似多元回归方法，以 + 相连各自变量，表示加和效应，详情 ?gam
#对于各自变量，都需要指定局部平滑器类型，如这里统一为 s() 的样条平滑，详情 ?s()
#各自变量允许设置各自不同的平滑参数，如下示例
fit2_k3_k5 <- gam(yield~s(nitro, k = 3) + s(bv, k = 5), data = lasrosas.corn.select)
summary(fit2_k3_k5)  #检验自变量的显著性以及评估回归整体的方差解释率
 
fit2_k5_k10 <- gam(yield~s(nitro, k = 5) + s(bv, k = 10), data = lasrosas.corn.select)
summary(fit2_k5_k10)  #检验自变量的显著性以及评估回归整体的方差解释率
 
#平滑回归曲线图，默认显示 95% 置信区间
#多变量时，通过 select 选择第 n 个自变量展示和响应变量的回归曲线
par(mfrow = c(2, 2))
plot(fit2_k3_k5, select = 1, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)
plot(fit2_k3_k5, select = 2, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)
plot(fit2_k5_k10, select = 1, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)
plot(fit2_k5_k10, select = 2, pch = 20, se = TRUE, rug = TRUE, residuals = TRUE)

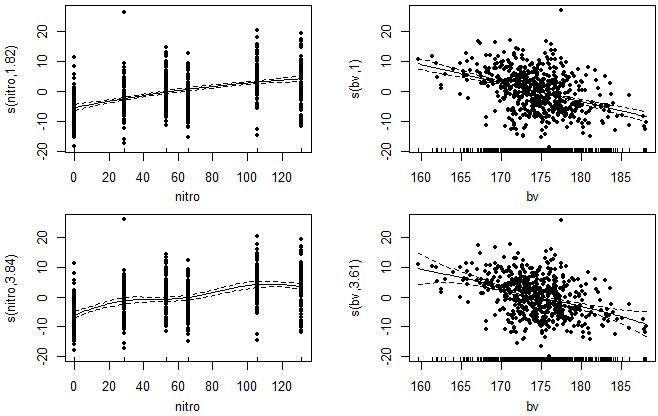
同上文，平滑参数值的选择会强烈影响结果，有时候不同输出会导致不同的解释，因此平滑参数值的选择需谨慎。多变量的情况中，最好在事先分别对每个变量拟合回归，结合实际情况考察生物学意义有效的平滑曲线程度的选择，并将它代入之多变量回归中。

例如在这个示例中，分别拟合了2种不同平滑程度的回归，上下两图分别展示。整体趋势上，玉米产量随施加氮肥浓度的增加而提升，但不同平滑程度的选择影响了局部趋势的解释，特别是在低中浓度氮向高浓度氮转变时对玉米产量的效应，这和上文的单变量分析的结论大致相似。曲线图趋势上来看，土壤有机物含量对玉米产量的影响也很明显，由于数据集的帮助文档中提到bv值与土壤有机物含量为负相关关系，而产量（yield）与bv值呈现负相关，因此可知更高的土壤有机物含量同样有助于玉米产量的提升。

此外还需注意，尽管平滑曲线图显示yield 和bv之间似乎是线性的，更改局部平滑器函数s()中平滑参数k的值后的曲线也未发生较大程度改变，但结合图中变量数值的分布特征，也不难看出这是由于响应变量在自变量某区段内过于集中产生的“伪线性”现象。实际中仍存在较大的离散度，应当谨慎对待。

#拓展作图，二元平滑回归的二维平面等高线图和三维图，详情 ?vis.gam
#二维平面等高线图其实就是三维图中 z 轴的降维投影形式
par(mfrow = c(2, 2))
 
vis.gam(fit2_k3_k5, color = 'cm', plot.type = 'contour')
points(lasrosas.corn.select$nitro, lasrosas.corn.select$bv, pch = 16)
vis.gam(fit2_k5_k10, color = 'cm', plot.type = 'contour')
points(lasrosas.corn.select$nitro, lasrosas.corn.select$bv, pch = 16)
vis.gam(fit2_k3_k5, color = 'cm', theta = 30)
vis.gam(fit2_k5_k10, color = 'cm', theta = 30)

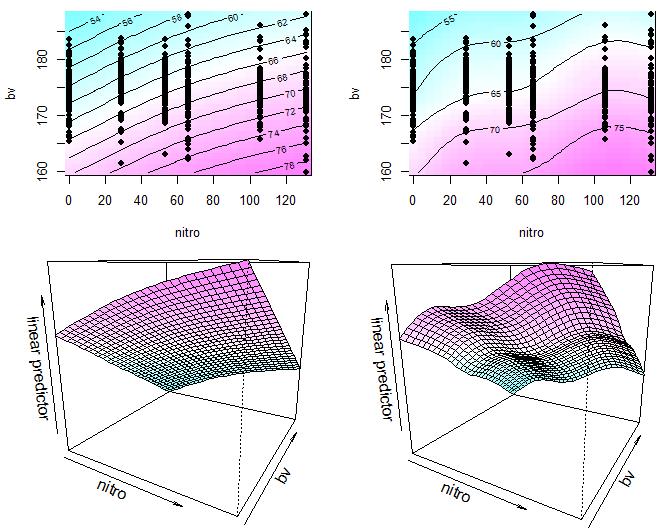
关于ggplot2实现等高线图绘制的方法，可参考前文“”。

 

上述只是通过曲线图大致描述了趋势，您仍可以通过summary()评估回归中变量的显著性，以及比较前后两个回归的方差解释率。以上述某个结果为例展示。

#检验自变量的显著性以及评估回归整体的方差解释率
summary(fit2_k5_k10)

通过R内置的统计方法评估变量的显著性，显示氮肥浓度、土壤有机物含量对玉米产量的影响都是显著的。同时比较前后两个回归的方差解释率，与上文单变量回归中只考虑氮肥浓度相比（R²=0.217），加入土壤有机物含量的二元回归的R²=0.344（展示的这个回归示例中氮浓度的平滑参数和上文单变量回归中保持了一致，便于比较），即环境因素对作物产量的解释率得到有效提升。

考虑交互效应的示例

在常规形式的参数多元回归中，如果考虑变量间的交互效应，使用“*”、“:”等代替“+”连接自变量，执行。而在非参数的加性模型中，如果考虑交互效应，则需要将交互项指定在平滑器函数中，参考以下示例。

#在上文的氮肥浓度、土壤有机物含量对玉米产量影响的二元回归的基础上
#继续考虑加入氮肥浓度和土壤有机物含量的交互效应
 
#直接在同一个平滑器内部输入所考虑交互效应的两自变量
#本示例使用样条平滑 s()，此时两自变量需统一设置平滑参数
fit2_inter <- gam(yield~s(nitro, bv, k = 5), data = lasrosas.corn.select)
summary(fit2_inter)
 
#二维平面等高线图和三维图，详情 ?vis.gam
par(mfrow = c(1, 2))
vis.gam(fit2_inter, color = 'cm', plot.type = 'contour')
points(lasrosas.corn.select$nitro, lasrosas.corn.select$bv, pch = 16)
vis.gam(fit2_inter, color = 'cm', theta = 30)

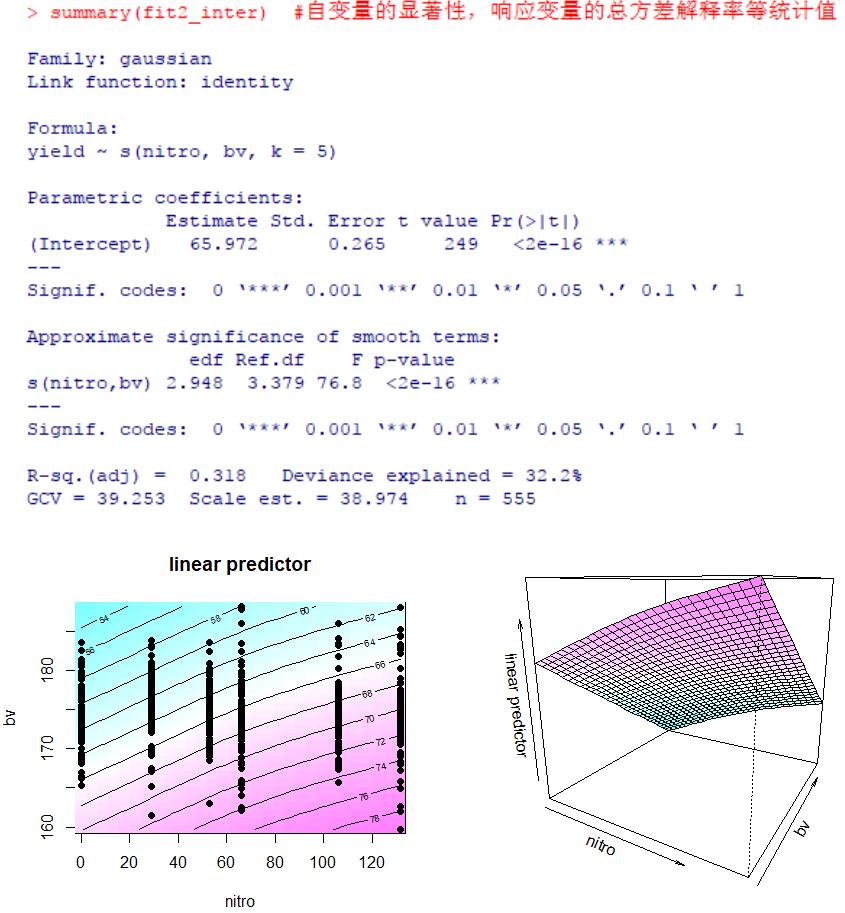
如果您好奇为何这里加入交互效应后，相比上述不带交互项的回归R²降低了，是因为这里平滑参数的值调低了所致。这里在样条平滑函数s()中，bv的平滑参数k=5，而上文展示的回归中bv的平滑参数k=10，二者最好就不要在一起比较了，因为这类情形中拟合曲线所描述的响应状态的生物学解释更重要，模型的方差解释率反而其次。如上文所述，平滑参数的选择会强烈影响解释率，曲线越平滑趋于直线R²越低；曲线扭动越曲折R²越高，但曲线往往不能太曲折，否则影响生物学意义解读。

       

关于加性模型的其它问题

  

尽管非参数平滑回归中不存在固定模式的变量关系的函数形式，但它提供了更大的灵活性用于寻求可能的变量间响应关系。因此，类似大多数探索性的工具，加性模型同样具有很高的应用价值。例如环境和生态学相关文献中经常拟合加性模型作为最终模型来展示，而不做过多的批判性评价。但最关键的一点是，如何选择最合适的平滑参数值，使变量间关系贴合实际并值得被解释。这使得加性模型的结果需要用科学知识或一般常识小心检查和解释，然后才能提出和检验关于模型的假设，否则可能会产生存在矛盾解释的模型。

最后展示一篇文献中使用加性模型分析生物学问题的案例，帮助加深对它使用的理解。

    

文献中使用加性模型探索生物响应问题的一个实例

  

物种性状特征常用于诊断和预测其对长期气候变化的响应，但较少研究探索对极端气候事件（例如长期干旱）的特征敏感性。Aspin 等（2019）通过模拟河流枯竭试验，在不断加剧的干旱梯度（包括生境丧失的几个关键阶段）中对底栖大型无脊椎动物群落性状特征的响应趋势进行了测试。多种响应阈值的检测表明，干旱强度的较小扰动就足以引起河流群落性状的较大非线性响应变化，某些性状可能是物种或群落对极端环境干扰抗性的有价值的功能性生物标记，以及提到基于特征的方法对于诊断对全球变化的灾难性生态响应特别有用。

在文中部分章节里，作者使用加性模型分析了群落性状特征对干旱环境的响应过程。因此接下来节选这部分内容，帮助大家理解加性模型的使用。

中宇宙模拟河流干旱试验

作者通过中宇宙试验模拟河流生态系统，以期望最大程度地反映河流栖息地的物理化学和生物学真实性。在试验前期阶段，各中宇宙以相同的条件运转，使生态环境达到近似的稳定状态。随后的时间里，通过对各中宇宙施加不同梯度的干旱处理，模拟河流栖息地逐渐干枯的生境扰动或破坏模式，并监测环境水量、水域面积、水温、溶解氧等环境指标，综合环境指标的测量值定义各中宇宙站点所处的干旱强度。

原文图S1，中宇宙试验，显示了模拟的河流生态系统受到不同干旱扰动的梯度变化。

干旱强度（drought intensity，DI）分配为[0,1]区间内的数值指代，0代表无干旱干扰，1表示严重缺水。DI<0.2（左一、二）是温度稳定、水流量相对较高的水域环境，底栖生境损失最小；0.2<DI<0.7（中，右二）代表中强度的干旱扰动，表现为浅滩干燥和局部孤立的水池，平均湿润面积损失一半且温度变化更大，流量可忽略；DI> 0.7（右一）为枯竭的河床，95％以上的湿润区域损失并伴有极端的温度不稳定。

河流底栖大型无脊椎动物群落的性状特征测量

取样时在底栖生境中收集约3cm深度的河床样本，后续借助显微镜等工具观察并鉴定样本中可识别的大型无脊椎动物的性状特征，以及对物种个体密度进行计数。而对于肉眼难以识别解析的物种性状特征，则使用欧洲性状数据库中在属水平上分配的平均特征谱代替。

共选择了16种性状特征用作测量记录，涉及体型尺寸、繁殖方式、环境适应性、扩散迁徙能力、呼吸方式、饮食习惯等。最后结合物种性状特观测量值以及各物种的丰度数据，计算河流底栖群落整体的丰度加权平均性状特征，并标准化到(0,1)数值区间以消除不同特征的权重差异。

群落性状特征对河流干旱的响应分析

随后分析在不断加剧的干旱梯度（包括生境丧失的几个关键阶段）中，底栖大型无脊椎动物群落性状特征的响应趋势。

由于不同的群落功能性状对环境干旱加剧既存在线性又存在非线性的响应，对参数回归模型的选择产生困难，因此作者选择加性模型来建模响应曲线，并根据拟合曲线的斜率变化检测干旱期间的功能阈值（作者从统计学意义上使用了阈值一词，代指响应关系中响应变量的变化比自变量变化更快的一个阶段，统计上可靠的生态阈值检测方法通常用于评估生态系统中栖息地扰动的最大承受水平）。

 

单变量加性模型的平滑回归结果显示，16种群落性状特征响应干旱加剧的趋势可分为3类。

Type N（N型响应）不受干旱影响，它们主要是生物的固有生理结构特征，如多化性、卵胎生等。

Type L（L型响应）沿干旱梯度呈现稳定增加或减小，它们主要涉及生物的迁移扩散能力、运动方式、穴居、饮食习惯等行为属性。随着干旱加剧伴随的水域栖息地减少以及河床浅滩的暴露，活跃的空中扩散、挖穴和多能性取食变得越来越普遍，有翅类群（如双翅目昆虫）数量增加，而水生扩散和爬行类群（如扁虫）相应减少。

Type T（T型响应）在低中等干旱强度下变化很小或没有变化，但在较高干旱强度下剧烈改变，沿干旱梯度存在明显的断点（生态响应阈值）。它们主要涉及生物的体型、呼吸方式、嗜热性、冷适应和抗旱性等形态或生理特征。随着干旱加剧，群落趋向小体型（大多数双翅目的特征）、宽温度耐受性和高抗旱性物种转变，同时大体型、皮肤呼吸（很多水生动物的标志）和冷适应物种比重降低。

总的来说，这些响应趋势描述了河流底栖大型无脊椎动物群落的行为（分散、运动、进食等）对河流栖息地的中等强度干旱敏感，而高强度的河床干燥主要对群落种群形态和生理变化（体型大小、呼吸、环境适应性等）存在最强烈选择。干旱导致的生态位转变触发了某些功能群体的种群崩溃，特别是某些非飞行类群逐渐被飞行类群取代。重要性状特征响应突出了极端干旱对河流群落功能的潜在普遍影响。

原文图1，干旱强度（drought intensity，DI）对16种群落性状特征的影响和选择。变量间关系用加性模型进行拟合，虚线为95％置信区间。

       

参考资料

  

https://www.r-bloggers.com/generalized-addictive-models-and-mixed-effects-in-agriculture/

钱松. 环境与生态统计:R语言的应用（曾思育 译）. 高等教育出版社, 2011.

Aspin T W, Khamis K, Matthews T J, et al. Extreme drought pushes stream invertebrate communities over functional thresholds. Global Change Biology, 2019, 25(1): 230-244.

我就知道你在看