笔记 选择排序
Posted 小宏成长记
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了笔记 选择排序相关的知识,希望对你有一定的参考价值。
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
一、内存的工作原理
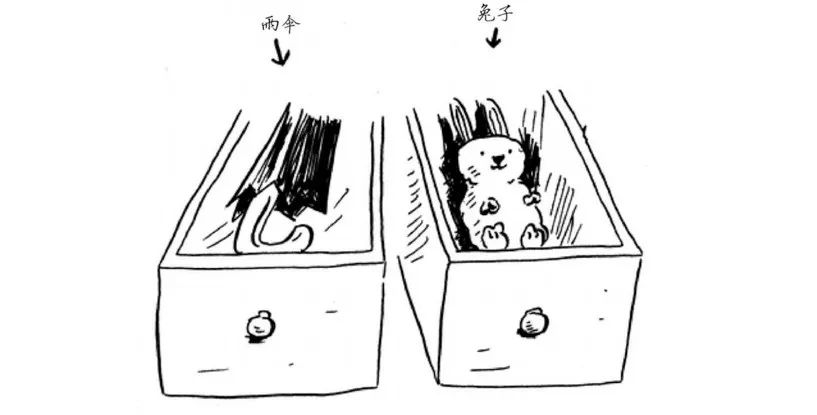
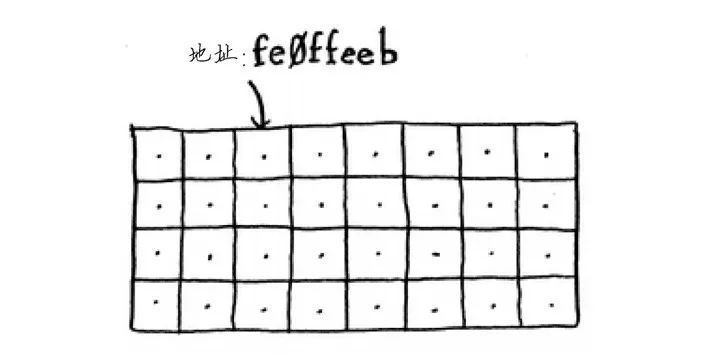
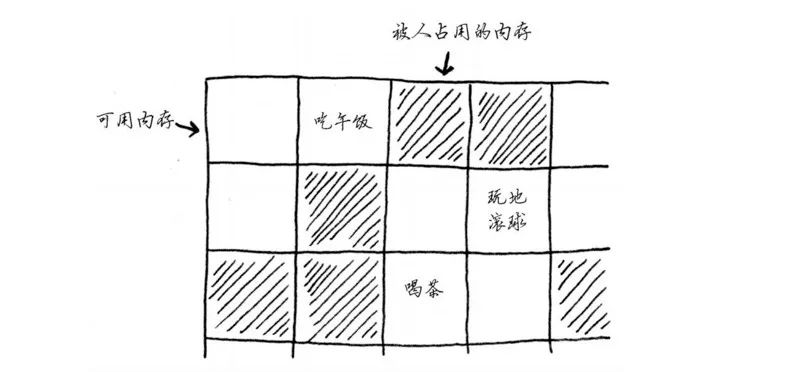
假设你去看演出,需要将东西寄存。寄存处有一个柜子,柜子有很多抽屉。
每个抽屉可放一样东西,你有两样东西要寄存,因此要了两个抽屉。

你将两样东西存放在这里。
二、数组和链表
有时候,需要在内存中存储一系列元素。假设你要编写一个管理待办事项的应用程序,为此需要将这些待办事项存储在内存中。

应该使用数组还是链表呢?鉴于数组更容易掌握,我们先将待办事项存储在数组中。使用数组意味着所有待办事项在内存中都是相连的(紧靠在一起的)。
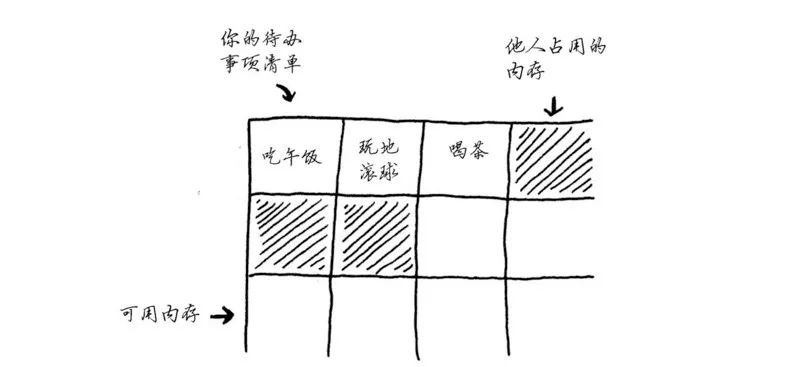
现在假设你要添加第四个待办事项,但后面的那个抽屉放着别人的东西!
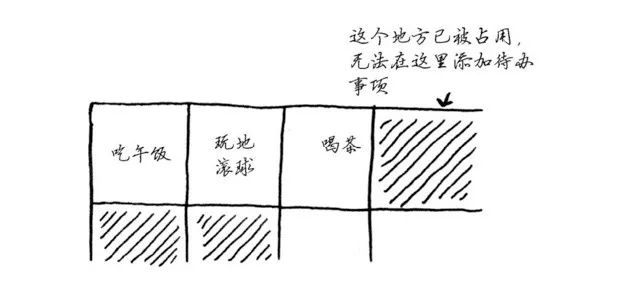
这就像你与朋友去看电影,找到地方就坐后又来了一位朋友,但原来坐的地方没有空位置,只得再找一个可坐下所有人的地方。在这种情况下,你需要请求计算机重新分配一块可容纳4个待办事项的内存,再将所有待办事项都移到那里。
如果又来了一位朋友,而当前坐的地方也没有空位,你们就得再次转移!真是太麻烦了。同样,在数组中添加新元素也可能很麻烦。如果没有了空间,就得移到内存的其他地方,因此添加新元素的速度会很慢。一种解决之道是“预留座位”:即便当前只有3个待办事项,也请计算机提供10个位置,以防需要添加待办事项。这样,只要待办事项不超过10个,就无需转移。这是一个不错的权变措施,但你应该明白,它存在如下两个缺点。
•你额外请求的位置可能根本用不上,这将浪费内存。你没有使用,别人也用不了。•待办事项超过10个后,你还得转移。因此,这种权宜措施虽然不错,但绝非完美的解决方案。对于这种问题,可使用链表来解决。
1)链表
链表中的元素可存储在内存的任何地方。
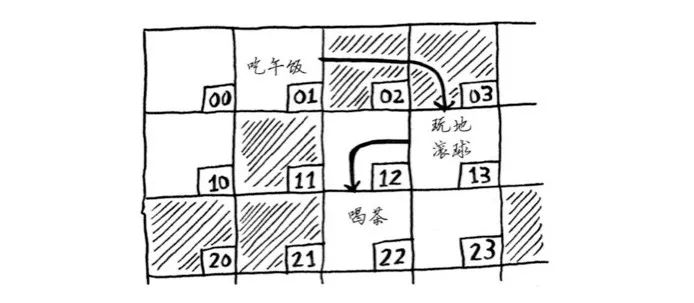
使用链表时,根本就不需要移动元素。这还可避免另一个问题。假设你与五位朋友去看一部很火的电影。你们六人想坐在一起,但看电影的人较多,没有六个在一起的座位。使用数组时有时就会遇到这样的情况。假设你要为数组分配10 000个位置,内存中有10 000个位置,但不都靠在一起。在这种情况下,你将无法为该数组分配内存!链表相当于说“我们分开来坐”,因此,只要有足够的内存空间,就能为链表分配内存。
链表的优势在插入元素方面,那数组的优势又是什么呢?
2)数组
排行榜网站使用卑鄙的手段来增加页面浏览量。它们不在一个页面中显示整个排行榜,而将排行榜的每项内容都放在一个页面中,并让你单击Next来查看下一项内容。例如,显示十大电视反派时,不在一个页面中显示整个排行榜,而是先显示第十大反派(Newman)。你必须在每个页面中单击Next,才能看到第一大反派(Gustavo Fring)。这让网站能够在10个页 面中显示广告,但用户需要单击Next 九次才能看到第一个,真的是很烦。如果整个排行榜都显示在一个页面中,将方便得多。这样,用户可单击排行榜中的人名来获得更详细的信息。

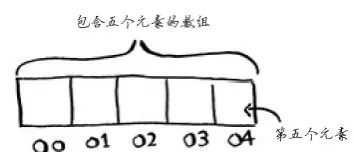
3)术语
数组的元素带编号,编号从0而不是1开始。
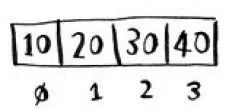
例如,在下面的数组中,元素20的位置为1.而元素10的位置为0。这通常会让新手晕头转向。从0开始让基于数组的代码编写起来更容易,因此程序员始终坚持这样做。几乎所有的编程语言都从0开始对数组元素进行编号。你很快就会习惯这种做法。元素的位置称为索引。因此,不说“元素20的位置为1”,而说“元素20位于索引1处”。
下面列出了常见的数组和链表操作的运行时间。
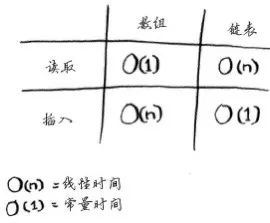
4)在中间插入
假设你要让待办事项按日期排列。之前,你在清单末尾添加了待办事项。但现在你要根据新增待办事项的日期将其插入到正确的位置。
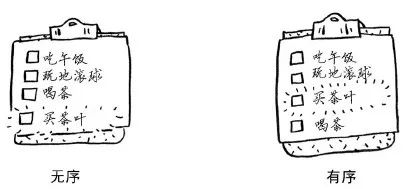
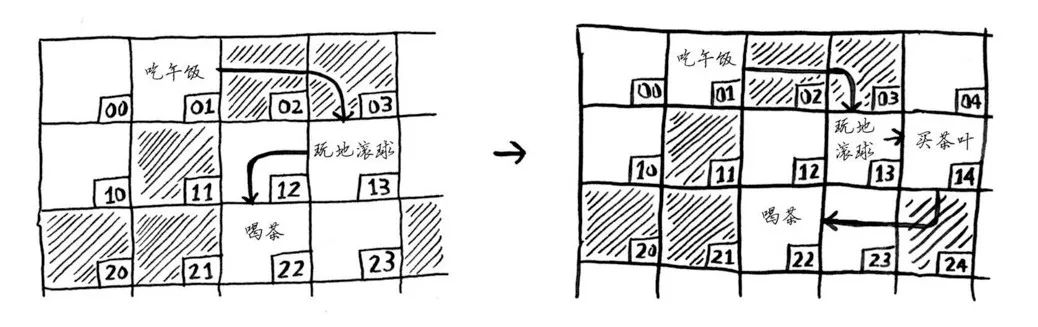
而使用数组时,则必须将后面的元素都向后移。
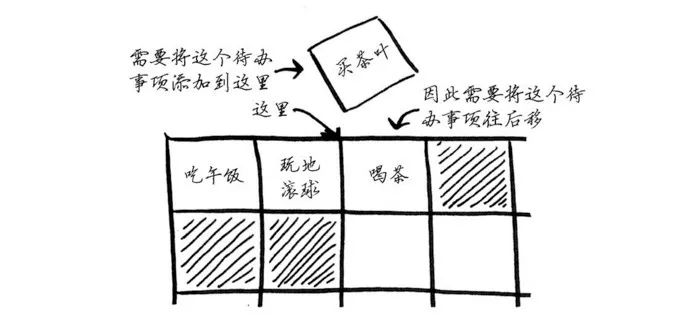
如果没有足够的空间,可能还得将整个数组复制到其他地方!因此,当需要在中间插入元素时,链表是更好的选择。
5)删除
不同于插入,删除元素总能成功。如果内存中没有足够的空间,插入操作可能失败,但在任何情况下都能够将元素删除。
下面是常见数组和链表操作的运行时间。
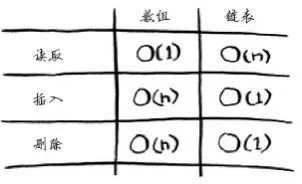
需要指出的是,仅当能够立即访问要删除的元素时,删除操作的运行时间才为O(1)。通常我们都记录了链表的第一个元素和最后一个元素,因此删除这些元素时运行时间为O(1)。
数组和链表哪个用得更多呢?显然要看情况。但数组用得很多,因为它支持随机访问。有两种访问方式:随机访问和顺序访问。顺序访问意味着从第一个元素开始逐个地读取元素。链表只能顺序访问:要读取链表的第十个元素,得先读取前九个元素,并沿链接找到第十个元素。随机访问意味着可直接跳到第十个元素。经常说数组的读取速度更快,这是因为它们支持随机访问。很多情况都要求能够随机访问,因此数组用得很多。
PS:
•不同:链表是链式的存储结构;数组是顺序的存储结构。•相同:两种结构均可实现数据的顺序存储,构造出的模型呈线性结构。
三、选择排序
有了前面的知识,你就可以学习第二种算法--选择排序。
选择排序(Selection sort) 是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
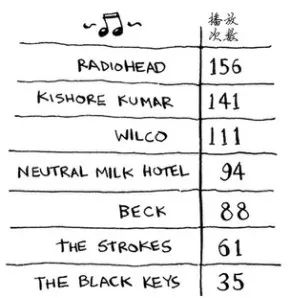
假设你的计算机存储了很多乐曲。对于每个乐队,你都记录了其作品被播放的次数。
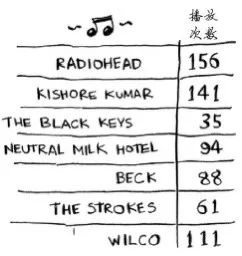
你要将这个列表按播放次数从多到少的顺序排列,从而将你喜欢的乐队排序。该如何做呢?
一种办法是遍历这个列表,找出作品播放次数最多的乐队,并将该乐队添加到一个新列表中。
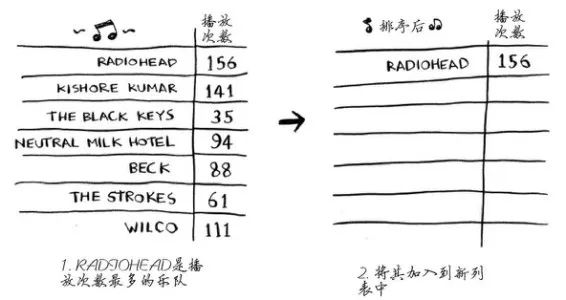
再次这样做,找出播放次数第二多的乐队。
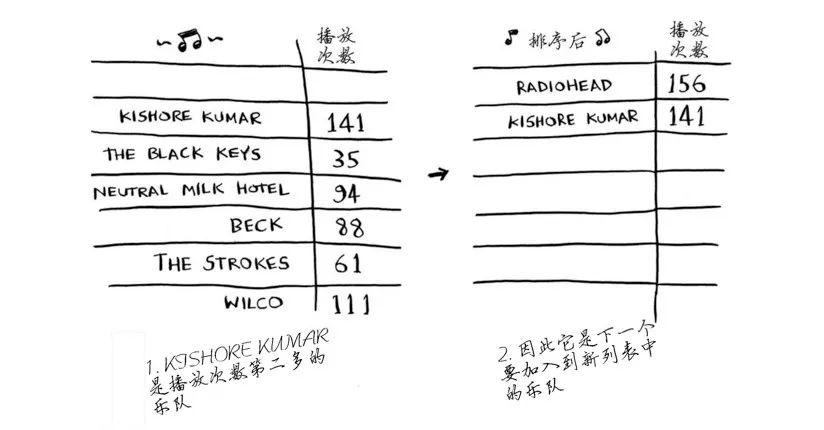
继续这样做,你将得到一个有序列表。
下面从计算机科学的角度出发,看看这需要多长时间。别忘了,O(n)时间意味着查看列表中的每个元素一次。例如,对乐队列表进行简单查找时,意味着每个乐队都要查看一次。
要找出播放次数最多的乐队,必须检查列表中的每个元素。正如你刚才看到的,这需要的时间为O(n)。因此对于这种时间为O(n)的操作,你需要执行n次。
需要的总时间为 O(n×n),即O(n^2)。排序算法很有用。你现在可以对如下内容进行排序:
选择排序是一种灵巧的算法,但其速度不是很快。快速排序是一种更快的排序算法,其运行时间为O(n log n),这将在下一章介绍。
前面没有列出对乐队进行排序的代码,但下述代码提供了类似的功能:将数组元素按从小到大的顺序排列。先编写一个用于找出数组中最小元素的函数。
python版本代码如下:
def findSmallest(arr):# 存储最小的值smallest = arr[0]# 存储最小元素的索引smallest_index = 0for i in range(1, len(arr)):if arr[i] < smallest:smallest_index = ismallest = arr[i]return smallest_index# 对数组进行排序def selectionSort(arr):newArr = []for i in range(len(arr)):# 查找数组中最小的元素并将其添加到新数组中smallest = findSmallest(arr)newArr.append(arr.pop(smallest))return newArrprint(selectionSort([5, 3, 6, 2, 10]))
[2, 3, 5, 6, 10]
java版本代码如下:
public static void selectionSort(int[] arr) {for (int i = 0; i < arr.length - 1; i++) {int min = i;for (int j = i + 1; j < arr.length; j++) {if (arr[min] > arr[j]) {min = j;}}if (min != i) {int tmp = arr[min];arr[min] = arr[i];arr[i] = tmp;}}}
四、总结
参考
•百度百科•《算法图解》
以上是关于笔记 选择排序的主要内容,如果未能解决你的问题,请参考以下文章