数据结构学习笔记——选择排序(简单选择排序和堆排序)
Posted 晚风(●•σ )
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习笔记——选择排序(简单选择排序和堆排序)相关的知识,希望对你有一定的参考价值。
目录
一、简单选择排序
(一)排序思想
以递增为例,在每一趟的简单选择排序过程中,每次选取当前元素最小的元素,将其作为有序子序列的第i,i+1,……个元素,依次进行下去,即和第一个元素交换,依次进行交换,直到剩余一个元素,此时整个序列已经有序,每一趟简单选择排序可确定一个元素的最终位置。
递增的简单选择排序代码如下:
/*简单选择排序(递增)*/
void SelectSort1(int r[],int n)
int i,j,min,temp;
for(i=0; i<n-1; i++) //for循环进行n-1趟
min=i; //min变量记录最小元素的位置
for(j=i+1; j<n; j++) //从无序序列中选择一个最小的元素
if(r[j]<r[min])
min=j;
temp=r[i]; //将最小元素与无序序列的第一个关键字进行交换
r[i]=r[min];
r[min]=temp;
同样,递减的简单选择排序代码如下:
/*简单选择排序(递减)*/
void SelectSort2(int r[],int n)
int i,j,max,temp;
for(i=0; i<n-1; i++) //for循环进行n-1趟
max=i; //max变量记录最小元素的位置
for(j=i+1; j<n; j++) //从无序序列中选择一个最大的元素
if(r[j]>r[max])
max=j;
temp=r[i]; //将最大元素与无序序列的第一个关键字进行交换
r[i]=r[max];
r[max]=temp;
例如,对于一个序列-2,0,7,1,4,3进行简单选择排序,输出其递增和递减序列,代码如下:
#include<stdio.h>
#define MAXSIZE 100
/*创建函数*/
void Create(int r[],int n)
for(int i=0; i<n; i++)
printf("输入第%d个元素:",i+1);
scanf("%d",&r[i]);
/*输出函数*/
void Display(int r[],int n)
for(int i=0; i<n; i++)
printf("%d ",r[i]);
/*简单选择排序(递增)*/
void SelectSort1(int r[],int n)
int i,j,min,temp;
for(i=0; i<n-1; i++) //for循环进行n-1趟
min=i; //min变量记录最小元素的位置
for(j=i+1; j<n; j++) //从无序序列中选择一个最小的元素
if(r[j]<r[min])
min=j;
temp=r[i]; //将最小元素与无序序列的第一个关键字进行交换
r[i]=r[min];
r[min]=temp;
/*简单选择排序(递减)*/
void SelectSort2(int r[],int n)
int i,j,max,temp;
for(i=0; i<n-1; i++) //for循环进行n-1趟
max=i; //max变量记录最小元素的位置
for(j=i+1; j<n; j++) //从无序序列中选择一个最大的元素
if(r[j]>r[max])
max=j;
temp=r[i]; //将最大元素与无序序列的第一个关键字进行交换
r[i]=r[max];
r[max]=temp;
/*主函数*/
int main()
int n;
int r[MAXSIZE];
printf("请输入排序表的长度:");
scanf("%d",&n);
Create(r,n);
printf("已建立的序列为:\\n");
Display(r,n);
SelectSort1(r,n);
printf("\\n");
printf("递增排序后的序列为:\\n");
Display(r,n);
SelectSort2(r,n);
printf("\\n");
printf("递减排序后的序列为:\\n");
Display(r,n);
运行结果如下:
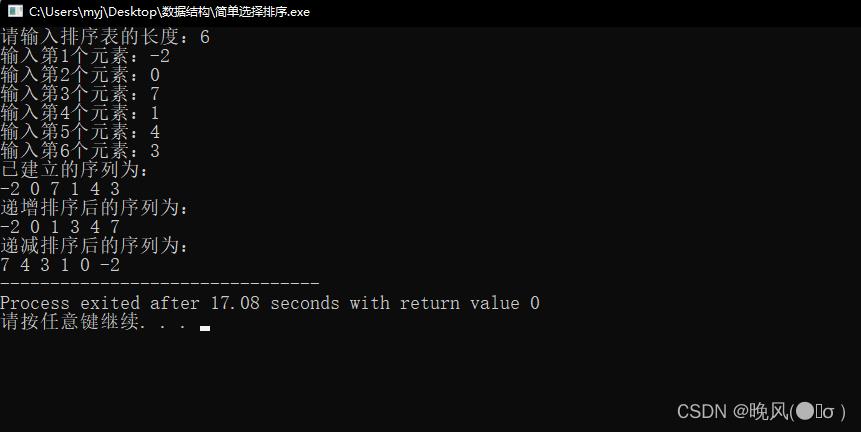
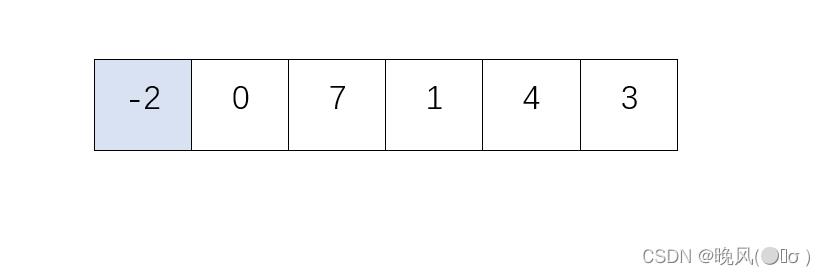
简单选择排序
1、第一趟简单选择排序,从左往右搜索最小的元素,找到-2,将该元素与第一个元素进行交换,由于-2本身处于第一个元素位置,未发生交换;
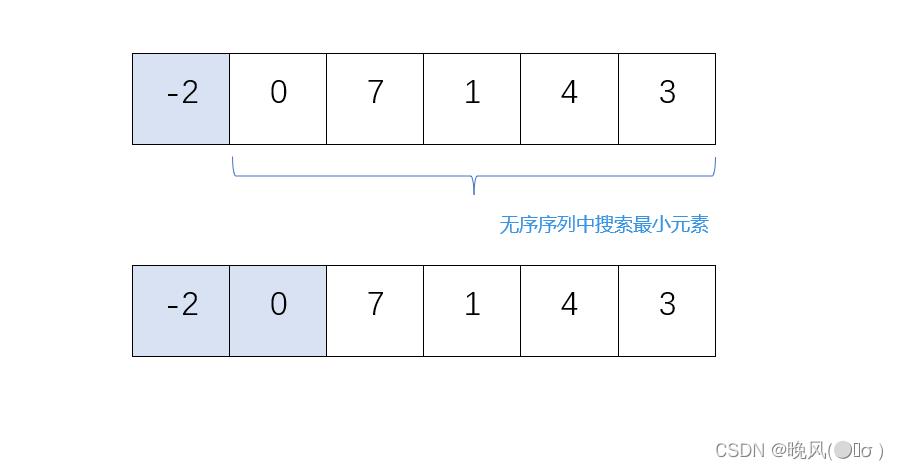
2、第二趟简单选择排序,在剩下的无序序列中,从左往右搜索最小的元素,找到0,将该元素与第二个元素进行交换,由于0本身处于第二个元素位置,未发生交换;
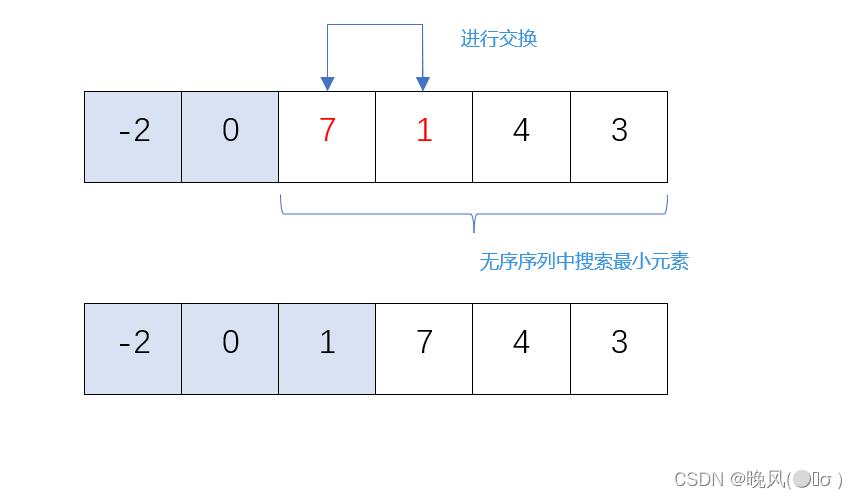
3、第三趟简单选择排序,在剩下的无序序列中,从左往右搜索最小的元素,找到1,将该元素与第三个元素7进行交换;
4、第四趟简单选择排序,在剩下的无序序列中,从左往右搜索最小的元素,找到3,将该元素与第四个元素7进行交换;
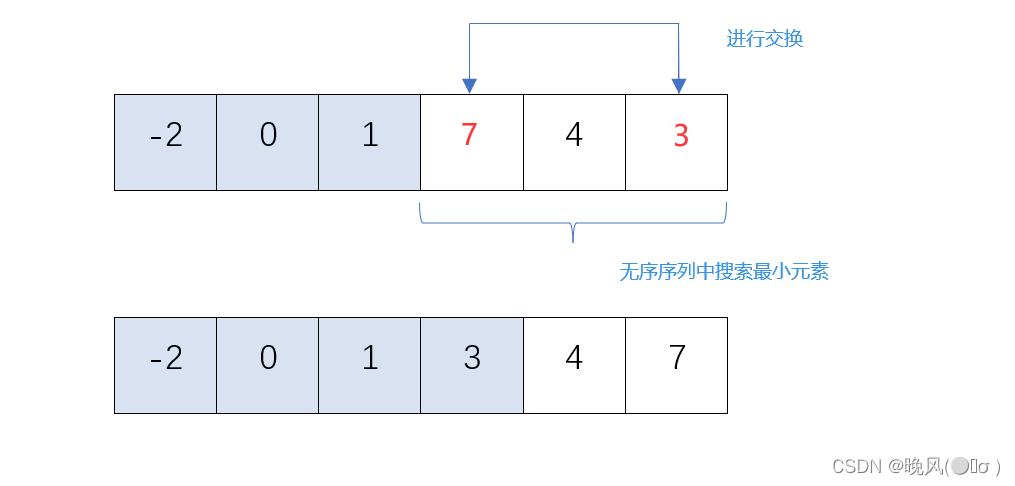
5、第五趟简单选择排序,在剩下的无序序列中,从左往右搜索最小的元素,找到4,未发生交换;
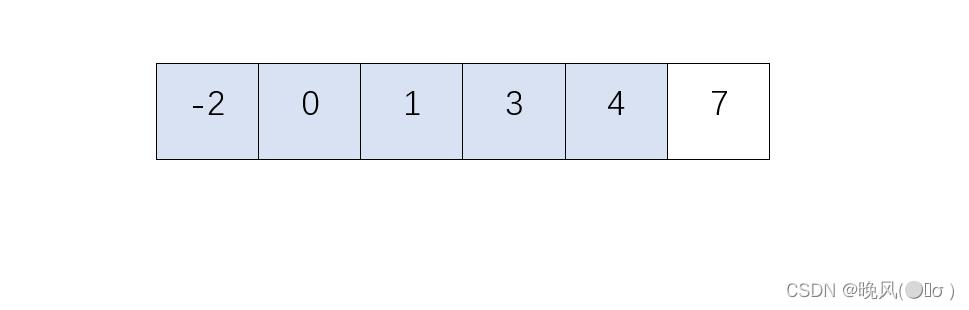
此时整个序列已经有序,可以得出,共进行n-1趟排序过程。
(二)算法分析
分析:
(1)空间复杂度:由于额外辅助空间只有一个temp变量,为参数级,所以简单选择排序的空间复杂度为O(1);
(2)时间复杂度:元素之间的比较次数与初始序列无关,即每次的比较分别是n-1,n-2,……,2,1,即n(n-1)/2=n2/2,所以时间复杂度为O(n2)。
(4)稳定性:简单选择排序是一种不稳定的排序算法。
(5)适用性:简单选择排序可适用于顺序存储和链式存储的线性表。
(6)排序方式:简单选择排序是一种内部排序(In-place)。
二、堆排序
(一)排序思想
1、堆树和大、小根堆
堆排序是利用堆树来进行排序,可以将其视为一棵完全二叉树,树中每一个结点均大于或等于其两个子结点的值,根结点是堆树中的最小值或最大值,即对应小根堆和大根堆。
| 名称 | 备注 |
|---|---|
| 小根堆 | 根结点≥左孩子,右孩子 |
| 大根堆 | 根结点≤左孩子,右孩子 |
基于小根堆得到的序列为递减序列,基于大根堆得到的序列为递增序列。
2、调整根堆
顺序存储的完全二叉树(若结点为i):
①i的左孩子结点,则为2i;
②i的右孩子结点,则为2i+1;
③i的父结点,则为⌊ i/2 ⌋。
以下以调整大根堆为例,
对于一个大根堆,检查所有非终端结点是否满足大根堆的要求(根结点≤左孩子,右孩子),不满足则进行调整:若当前结点的元素小于左、右孩子中较大者元素,则将当前结点与较大者元素进行交换,使该子树成为堆,若因元素交换破坏了下一级的堆顺序,使不满足堆的性质,则向下继续进行调整。
调整堆的代码如下:
/*堆调整*/
void Adjust(int r[],int low,int high)
int i=low,j=2*i; //r[j]是r[i]的左孩子结点
int temp=r[i];
while(j<=high)
if(j<high&&r[j]<r[j+1]) //若当前结点的右孩子较大,则将j指向右孩子
j++;
if(temp<r[j])
r[i]=r[j]; //将r[j]调整至双亲结点的位置上,互换
i=j; //修改i和j的值,以便继续调整
j=2*i;
else
break; //调整结束
r[i]=temp; //将被调整的结点放到其应当的位置
1、初始堆树如下:
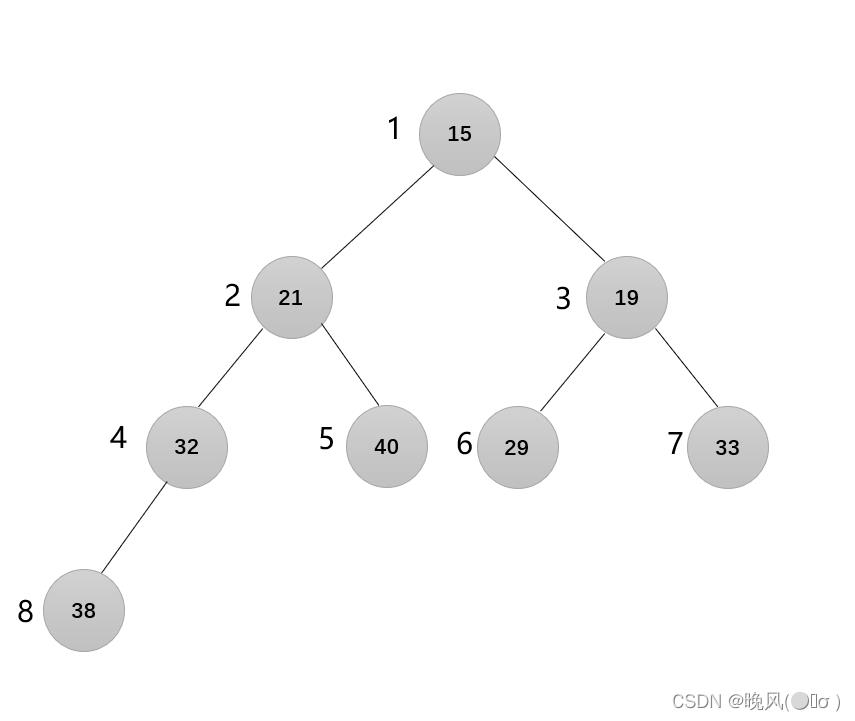
2、根据完全二叉树的性质,由下至上进行调整
在顺序存储的完全二叉树中,非叶子结点的编号i≤⌊N/2 ⌋。
由于N=8,可得非叶子结点的编号i≤⌊N/2 ⌋=⌊8/2 ⌋=4,检查所有非终端结点是否满足大根堆的要求,即检查i≤4的结点,且按照从下往上的顺序依次检查。
3、i=4,结点32不满足要求:
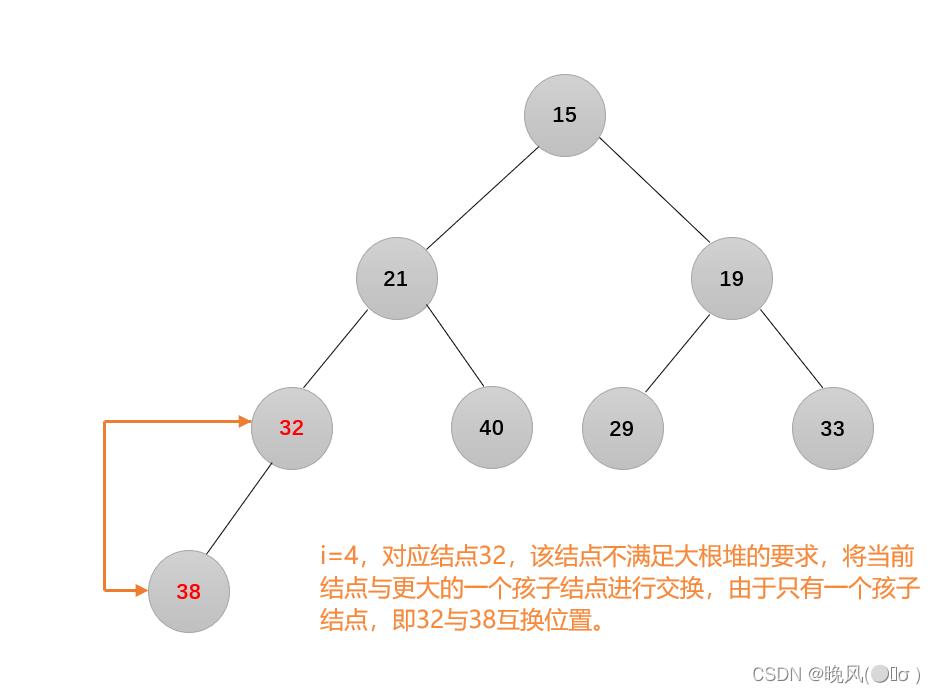
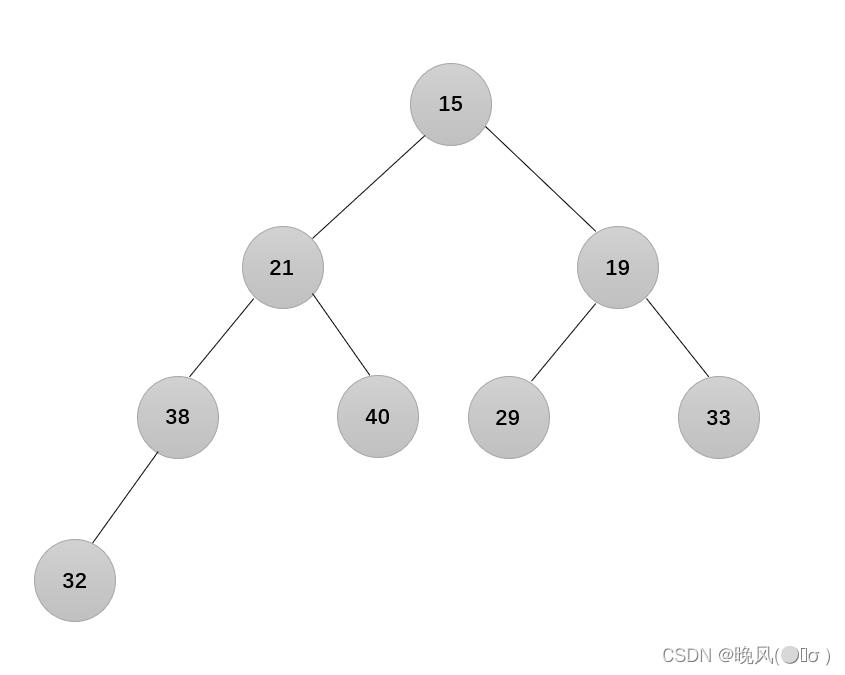
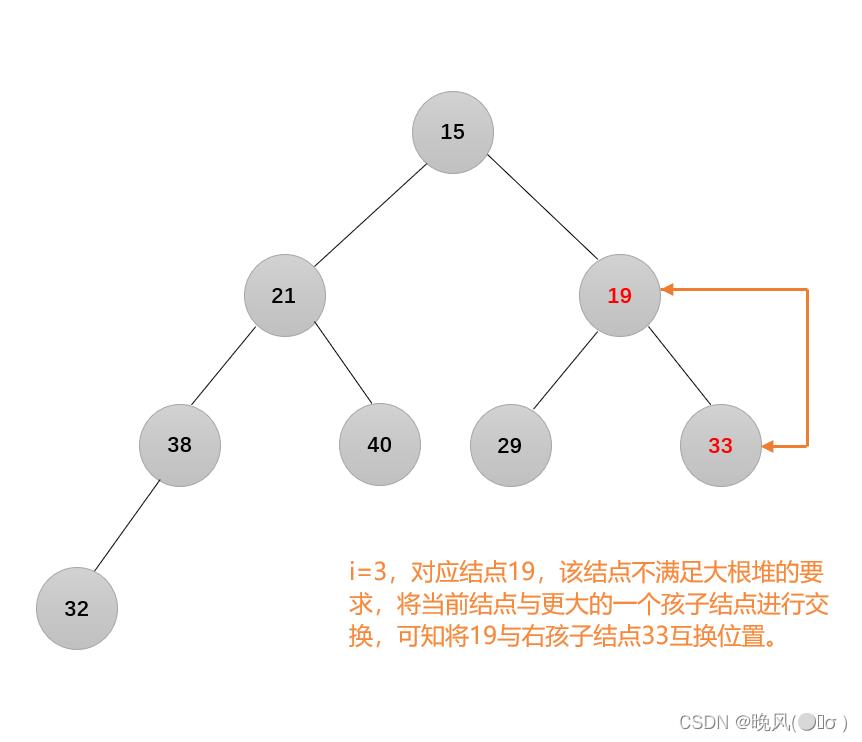
4、i=3,结点19不满足要求:
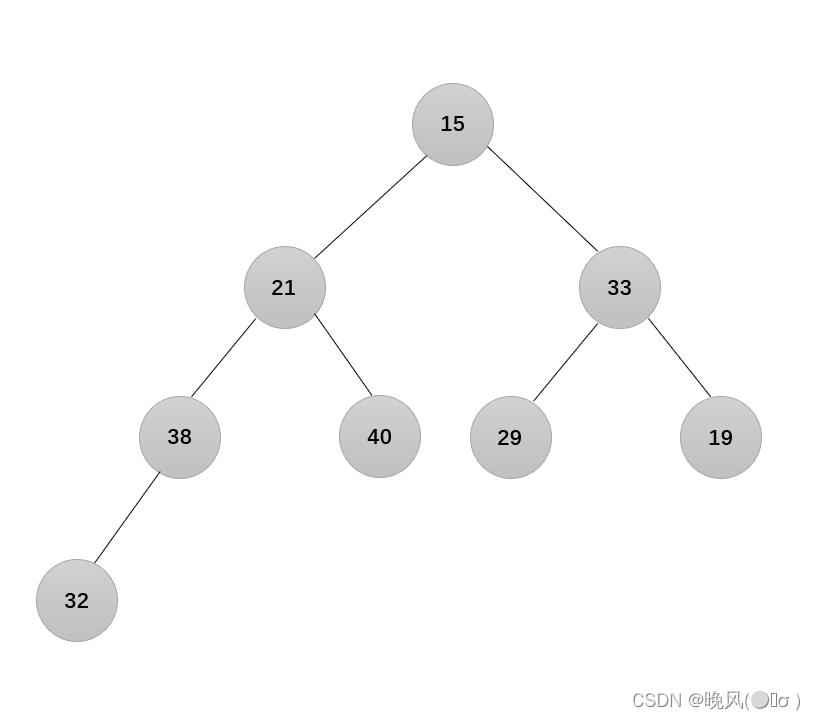
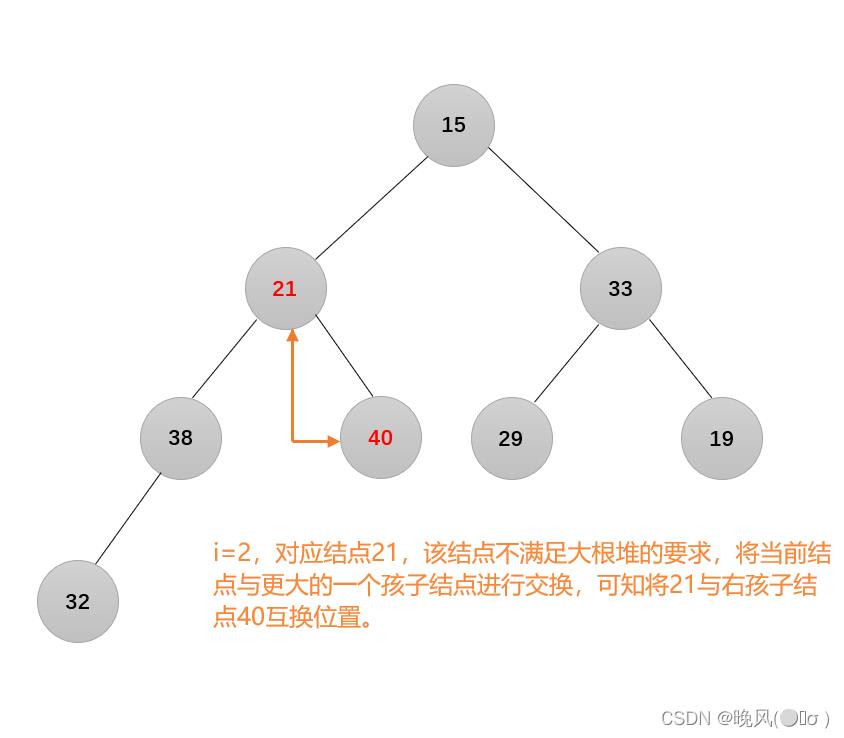
5、i=2,结点21不满足要求:
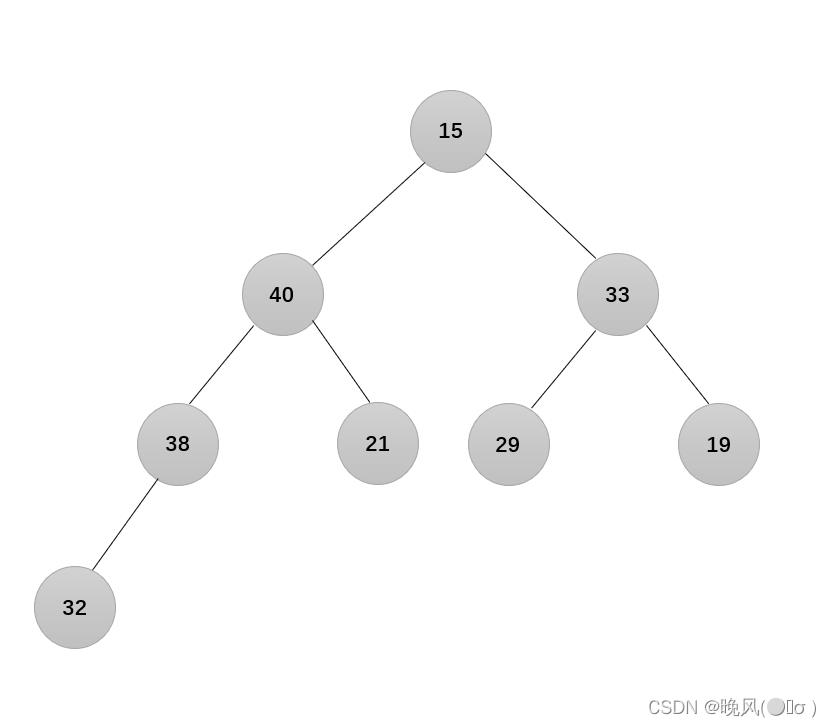
6、i=1,结点15不满足要求:
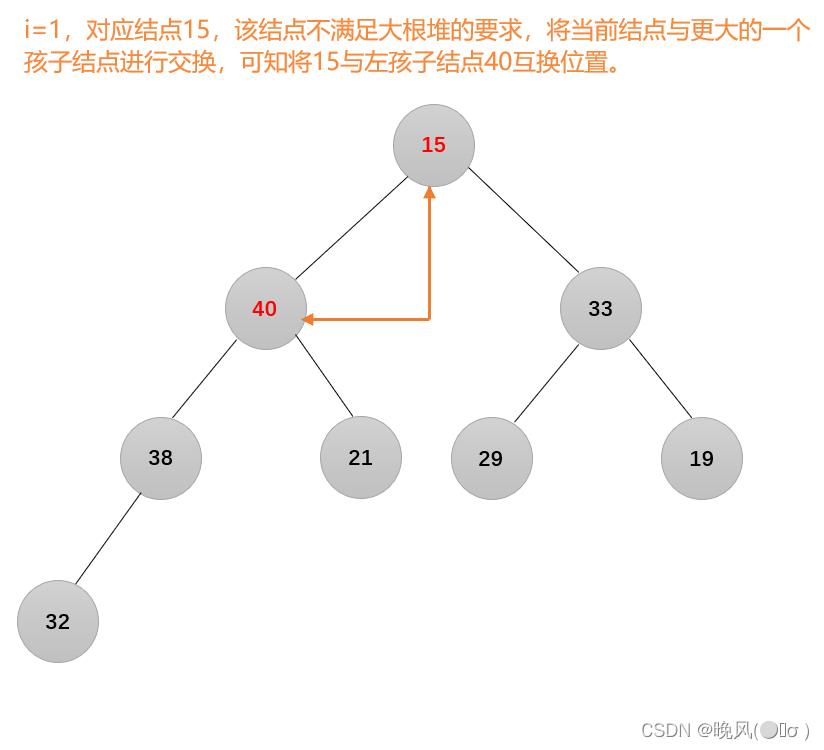
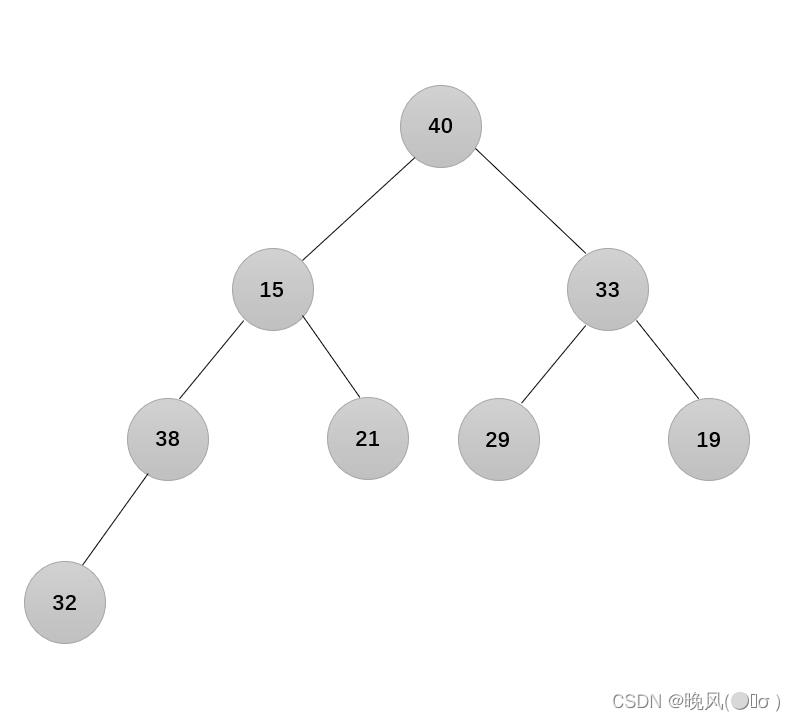
7、由于经过以上的几轮交换后,可发现结点15不满足大根堆的要求,向下继续进行调整:
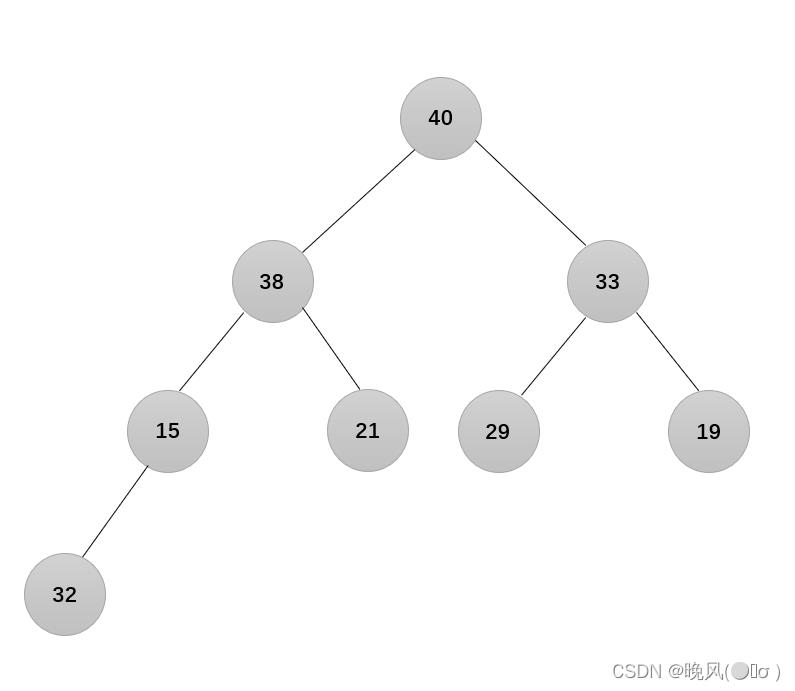
还需调整:
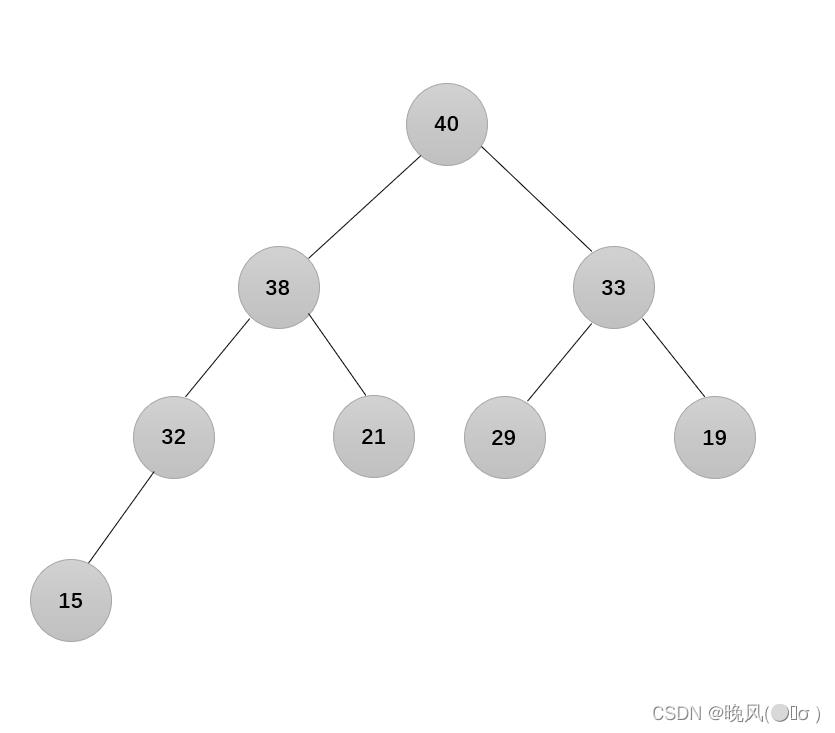
至此,该完全二叉树符合堆的定义。
3、堆排序
在建立根堆后,将堆中堆顶元素与堆的最后一个元素进行交换,堆顶元素进入有序序列到达最终位置(从无序序列中被排出,符合选择排序的过程),然后对剩下的无序序列继续进行调整,依次进行下去,……,直到无序序列中剩余最后一个元素,此时整个序列已经有序,堆排序结束。
堆排序的代码如下:
/*堆排序*/
void HeapSort(int r[],int n)
int i,temp;
for(i=n/2;i>=1;i--) //建立初始堆
Adjust(r,i,n);
for(i=n;i>1;i--) //进行n-1次循环,完成堆排序
temp=r[1]; //将堆中最后一个元素与堆顶元素交换,将其放入最终位置
r[1]=r[i];
r[i]=temp;
Adjust(r,1,i-1); //对剩下的无序序列进行调整
1、第一趟,将堆顶元素与堆的最后一个元素进行交换,将堆顶元素加入有序子序列,即40与15交换:
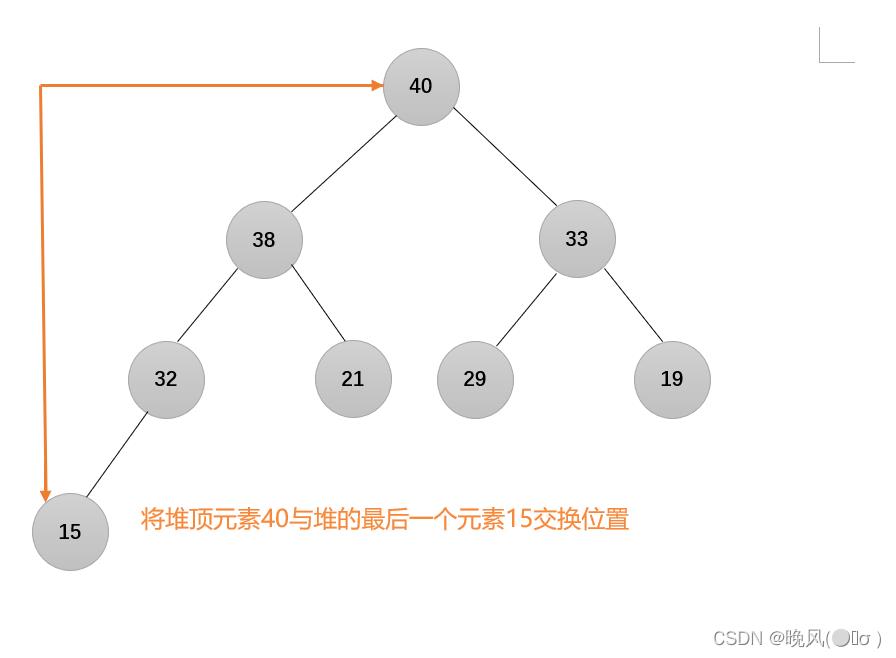
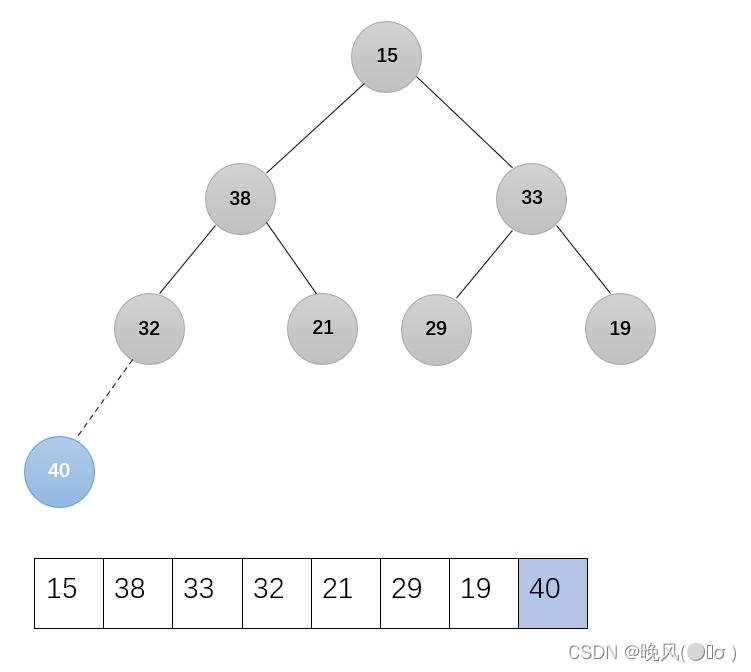
可看出,此时序列中不满足大根堆的要求(不包括有序子序列40),所以需要恢复大根堆,剩下的无序序列调整为大根堆,调用函数Adjust(r,1,7):
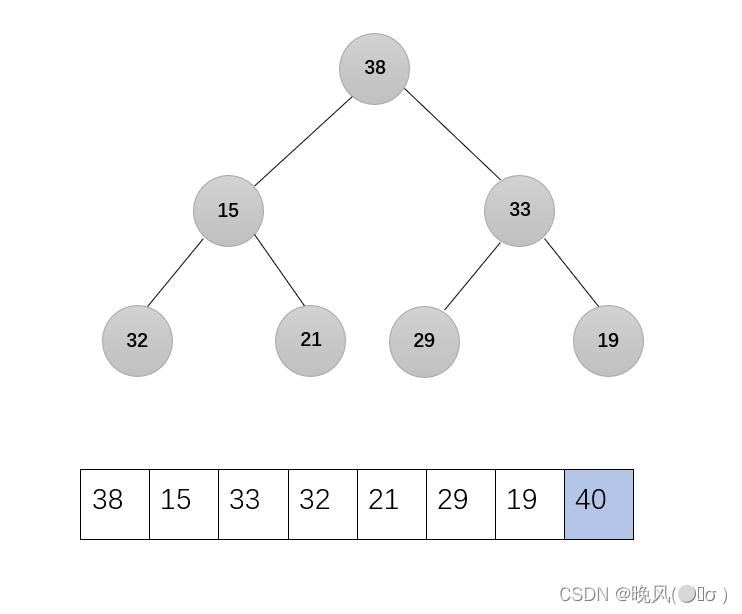
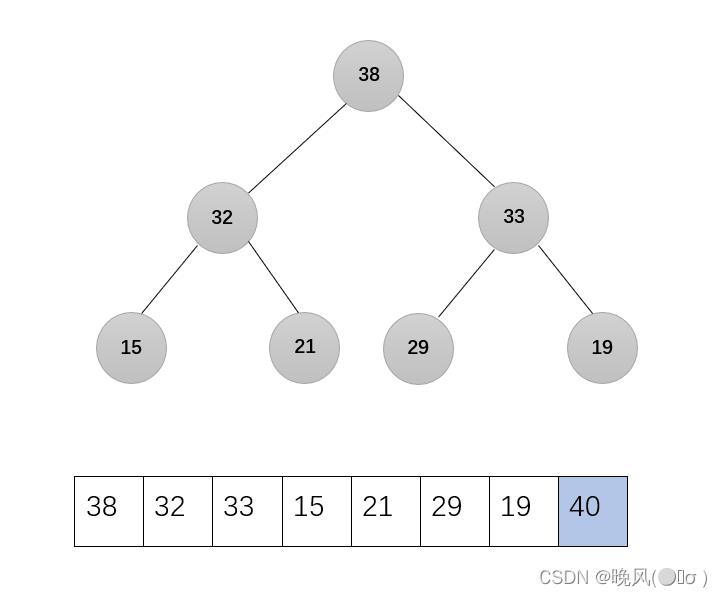
2、第二趟操作也是一样,将堆顶元素与堆的最后一个元素进行交换,将堆顶元素加入有序子序列,即38与19交换:
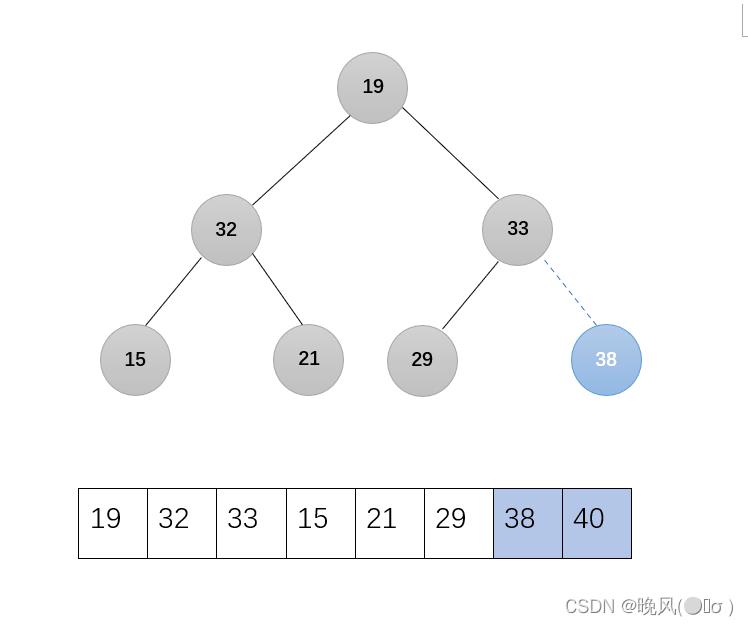
剩下的无序序列调整为大根堆,调用函数Adjust(r,1,6):
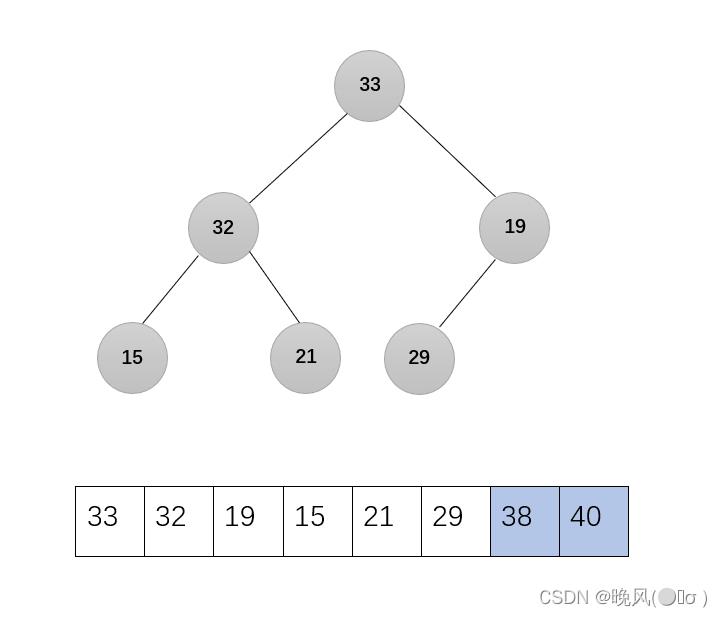
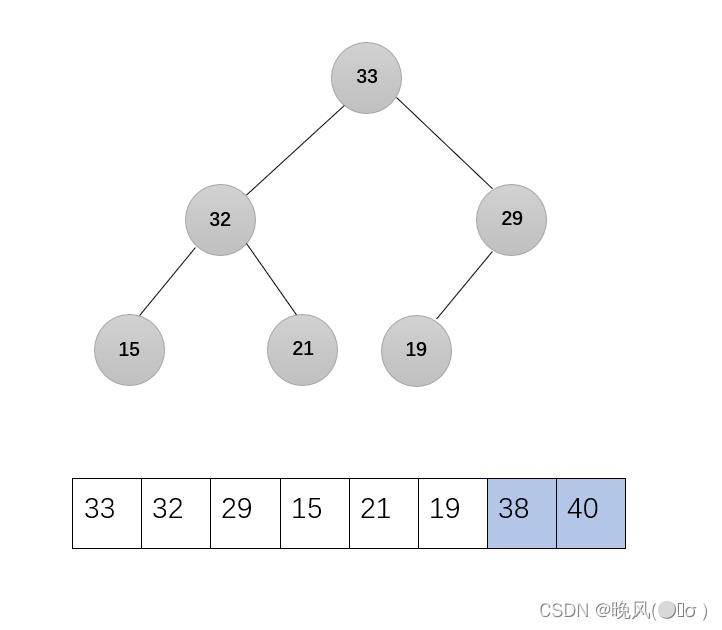
3、第三趟,33与19交换:
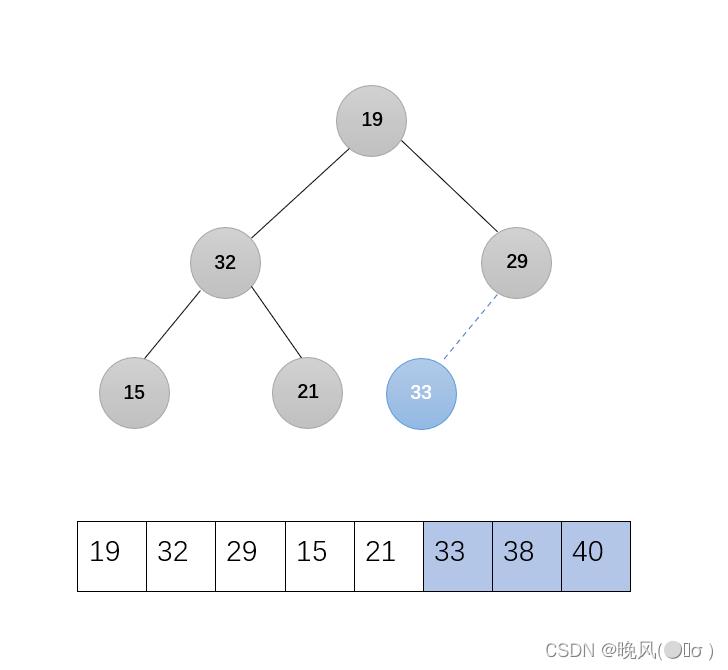
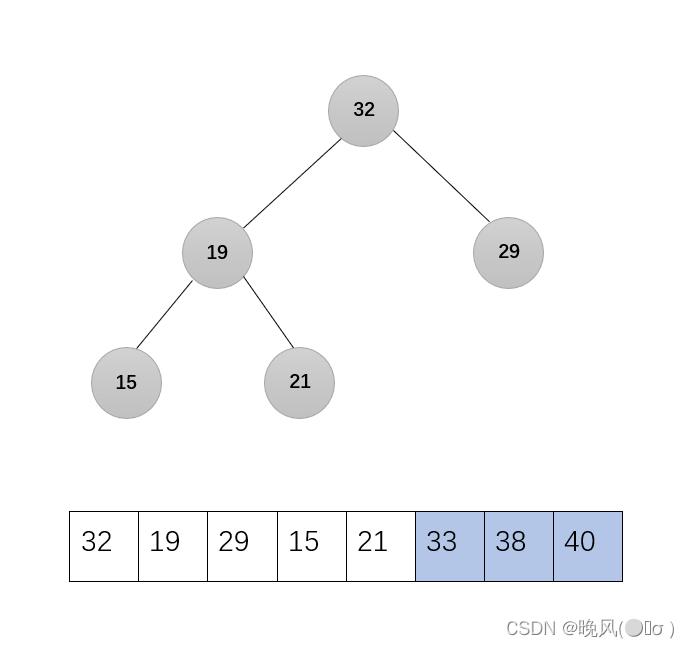
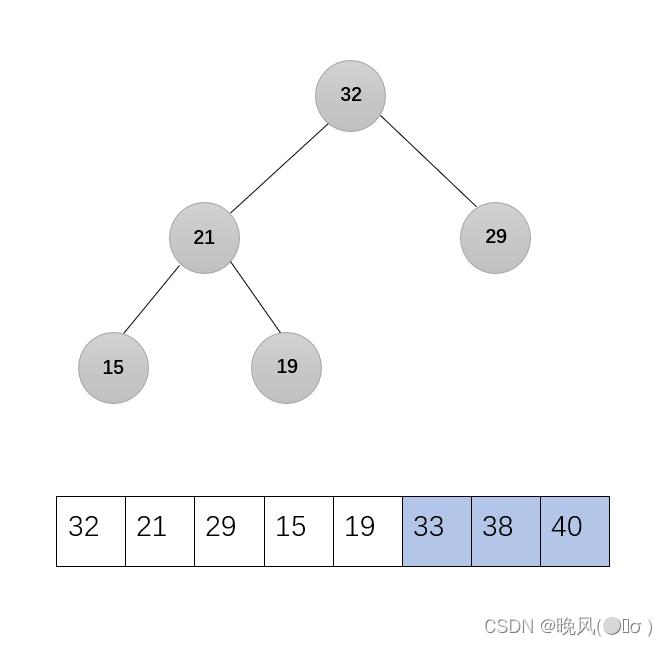
剩下的无序序列调整为大根堆,调用函数Adjust(r,1,5):
4、第四趟,32与19交换:
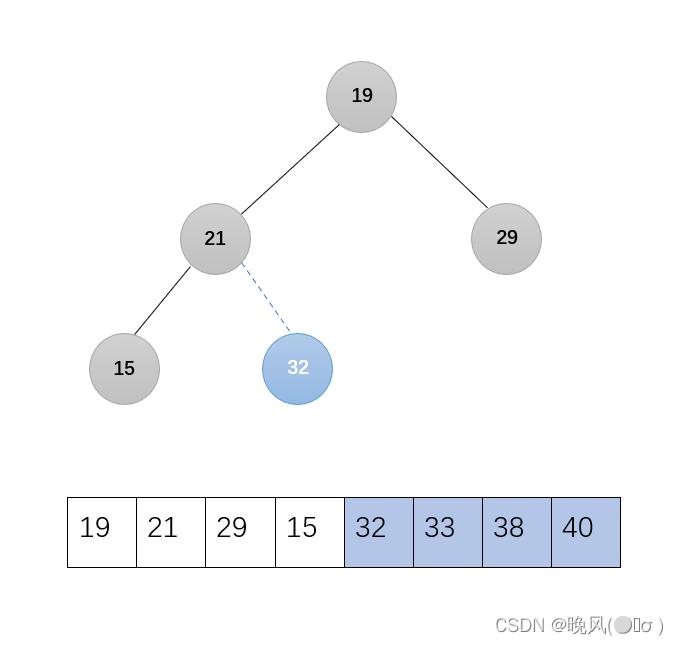
剩下的无序序列调整为大根堆,调用函数Adjust(r,1,4):
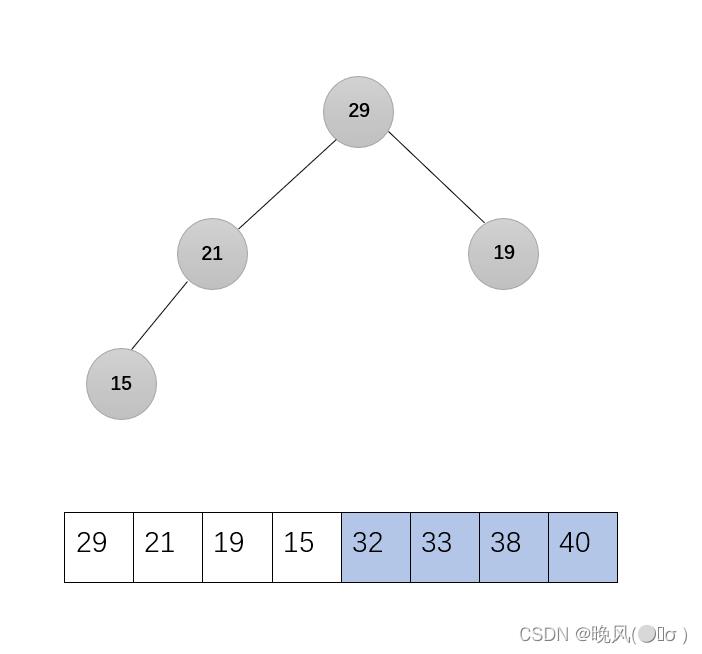
5、第五趟,29与15交换:
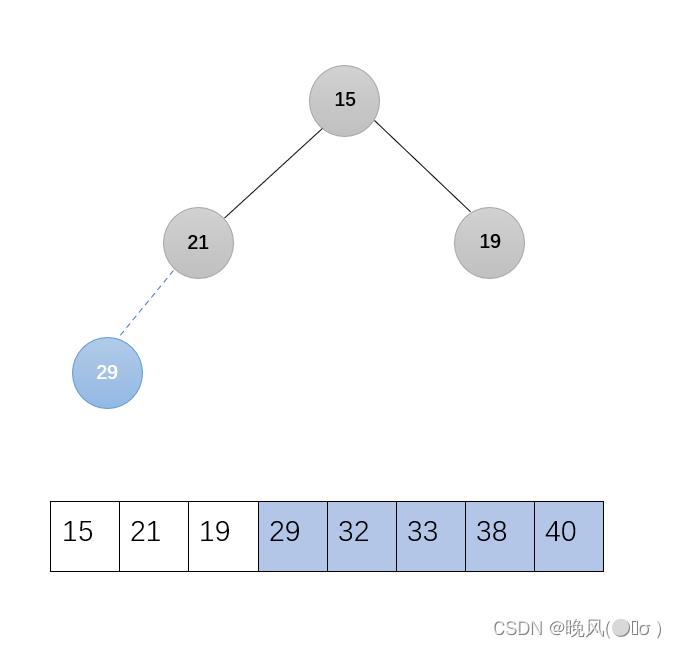
剩下的无序序列调整为大根堆,调用函数Adjust(r,1,3):
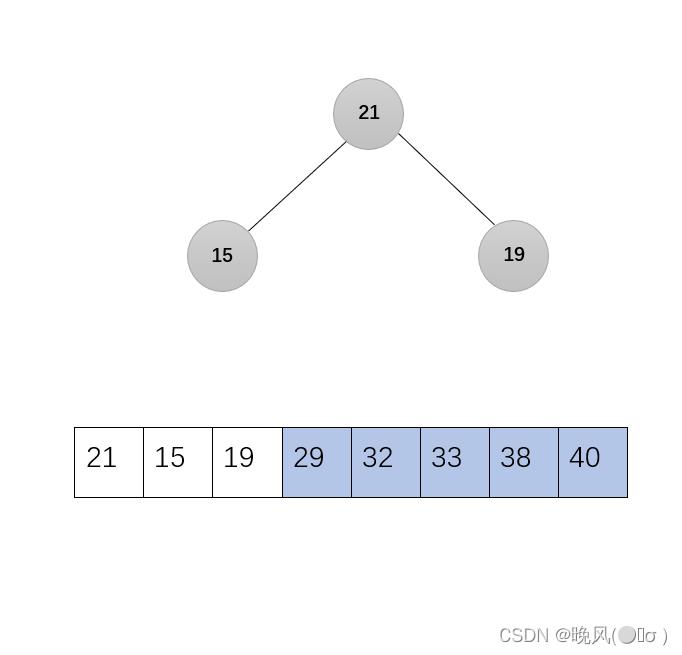
6、第六趟,21与19交换:
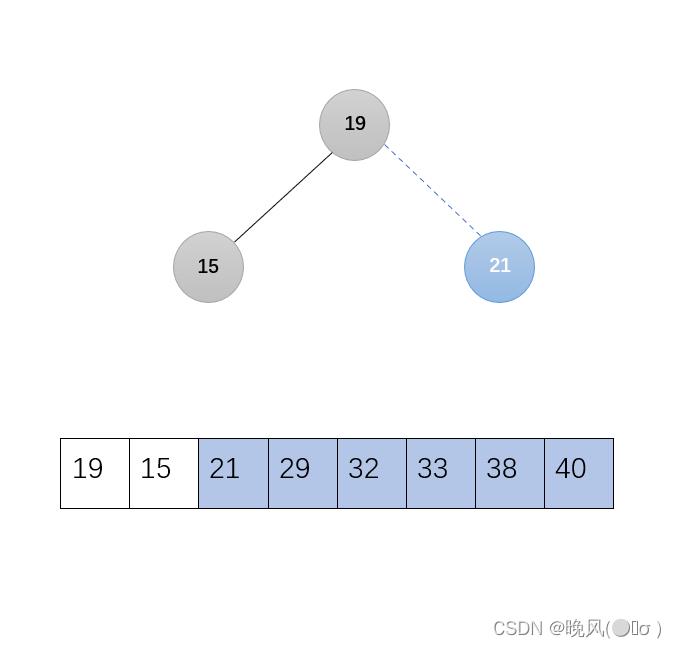
剩下的无序序列调整为大根堆,调用函数Adjust(r,1,2):
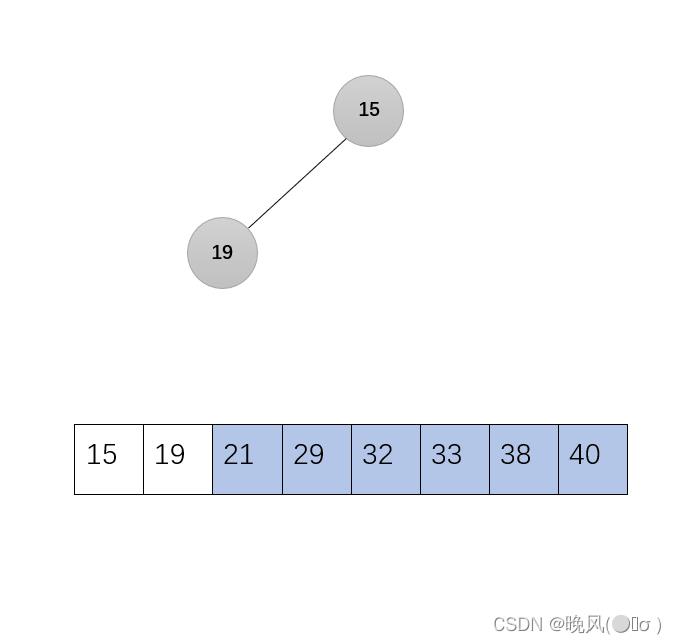
7、第七趟,由于符合大根堆,不用交换:
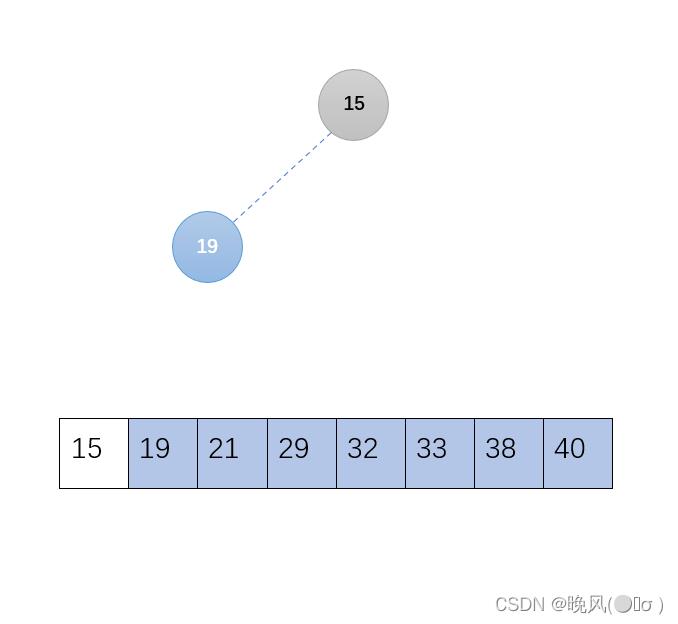
剩下最后一个元素,结束,此时得到的序列即为最终结果:
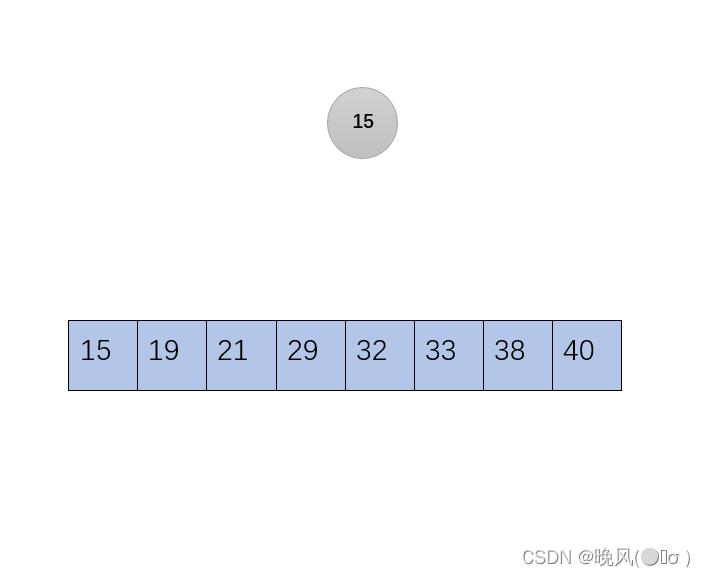
整体代码如下:
#include<stdio.h>
#define MAXSIZE 100
/*创建函数*/
void Create(int r[],int n)
for(int i=0; i<n; i++)
printf("输入第%d个元素:",i+1);
scanf("%d",&r[i]);
/*输出函数*/
void Display(int r[],int n)
for(int i=0; i<n; i++)
printf("%d ",r[i]);
/*堆调整*/
void Adjust(int r[],int low,int high)
int i=low,j=2*i; //r[j]是r[i]的左孩子结点
int temp=r[i];
while(j<=high)
if(j<high&&r[j]<r[j+1]) //若当前结点的右孩子较大,则将j指向右孩子
j++;
if(temp<r[j])
r[i]=r[j]; //将r[j]调整至双亲结点的位置上,互换
i=j; //修改i和j的值,以便继续调整
j=2*i;
else
break; //调整结束
r[i]=temp; //将被调整的结点放到其应当的位置
/*堆排序*/
void HeapSort(int r[],int n)
int i,temp;
for(i=n/2;i>=1;i--) //建立初始堆
Adjust(r,i,n);
for(i=n;i>1;i--) //进行n-1次循环,完成堆排序
temp=r[1]; //将堆中最后一个元素与堆顶元素交换,将其放入最终位置
r[1]=r[i];
r[i]=temp;
Adjust(r,1,i-1); //对剩下的无序序列进行调整
/*主函数*/
int main()
int n;
int r[MAXSIZE];
printf("请输入排序表的长度:");
scanf("%d",&n);
Create(r,n);
printf("已建立的序列为:\\n");
Display(r,n);
HeapSort(r,n);
printf("\\n");
printf("排序后的序列为:\\n");
Display(r,n);
运行结果如下:
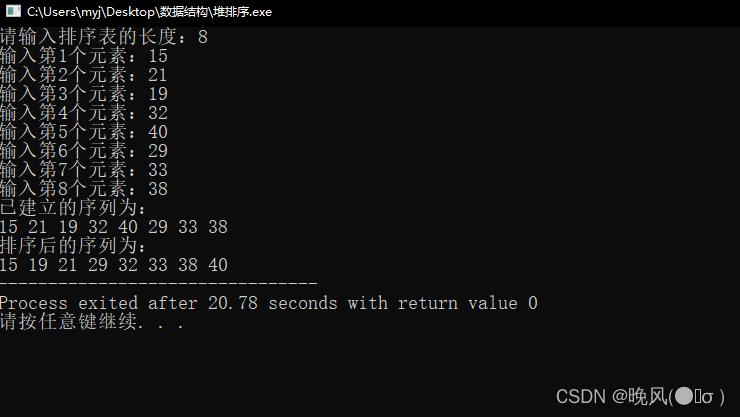
(二)算法分析
分析:
(1)构建n个记录的初始堆所需的时间复杂度为O(n);
(2)空间复杂度:堆排序的空间复杂度为O(1);
(3)时间复杂度:初始建堆的时间复杂度为O(n),建堆过程中元素对比次数不超过4n,n-1趟交换和建堆过程中,根结点最多下坠h-1层,每下坠一层最多只需对比元素两次,每一趟不超过O(h)=O(log2n),即堆排序的时间复杂度为O(nlog2n),故堆排序的时间复杂度均为O(n)+O(nlog2n)=O(nlog2n)。
(4)稳定性:堆排序是一个不稳定的排序算法。
(5)适用性:堆排序只能用于顺序存储结构。
(6)排序方式:堆排序是一种内部排序(In-place)。
三、堆的插入、删除
(一)堆的插入
对堆进行插入操作时,将要插入的结点放在堆的末尾,插入后,整个完全二叉树仍需满足堆的要求,对该结点进行向上调整,每次上升操作需对比元素1次,由于完全二叉树的高度为h=⌊log2n⌋+1,所以向n个结点的堆中插入一个新元素的时间复杂度为O(log2n)。
已知序列25,13,10,12,9是大根堆,在序列尾部插入新元素18,将其再调整为大根堆,调整过程中元素之间进行的比较次数为__________。
初始大根堆序列:
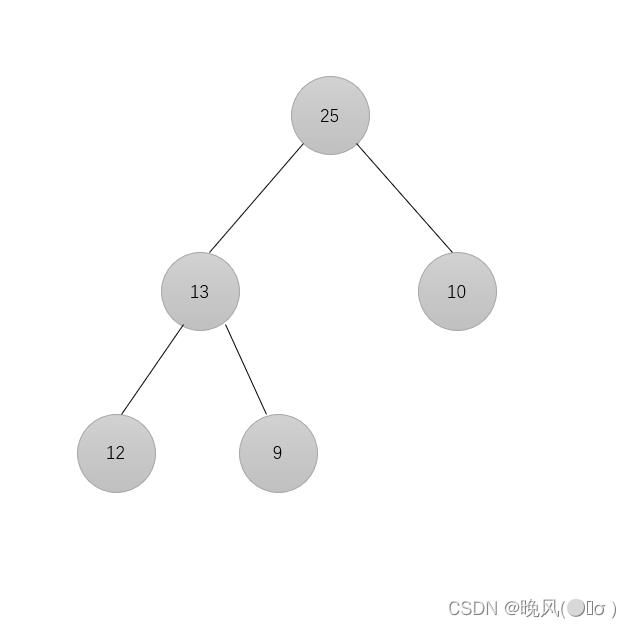
插入结点,在序列尾部插入元素18:
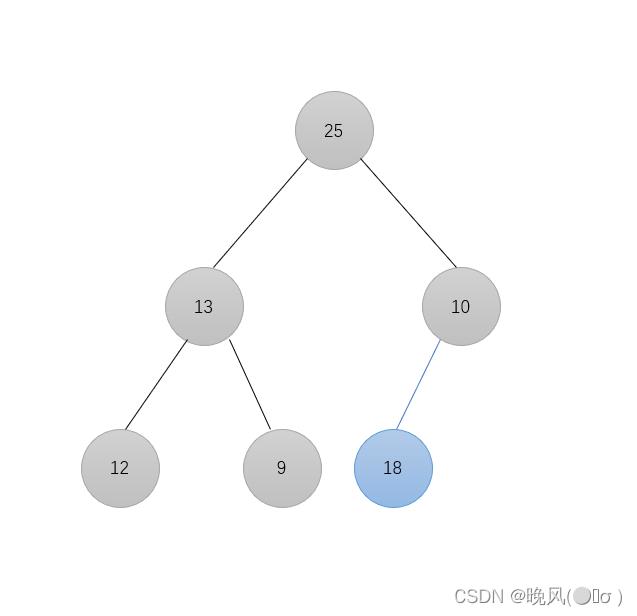
不符合大根堆要求,进行调整,18与10进行比较,然后交换位置:
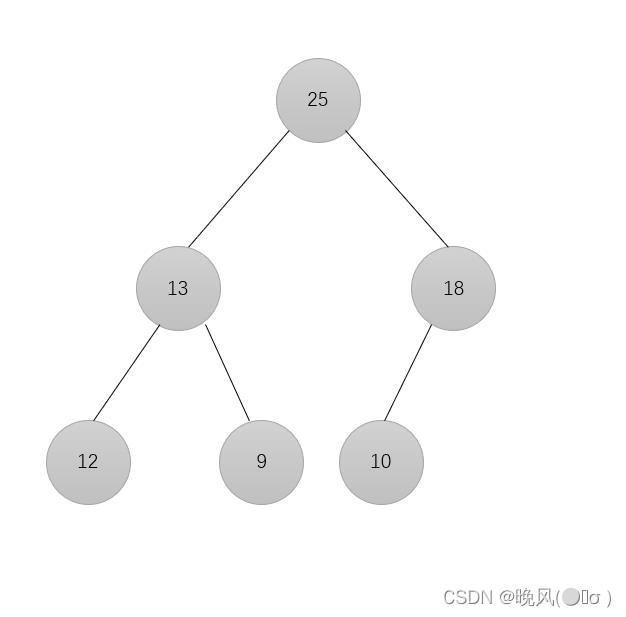
18与25比较,符合大根堆要求,不用交换,故一共比较次数为2。
(二)堆的删除
对堆进行删除操作时,删除的结点的位置就会空出来,此时需要将堆的末尾元素填到该位置,然后下调至合适位置,每次下调需对比元素1次或2次,删除操作也是取决于树的高度,即时间复杂度为O(log2n)。
已知小根堆为8,15,10,21,34,16,12,删除关键字8之后需重新建堆,在此过程中,关键字之间的比较次数是_________。
初始小根堆序列:
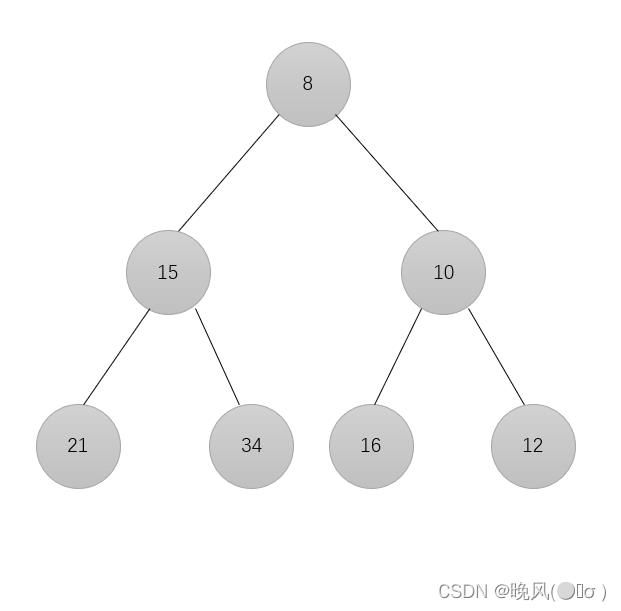
删除结点,删除元素8,将末尾元素12填上:
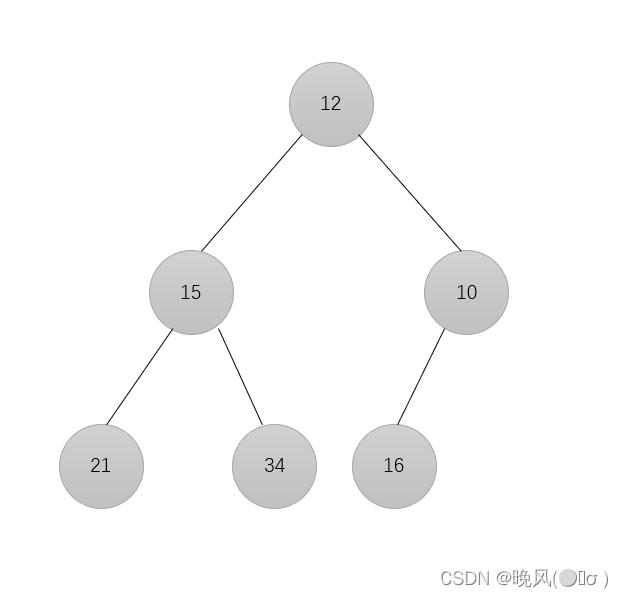
进行调整,12与15比较,不用交换;由于10小于12,所以交换10和12的位置:
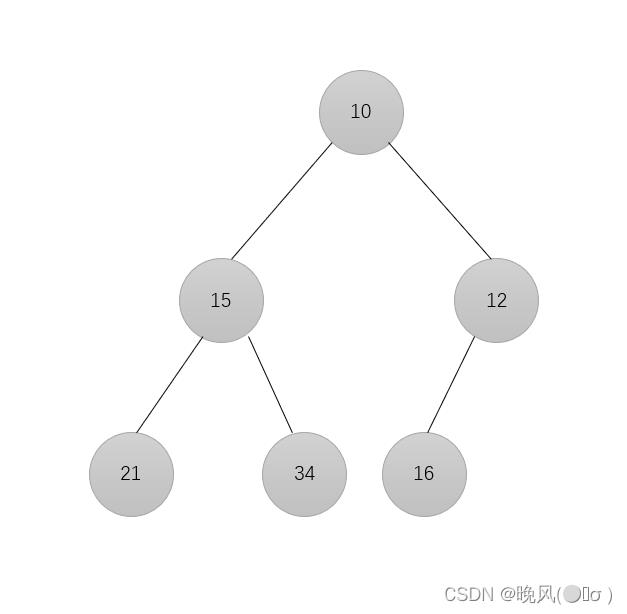
再与叶子结点16进行比较,不用交换,故共进行了三次比较。
四、总结
两种交换排序与前面的插入排序的总结如下表:
| 排序算法 | 空间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 排序方式 | 稳定性 | 适用性 |
|---|---|---|---|---|---|---|---|
| 直接插入排序 | O(1) | O(n2) | O(n) | O(n2) | 内部排序(In-place) | √ | 顺序存储和链式存储 |
| 折半插入排序 | O(1) | O(n2) | O(nlog2n) | O(n2) | 内部排序(In-place) | √ | 顺序存储 |
| 希尔排序 | O(1) | 依赖于增量序列 | 依赖于增量序列 | 依赖于增量序列 | 内部排序(In-place) | × | 顺序存储 |
| 冒泡排序 | O(1) | O(n2) | O(n) | O(n2) | 内部排序(In-place) | √ | 顺序存储和链式存储 |
| 简单选择排序 | O(1) | O(n2) | O(n2) | O(n2) | 内部排序(In-place) | × | 顺序存储和链式存储 |
| 快速排序 | 最好为O(log2n);最坏为O(n);平均情况下,为O(log2n) | O(nlog2n) | O(nlog2n) | O(n2) | 内部排序(In-place) | × | 顺序存储 |
| 堆排序 | O(1) | O(nlog2n) | O(nlog2n) | O(nlog2n) | 内部排序(In-place) | × | 顺序存储 |
以上是关于数据结构学习笔记——选择排序(简单选择排序和堆排序)的主要内容,如果未能解决你的问题,请参考以下文章