经典排序算法一从简单选择排序到堆排序的深度解析

Posted 2021-04-15 小鹿说开发那些事

一、简单选择排序

1、从一个简单问题谈起

给定待排序序列A[ 1.....n ]，选择出A中最小的记录。下面给出代码如下：

//选择待排序序列a中的最小记录,其下标为indexInt index = 0;for(int i=1;i<n;i++){ if(a[i]<a[index]) index=i; }

相信这段代码大家都能看懂，其中A[index]即为要找的最小记录。

2、简单选择排序的过程

问题描述：给定待排序序列A[ 1......n ] ，选择出第i小元素，并和A[i]交换，这就是一次简单选择排序。

//简单选择排序void SimpleSelectionSortOne(int *a,int n){ int i,j,index; //1.进行n-1趟选择，每次选出第i小记录 for(i=0;i<n-1;i++) { index=i; //2.选择第i小记录为a[index] for(j=i+1;j<n;j++) if(a[j]<a[index]) index=j; //3.与第i个记录交换 if(index!=i) {       a[i]=a[i]+a[index]; a[index]=a[i]-a[index]; a[i]=a[i]-a[index]; } }}

图解实例：

假设给定数组A[1......6]={ 2,5,7,9,5,2 }，我们来分析一下A数组进行选择排序的过程

第一趟：i=0，index=0， 不用交换。得到序列：{ 2,5,7,9,5,2 }

第二趟：i=1，index=5， a[1] 和 a[5] 进行交换。得到序列：{ 2,2,7,9,5,5 }

第三趟：i=2，index=4， a[2] 和 a[4] 进行交换交换。得到序列：{ 2,2,5,9,7,5 }

第四趟：i=3，index=5， a[3] 和 a[5] 进行交换交换。得到序列：{ 2,2,5,5,7,9 }

第五趟：i=4，index=5， 不用交换。得到序列：{ 2,2,5,5,7,9 }

第六趟：趟选择结束，得到有序序列：{ 1,2,3,5,8,9 }

最佳情况下（待排序序列有序）记录移动次数为0，最坏情况下（待排序序列逆序）记录移动次数n-1。外层循环进行了n-1趟选择，第i趟选择要进行n-i次比较。每一趟的时间：n-i次的比较时间+移动记录的时间（为一常数0或1，可以忽略）。总共进行了n-1趟。忽略移动记录的时间，所以总时间为(n-1)*(n-i)=n^2-(i+1)*n+i。时间复杂度为O（n^2）。不管是最坏还是最佳情况下，比较次数都是一样的，所以简单选择排序平均时间、最坏情况、最佳情况 时间复杂度都为O（n^2）。

递归实现简单选择排序

//递归函数进行简单选择排序void SimpleSelectionSortTwo(int *a,int n){ int index,i; if(n==0) return; //1.选择待排序序列a中的最小记录,其下标为index for(index=i=0;i<n;i++) { if(a[i]<a[index])         index=i; } //2.最小记录与待排序序列首元素进行交换 if(index!=0) { a[0]=a[0]+a[index]; a[index]=a[0]-a[index]; a[0]=a[0]-a[index];  } //3.待排序序列元素个数减少，递归对剩下的无序序列排序 simpleSelectionSortTwo(a+1,n-1);}

二、堆排序

从上文我们知道简单选择排序的时间复杂度为O（n^2），熟悉各种排序算法的朋友都知道，这个时间复杂度是很大的，所以怎样减小简单选择排序的时间复杂度呢？从上文分析中我们知道简单选择排序主要操作是进行关键字的比较，所以怎样减少比较次数就是改进的关键。 简单选择排序中第i趟需要进行n-i次比较，如果我们用到前面已排好的序列a[1...i-1]是否可以减少比较次数呢？答案是可以的。举个例子来说吧，A、B、C进行比赛，B战胜了A，C战胜了B，那么显然C可以战胜A，C和A就不用比了。

1、什么是堆

Min-heap: 父节点的值小于或等于子节点的值

Max-heap: 父节点的值大于或等于子节点的值

2、堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i–1)/2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

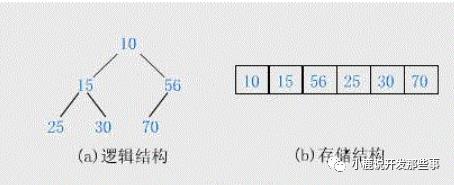
由于堆存储在下标从0开始计数的数组中，因此，在堆中给定下标为i的结点时：

（1）如果i=0，结点i是根结点，无父结点；否则结点i的父结点为结点(i-1)/2；

（2）如果2i+1>n-1，则结点i无左子女；否则结点i的左子女为结点2i+1；

（3）如果2i+2>n-1，则结点i无右子女；否则结点i的右子女为结点2i+2。

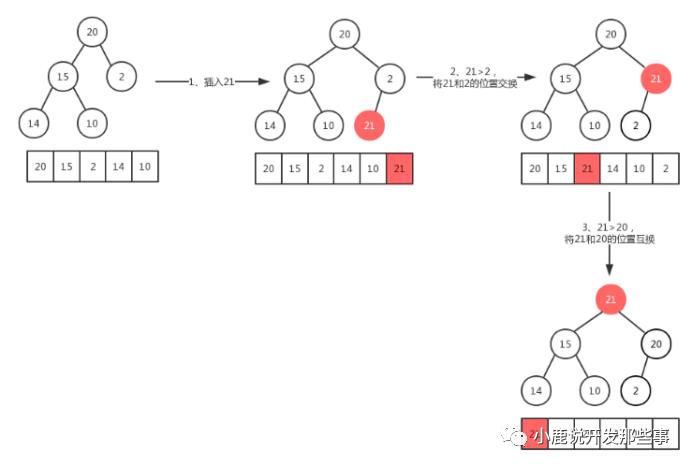
3、大根堆插入元素

插入一个元素：新元素被加入到heap的末尾，然后更新树以恢复堆的次序。

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。需要从下往上，与父节点的关键码进行比较，对调。

图解实例：

代码实例：

bool MaxHeap::Insert(const int iValue){ if(m_iCurrentHeapSize == m_iHeapMaxSize) {  cout<<"[info] max heap full"<<endl; return false; } 
 m_pHeap[m_iCurrentHeapSize] = iValue; ShiftUp(m_iCurrentHeapSize); m_iCurrentHeapSize++; return true;}

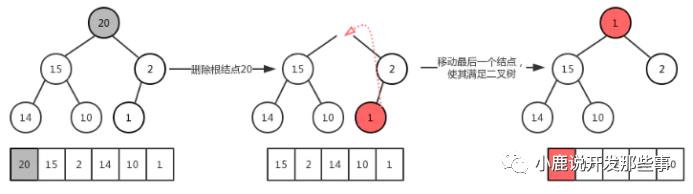
4、删除大根堆堆的最大元素

按定义，堆中每次都删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，堆的元素个数-1，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。

图解实例：

代码实例：

bool MaxHeap::RemoveMaxValue(int &iValue){ if(m_iCurrentHeapSize == 0) { cout<<"[info] max heap empty"<<endl; return false; }
 iValue = m_pHeap[0]; m_pHeap[0] = m_pHeap[m_iCurrentHeapSize-1]; m_iCurrentHeapSize--; ShiftDowm(0, m_iCurrentHeapSize-1); return true;}

5、创建最大堆

对于叶子节点，不用调整次序，根据满二叉树的性质，叶子节点比内部节点的个数多1.所以i=n/2 -1 ，不用从n开始。就是从最后一个有叶子结点的结点开始。

代码实例：

MaxHeap::MaxHeap(int *pArry,int iSize){ m_iHeapMaxSize = iSize > HEAPDEFAULTSIZE ? iSize : HEAPDEFAULTSIZE; try { m_pHeap = new int[m_iHeapMaxSize]; } catch(std::bad_alloc) { exit(-1); } m_iCurrentHeapSize = iSize; for(int i = 0; i < iSize; i++) { m_pHeap[i] = pArry[i]; }
 //craete max heap int iCurerentPos = (m_iCurrentHeapSize - 2)/2; while(iCurerentPos >= 0) { ShiftDowm(iCurerentPos, m_iHeapMaxSize-1); iCurerentPos--; }}

6、堆排序

过程描述：1、建堆  2、将堆顶记录和堆中最后一个记录交换  3、筛选法调整堆，堆中记录个数减少一个，重复第2步。整个过程中堆是在不断的缩减。

代码实现：

bool MaxHeap::HeapSort(){ if(m_iCurrentHeapSize == 0) { cout<<"[info] max heap is empty"<<endl; return false; }   for(int i=m_iCurrentHeapSize-1; i>0; i--) {  m_pHeap[0] = m_pHeap[0] + m_pHeap[i]; m_pHeap[i] = m_pHeap[0] - m_pHeap[i]; m_pHeap[0] = m_pHeap[0] - m_pHeap[i]; ShiftDowm(0, i - 1);  }  cout<<"[info] max heap sort content is: "<<endl; PrintHeap(); return true;}

三、编码测试

my_heap.h

/*@breif implement max heap@author wanglu@time 20200627*/#include<iostream>
const int HEAPDEFAULTSIZE = 50;class MaxHeap{ public: /* @brief build heap */ MaxHeap(int iSize = HEAPDEFAULTSIZE); MaxHeap(int *pArry,int iSize);  /* @brief insert into heap */ bool Insert(const int iValue);
 /*  @brief remvove max value */ bool RemoveMaxValue(int &iValue);
 /* @brief heap sotr  */ bool HeapSort();  /* @brief output heap elements */ void PrintHeap();
 /* @brief get max heap capacity */ int GetMaxCapacity(){ return m_iHeapMaxSize;  }
 /* @brief get current max heap size */ int GetCurrentSize(){ return m_iCurrentHeapSize;  }

 protected:
 /* @brief Adjust downward heap */ void ShiftDowm(int start, int end);
 /* @brief Upward adjustment heap */ void ShiftUp(int start); private: int *m_pHeap;//Max Heap object int m_iCurrentHeapSize;//heap current heap element size int m_iHeapMaxSize;//heap default max size
};

my_heap.cpp

#include<my_heap.h>#include<iostream>#include<stdlib.h>using namespace std;
MaxHeap::MaxHeap(int iSize){ m_iHeapMaxSize = iSize > HEAPDEFAULTSIZE ? iSize : HEAPDEFAULTSIZE; m_iCurrentHeapSize = 0; try { m_pHeap = new int[m_iHeapMaxSize]; } catch(std::bad_alloc) { exit(-1);  }}
MaxHeap::MaxHeap(int *pArry,int iSize){ m_iHeapMaxSize = iSize > HEAPDEFAULTSIZE ? iSize : HEAPDEFAULTSIZE; try { m_pHeap = new int[m_iHeapMaxSize];  } catch(std::bad_alloc) { exit(-1); } m_iCurrentHeapSize = iSize; for(int i = 0; i < iSize; i++) { m_pHeap[i] = pArry[i];  }  //craete max heap int iCurerentPos = (m_iCurrentHeapSize - 2)/2; while(iCurerentPos >= 0) { ShiftDowm(iCurerentPos, m_iHeapMaxSize-1); iCurerentPos--; }}
void MaxHeap::ShiftDowm(int start, int end){ int iCur = start; int iMaxChirdPos = 2*iCur + 1; int iTempValue = m_pHeap[iCur];
 while(iMaxChirdPos<= end) { if(iMaxChirdPos<end && m_pHeap[iMaxChirdPos]<m_pHeap[iMaxChirdPos+1]) { iMaxChirdPos++;  }
 if(m_pHeap[iCur] > m_pHeap[iMaxChirdPos]) { break; } else { m_pHeap[iCur] = m_pHeap[iMaxChirdPos]; m_pHeap[iMaxChirdPos] = iTempValue; iCur = iMaxChirdPos; iMaxChirdPos = 2*iCur + 1; } } m_pHeap[iCur] = iTempValue;}
bool MaxHeap::Insert(const int iValue){ if(m_iCurrentHeapSize == m_iHeapMaxSize) { cout<<"[info] max heap full"<<endl; return false; }
 m_pHeap[m_iCurrentHeapSize] = iValue; ShiftUp(m_iCurrentHeapSize); m_iCurrentHeapSize++; return true;}
void MaxHeap::ShiftUp(int start){ int iCur = start; int iParentPos = (iCur -1)/2; int itempValue = m_pHeap[iCur];  while(iCur > 0) { if(itempValue < m_pHeap[iParentPos]) { break; } else { m_pHeap[iCur] = m_pHeap[iParentPos]; m_pHeap[iParentPos] = itempValue; iCur = iParentPos; iParentPos = (iCur -1)/2; } } m_pHeap[iCur] = itempValue;}
bool MaxHeap::RemoveMaxValue(int &iValue){ if(m_iCurrentHeapSize == 0) { cout<<"[info] max heap empty"<<endl; return false; }
 iValue = m_pHeap[0]; m_pHeap[0] = m_pHeap[m_iCurrentHeapSize-1]; m_iCurrentHeapSize--; ShiftDowm(0, m_iCurrentHeapSize-1); return true;}
void MaxHeap::PrintHeap(){ for(int i=0; i<m_iCurrentHeapSize-1; i++) { cout<<m_pHeap[i]<<" ";  } cout<<m_pHeap[m_iCurrentHeapSize-1]<<endl;}bool MaxHeap::HeapSort(){  if(m_iCurrentHeapSize == 0) { cout<<"[info] max heap is empty"<<endl; return false;  }  for(int i=m_iCurrentHeapSize-1; i>0; i--) { m_pHeap[0] = m_pHeap[0] + m_pHeap[i]; m_pHeap[i] = m_pHeap[0] - m_pHeap[i]; m_pHeap[0] = m_pHeap[0] - m_pHeap[i]; ShiftDowm(0, i - 1); } cout<<"[info] max heap sort content is: "<<endl; PrintHeap(); return true;}

堆排序测试HeapSortTest.cpp

#include<iostream>#include<my_heap.h>using namespace std;


int main(){ int iArry[10] = {2,3,1,6,4,9,6,4,0,7}; MaxHeap MyHeap(iArry, 10); MyHeap.PrintHeap();    MyHeap.HeapSort(); return 0;}

堆排序打印如下：

堆插入测试HeapInsertTest.cpp

#include<iostream>#include<my_heap.h>using namespace std;


int main(){ int iArry[10] = {2,3,1,6,4,9,6,4,0,7}; MaxHeap MyHeap(iArry, 10); MyHeap.PrintHeap(); //MyHeap.HeapSort(); MyHeap.Insert(6); MyHeap.Insert(8); MyHeap.PrintHeap(); //int iValue; //MyHeap.RemoveMaxValue(iValue); //cout<<"[info] max heap remove max value is "<<iValue<<endl; //MyHeap.PrintHeap(); return 0;}

堆插入打印如下：

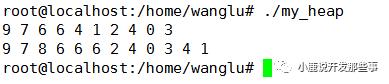
堆删除测试HeapRemoveTest.cpp

#include<iostream>#include<my_heap.h>using namespace std;


int main(){ int iArry[10] = {2,3,1,6,4,9,6,4,0,7}; MaxHeap MyHeap(iArry, 10); //MyHeap.PrintHeap(); //MyHeap.HeapSort(); MyHeap.Insert(6); MyHeap.Insert(8); MyHeap.PrintHeap(); int iValue; MyHeap.RemoveMaxValue(iValue); cout<<"[info] max heap remove max value is "<<iValue<<endl; MyHeap.PrintHeap(); return 0;}

堆删除最大元素打印如下：

创建最大堆测试CreateHeapTest.cpp

#include<iostream>#include<my_heap.h>using namespace std;


int main(){ int iArry[10] = {2,3,1,6,4,9,6,4,0,7}; MaxHeap MyHeap(iArry, 10); cout<<"[info] create max heap is:"<<endl; MyHeap.PrintHeap(); cout<<"[info] max heap max capacity is "<<MyHeap.GetMaxCapacity()<<endl; cout<<"[info] max heap current size is "<<MyHeap.GetCurrentSize()<<endl; return 0;}

创建最大堆打印如下：

四、时间复杂度分析

堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)...1]逐步递减，近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。