Java实现一致性Hash算法深入研究

Posted 2021-04-12 java新人交流

一致性Hash算法

关于一致性Hash算法，在我之前的博文中已经有多次提到了，MemCache超详细解读一文中”一致性Hash算法”部分，对于为什么要使用一致性Hash算法和一致性Hash算法的算法原理做了详细的解读。

算法的具体原理这里再次贴上：

先构造一个长度为2 32 的整数环（这个环被称为一致性Hash环），根据节点名称的Hash值（其分布为[0, 2 32 -1]）将服务器节点放置在这个Hash环上，然后根据数据的Key值计算得到其Hash值（其分布也为[0, 2 32 -1]），接着在Hash环上顺时针查找距离这个Key值的Hash值最近的服务器节点，完成Key到服务器的映射查找。

这种算法解决了普通余数Hash算法伸缩性差的问题，可以保证在上线、下线服务器的情况下尽量有多的请求命中原来路由到的服务器。

当然，万事不可能十全十美，一致性Hash算法比普通Hash算法更具有伸缩性，但是同时其算法实现也更为复杂，本文就来研究一下，如何利用Java代码实现一致性Hash算法。在开始之前，先对一致性Hash算法中的几个核心问题进行一些探究。

                            

数据结构的选取

一致性Hash算法最先要考虑的一个问题是：构造出一个长度为2 32 的整数环，根据节点名称的Hash值将服务器节点放置在这个Hash环上。

那么，整数环应该使用何种数据结构，才能使得运行时的时间复杂度最低？首先说明一点，关于时间复杂度， 常见的时间复杂度与时间效率的关系有如下的经验规则：

O(1) < O(log 2 N) < O(n) < O(N * log 2 N) < O(N 2 ) < O(N 3 ) < 2N < 3N < N!

一般来说，前四个效率比较高，中间两个差强人意，后三个比较差（只要N比较大，这个算法就动不了了）。OK，继续前面的话题，应该如何选取数据结构，我认为有以下几种可行的解决方案。

1、解决方案一：排序+List

我想到的第一种思路是：算出所有待加入数据结构的节点名称的Hash值放入一个数组中，然后使用某种排序算法将其从小到大进行排序，最后将排序后的数据放入List中，采用List而不是数组是为了结点的扩展考虑。

之后，待路由的结点，只需要在List中找到第一个Hash值比它大的服务器节点就可以了 ，比如服务器节点的Hash值是[0,2,4,6,8,10]，带路由的结点是7，只需要找到第一个比7大的整数，也就是8，就是我们最终需要路由过去的服务器节点。

如果暂时不考虑前面的排序，那么这种解决方案的时间复杂度：

（1）最好的情况是第一次就找到，时间复杂度为O(1)

（2）最坏的情况是最后一次才找到，时间复杂度为O(N)

平均下来时间复杂度为O(0.5N+0.5)，忽略首项系数和常数，时间复杂度为O(N)。

但是如果考虑到之前的排序，我在网上找了张图，提供了各种排序算法的时间复杂度：

看得出来，排序算法要么稳定但是时间复杂度高、要么时间复杂度低但不稳定，看起来最好的归并排序法的时间复杂度仍然有O(N * logN)，稍微耗费性能了一些。

2、解决方案二：遍历+List

既然排序操作比较耗性能，那么能不能不排序？可以的，所以进一步的，有了第二种解决方案。

解决方案使用List不变，不过可以采用遍历的方式：

（1）服务器节点不排序，其Hash值全部直接放入一个List中

（2）带路由的节点，算出其Hash值，由于指明了”顺时针”，因此遍历List，比待路由的节点Hash值大的算出差值并记录，比待路由节点Hash值小的忽略

（3）算出所有的差值之后，最小的那个，就是最终需要路由过去的节点

在这个算法中，看一下时间复杂度：

1、最好情况是只有一个服务器节点的Hash值大于带路由结点的Hash值，其时间复杂度是O(N)+O(1)=O(N+1)，忽略常数项，即O(N)

2、最坏情况是所有服务器节点的Hash值都大于带路由结点的Hash值，其时间复杂度是O(N)+O(N)=O(2N)，忽略首项系数，即O(N)

所以，总的时间复杂度就是O(N)。其实算法还能更改进一些：给一个位置变量X，如果新的差值比原差值小，X替换为新的位置，否则X不变。这样遍历就减少了一轮，不过经过改进后的算法时间复杂度仍为O(N)。

总而言之，这个解决方案和解决方案一相比，总体来看，似乎更好了一些。

3、解决方案三：二叉查找树

抛开List这种数据结构，另一种数据结构则是使用 二叉查找树 。对于树不是很清楚的朋友可以简单看一下这篇文章树形结构。

当然我们不能简单地使用二叉查找树，因为可能出现不平衡的情况。平衡二叉查找树有AVL树、红黑树等，这里使用红黑树，选用红黑树的原因有两点：

1、红黑树主要的作用是用于存储有序的数据，这其实和第一种解决方案的思路又不谋而合了，但是它的效率非常高

2、JDK里面提供了红黑树的代码实现TreeMap和TreeSet

另外，以TreeMap为例，TreeMap本身提供了一个tailMap(K fromKey)方法，支持从红黑树中查找比fromKey大的值的集合，但并不需要遍历整个数据结构。

使用红黑树，可以使得查找的时间复杂度降低为O(logN)，比上面两种解决方案，效率大大提升。

为了验证这个说法，我做了一次测试，从大量数据中查找第一个大于其中间值的那个数据，比如{{10000:0}}数据就找第一个大于5000的数据（模拟平均的情况）。看一下O(N)时间复杂度和O(logN)时间复杂度运行效率的对比：

	{{50000:0}}	{{100000:0}}	{{500000:0}}	{{1000000:0}}	{{4000000:0}}
ArrayList	1ms	1ms	4ms	4ms	5ms
LinkedList	4ms	7ms	11ms	13ms	17ms
TreeMap	0ms	0ms	0ms	0ms	0ms

因为再大就内存溢出了，所以只测试到{{4000000:0}}数据。可以看到，数据查找的效率，TreeMap是完胜的，其实再增大数据测试也是一样的，红黑树的数据结构决定了任何一个大于N的最小数据，它都只需要几次至几十次查找就可以查到。

当然，明确一点，有利必有弊，根据我另外一次测试得到的结论是， 为了维护红黑树，数据插入效率TreeMap在三种数据结构里面是最差的，且插入要慢上5~10倍 。

Hash值重新计算

服务器节点我们肯定用字符串来表示，比如”192.168.1.1″、”192.168.1.2″，根据字符串得到其Hash值，那么另外一个重要的问题就是 Hash值要重新计算，这个问题是我在测试String的hashCode()方法的时候发现的，不妨来看一下为什么要重新计算Hash值：

/**
 * String的hashCode()方法运算结果查看
 * @author 五月的仓颉 
 *
 */
public class StringHashCodeTest
{
    public static void main(String[] args)
    {
        System.out.println("192.168.0.0:111的哈希值：" + "192.168.0.0:1111".hashCode());
        System.out.println("192.168.0.1:111的哈希值：" + "192.168.0.1:1111".hashCode());
        System.out.println("192.168.0.2:111的哈希值：" + "192.168.0.2:1111".hashCode());
        System.out.println("192.168.0.3:111的哈希值：" + "192.168.0.3:1111".hashCode());
        System.out.println("192.168.0.4:111的哈希值：" + "192.168.0.4:1111".hashCode());
    }
}

我们在做集群的时候，集群点的IP以这种连续的形式存在是很正常的。看一下运行结果为：

192.168.0.0:111的哈希值：{{1845870087:0}}
192.168.0.1:111的哈希值：{{1874499238:0}}
192.168.0.2:111的哈希值：{{1903128389:0}}
192.168.0.3:111的哈希值：{{1931757540:0}}
192.168.0.4:111的哈希值：{{1960386691:0}}

这个就问题大了，[0,2 32 -1]的区间之中，5个HashCode值却只分布在这么小小的一个区间，什么概念？[0,2 32 -1]中有4294967296个数字，而我们的区间只有{{122516605:0}}，从概率学上讲这将导致97%待路由的服务器都被路由到”192.168.0.1″这个集群点上，简直是糟糕透了！

另外还有一个不好的地方：规定的区间是非负数，String的hashCode()方法却会产生负数（不信用”192.168.1.0:1111″试试看就知道了）。不过这个问题好解决，取绝对值就是一种解决的办法。

综上，String重写的hashCode()方法在一致性Hash算法中没有任何实用价值，得找个算法重新计算HashCode。这种重新计算Hash值的算法有很多，比如CRC32_HASH、FNV1_32_HASH、KETAMA_HASH等，其中KETAMA_HASH是默认的MemCache推荐的一致性Hash算法，用别的Hash算法也可以，比如FNV1_32_HASH算法的计算效率就会高一些。

一致性Hash算法实现版本1：不带虚拟节点

使用一致性Hash算法，尽管增强了系统的伸缩性，但是也有可能导致负载分布不均匀，解决办法就是使用 虚拟节点代替真实节点 ，第一个代码版本，先来个简单的，不带虚拟节点。

下面来看一下不带虚拟节点的一致性Hash算法的Java代码实现：

/**
 * 不带虚拟节点的一致性Hash算法
 * @author 五月的仓颉

可以运行一下看一下结果：

[192.168.0.0:111]加入集合中, 其Hash值为{{575774686:0}}
[192.168.0.1:111]加入集合中, 其Hash值为{{8518713:0}}
[192.168.0.2:111]加入集合中, 其Hash值为{{1361847097:0}}
[192.168.0.3:111]加入集合中, 其Hash值为{{1171828661:0}}
[192.168.0.4:111]加入集合中, 其Hash值为{{1764547046:0}}
[127.0.0.1:1111]的hash值为{{380278925:0}}, 被路由到结点[192.168.0.0:111]
[221.226.0.1:2222]的hash值为{{1493545632:0}}, 被路由到结点[192.168.0.4:111]
[10.211.0.1:3333]的hash值为{{1393836017:0}}, 被路由到结点[192.168.0.4:111]

看到经过FNV1_32_HASH算法重新计算过后的Hash值，就比原来String的hashCode()方法好多了。从运行结果来看，也没有问题，三个点路由到的都是顺时针离他们Hash值最近的那台服务器上。

使用虚拟节点来改善一致性Hash算法

上面的一致性Hash算法实现，可以在很大程度上解决很多分布式环境下不好的路由算法导致系统伸缩性差的问题，但是会带来另外一个问题：负载不均。

比如说有Hash环上有A、B、C三个服务器节点，分别有100个请求会被路由到相应服务器上。现在在A与B之间增加了一个节点D，这导致了原来会路由到B上的部分节点被路由到了D上，这样A、C上被路由到的请求明显多于B、D上的，原来三个服务器节点上均衡的负载被打破了。 某种程度上来说，这失去了负载均衡的意义，因为负载均衡的目的本身就是为了使得目标服务器均分所有的请求 。

解决这个问题的办法是引入虚拟节点，其工作原理是： 将一个物理节点拆分为多个虚拟节点，并且同一个物理节点的虚拟节点尽量均匀分布在Hash环上 。采取这样的方式，就可以有效地解决增加或减少节点时候的负载不均衡的问题。

至于一个物理节点应该拆分为多少虚拟节点，下面可以先看一张图：

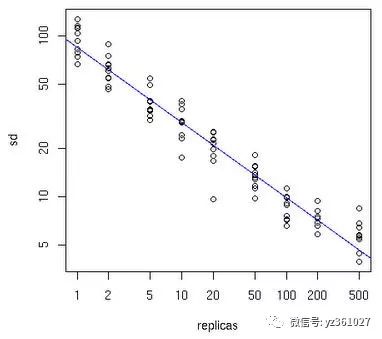
横轴表示需要为每台福利服务器扩展的虚拟节点倍数，纵轴表示的是实际物理服务器数。可以看出，物理服务器很少，需要更大的虚拟节点；反之物理服务器比较多，虚拟节点就可以少一些。比如有10台物理服务器，那么差不多需要为每台服务器增加100~200个虚拟节点才可以达到真正的负载均衡。

一致性Hash算法实现版本2：带虚拟节点

在理解了使用虚拟节点来改善一致性Hash算法的理论基础之后，就可以尝试开发代码了。编程方面需要考虑的问题是：

1、一个真实结点如何对应成为多个虚拟节点？

2、虚拟节点找到后如何还原为真实结点？

这两个问题其实有很多解决办法，我这里使用了一种简单的办法，给每个真实结点后面根据虚拟节点加上后缀再取Hash值，比如”192.168.0.0:111″就把它变成”192.168.0.0:111&&VN0″到”192.168.0.0:111&&VN4″，VN就是Virtual Node的缩写，还原的时候只需要从头截取字符串到”&&”的位置就可以了。

下面来看一下带虚拟节点的一致性Hash算法的Java代码实现：

关注一下运行结果：

从代码运行结果看，每个点路由到的服务器都是Hash值顺时针离它最近的那个服务器节点，没有任何问题。

通过采取虚拟节点的方法，一个真实结点不再固定在Hash换上的某个点，而是大量地分布在整个Hash环上，这样即使上线、下线服务器，也不会造成整体的负载不均衡。

后记

在写本文的时候，很多知识我也是边写边学，难免有很多写得不好、理解得不透彻的地方，而且代码整体也比较糙，未有考虑到可能的各种情况。抛砖引玉，一方面，写得不对的地方，还望网友朋友们指正；另一方面，后续我也将通过自己的工作、学习不断完善上面的代码。