我想知道运筹学中旅行背包问题。谢谢!
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了我想知道运筹学中旅行背包问题。谢谢!相关的知识,希望对你有一定的参考价值。
我想知道旅行商问题的数学求解过程。谢谢
参考技术A 背包问题是一个非常有名的问题。可以这样叙述如下。假设有 n 件物品,记为 d1,d2,d3,…… dn。对于每一种物品di (1=<i=<n), 它的重量是wi ,而它的价值为 vi。现在要求用这 n 种物品的子集填满背包,使其总重量不超过给定的重量限制 TOT,并使得背包的价值尽可能高。1.实数背包
物品可以一部分放在背包中,那么直接贪心就行了,把物品按性价比(v[i]/w[i])升序放入即为最优解。
复杂度O(n+nlogn)
2.整数背包
物品只能整个放入背包,不允许拆开放,用动态规划求解。
dp[i,j]表示前i个物品放入容量为j的背包中可以得到的最优解。
状态转移方程:dp[i,j]=maxdp[i-1,j],dp[i-1,j-w[i]]+v[i]
复杂度O(nm)
3.多重背包
与1、2不同,这里有k个背包,每个背包有不同的容量,其它一样。
没什么好办法,只能搜索。
对于每个物品i,枚举它能被放在背包j,也可以不放物品i。
复杂度O(kn)
可以针对不同的题目采取不同的剪枝。
背包问题数学模型为(由于输入问题,下标很难输入规范,如c1中1是下标,请注意)
maxZ=c1x1+c2x2+...+cnxn
w1x1+w2x2+...+wnxn<=W
xi>=0,且为整数,i=1,2,...,n
式中:
ck为第k种物品的单位价值,wk是第k种物品的单位重量或体积,W是背包的重量或体积限制。
动态规划的有关要素如下:
阶段k:第k次装载第k种物品(k=1,2,…,n)
状态变量sk:第k次装载时背包还可以装载的重量(或体积)
决策变量xk:第k次装载第k种物品的件数
决策允许集合:Dk(sk)=dk|0 xksk/wk,xk为整数
状态转移方程:sk+1=sk-wkxk
阶段指标:vk=ckxk
一般来说,用来解决背包问题的方法有递归法和贪心法等,但用这两中方法来解决背包问题都有其不可避免的缺点,递归法虽能遍历搜索空间,找到最优解,但由于此问题的解的空间是以2的N级增长的,所以它只适用于解决小规模的背包问题,而贪心法又很难真正找到最优解,此方法找到的最优解往往与真正的最优解相差很远。而遗传算法作为一种随机的优化与搜索方法,具有良好的并行性,而且遗传算法只需利用目标的取值信息,而无需递度等高价值信息,因此适用于任何规模。遗传算法的高度非线形的不连续多峰函数的优化以及无解析表达式的目标函数的优化,具有很强的通用性。
(如果你是需要计算机编程序的话,答案内容就更多些,现在不晓得你应用背包问题做什么呢) 参考技术B 8558 参考技术C ABCD
应用运筹学基础:组合优化 - 近似算法选讲
这节课介绍了斯坦纳树问题(Steiner tree)与旅行商问题(TSP),并讲解了它们的近似算法。
平面上的斯坦纳树
平面上的斯坦纳树指的是这样的问题:平面上有 $n$ 个点,要用总长尽量少的线段把它们连通起来。要注意,线段不一定要在给定的 $n$ 个点相交(不然跑个最小生成树就没了),完全可以在平面上的其它点相交。最优解中,线段在平面上除了给定点外的交点称为斯坦纳点。
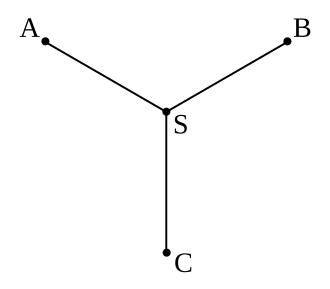

可以从上图看出 $n = 3$ 和 $n = 4$ 的情况,$S$、$S_1$ 和 $S_2$ 是斯坦纳点。$n = 3$ 时,斯坦纳点就是三角形的费马点。
平面上的斯坦纳树是一个 NP-Hard 问题。
满足三角不等式的完全图上的斯坦纳树
满足三角不等式的完全图上的斯坦纳树指的是这样的问题:给定一张满足三角不等式(对于任意两两有连边的三点 $x, y, z$,有 $w(x, y) \\le w(x, z) + w(z, y)$,$w$ 表示边权)的完全图 $G = (V, E)$ 和 $S \\subseteq V$,求 $G$ 的连通子图 $G\'$,使得 $S$ 中的所有点都在 $G\'$ 中,且 $G\'$ 边权之和最小。
即使有了这么多的限制条件,这个问题仍然是一个 NP-Hard 问题(证明见此)。下面我们提出它的一个 2- 近似算法:其实很简单,只要算出 $S$ 的最小生成树即可(别忘了是完全图,$S$ 肯定是连通的)。
算法近似比证明:
假设最优的斯坦纳树边权之和为 $\\text{OPT}$,最小生成树的边权之和为 $\\text{MST}$。我们把最优斯坦纳树中的每条边复制一次,得到一张有欧拉回路的图,它的边权总和为 $2\\text{OPT}$。
我们在欧拉图中任选一个 $S$ 中的点出发,找到一条欧拉回路 $L$。我们只走 $S$ 中的点,且每个点只走一次,如果不能沿着 $L$ 走到下一个点就直接“跳到”那个点(别忘了是完全图,这种“跳跃”称为 short-cutting)。

举个例子,例如上图是我们找到的欧拉回路的一部分,红色点是 $S$ 中的点。由于不能从第一个 a 沿着 $L$ 走到 $b$,我们要跳过去;由于 a 已经走过了,所以不能走 c → a → d,而是要从 c 直接跳到 d。
由于完全图符合三角不等式,直接跳过去肯定不比沿着 $L$ 走过去来得长。这样,我们就找到了 $S$ 的一个连通图,而且这个连通图的边权之和至多为 $2\\text{OPT}$。
别忘了,$S$ 的任何连通图,边权之和都不比最小生成树小。所以我们有 $\\text{MST} \\le 2\\text{OPT}$。这就证明了算法的近似比是 2。
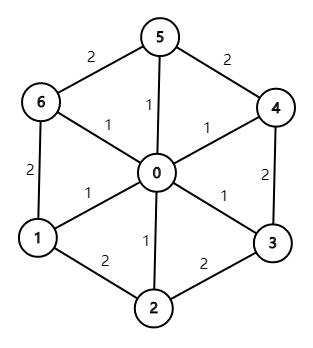
用上图的例子说明这个近似比对于这个算法是紧的。图中没有画出来的边权值都是 2。令 $S = \\{1, 2, \\dots, n\\}$,显然最优解为 $n$(利用中间的 0 作为斯坦纳点),但用上面的算法会得到 $2(n-1)$ 的结果,在 $n$ 足够大的时候近似比趋近于 2。
旅行商问题的近似比
大家都知道,完全图上的 TSP 是 NP-Hard。然而,完全图上的 TSP 甚至没有很好的近似比。下面证明完全图上的 TSP 不存在近似比为 $O(2^{\\text{poly}(n)})$ 的多项式算法,其中 $\\text{poly}(n)$ 表示 $n$ 的多项式。
我们利用哈密尔顿回路问题进行证明。对于普通无向图 $G = (V, E)$ 上的哈密尔顿回路问题,我们构造完全图 $G\' = (V, E\')$,$E\'$ 中一条边 $e\'$ 的边权 $w(e\')$ 定义如下:$$w(e\') = \\begin{cases} 1 & e\' \\in E \\\\ 2^{\\text{poly}(n)}n & e\' \\not\\in E \\end{cases}$$ 这张完全图的输入规模仍然是 $n$ 的多项式。
如果 TSP 存在近似比为 $O(2^{\\text{poly}(n)})$ 的算法,那么对于上面的完全图,算法就绝对不能选 $e\' \\not\\in E$ 的边。但如果算法只用 $e\' \\in E$ 的边构造出了一个解,那就同时找到了 $G$ 中的哈密尔顿回路。我们知道,找哈密尔顿回路本身就是 NPC 的,这就完成了证明。
满足三角不等式的完全图的旅行商问题
既然普通完全图上的旅行商问题这么难,我们给它加一点限制。在满足三角不等式的完全图上,TSP 就有很好的近似比。
首先容易证明这个问题近似比上界为 2:先跑个最小生成树(边权和肯定小等于最优哈密尔顿回路),把树上每条边重复一次变成欧拉图,在欧拉图上进行和斯坦纳树类似的 short-cutting 即可。
不过我们可以证明一个更紧的上界。不一定要把树上每条边都重复一次才能得到欧拉图嘛,如果我们把树上度数为奇数的点(下面简称奇点)进行配对(一张图的奇点肯定有偶数个,不用担心有一个匹配不上),每一对之间连一条边,那么构成的图就都是偶点,也就是一张欧拉图了。这种配对工作非常容易,只要用带花树什么的求一个最小权完美匹配即可。下面证明这种算法的近似比为 1.5。
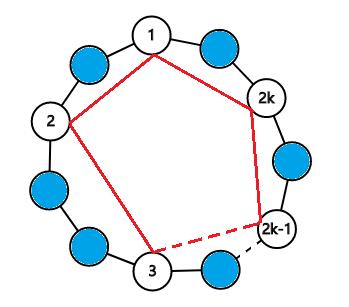
假设最优的哈密尔顿回路如上图,白色的点是最小生成树上的奇点。我们将奇点按顺序进行 short-cutting,就能得到两个不相交匹配(1 - 2, 3 - 4, ..., 2k-1 - 2k 以及 2 - 3, 4 - 5, ..., 2k - 1)。由于满足三角不等式,这两个匹配的权值之和肯定不大于 $\\text{OPT}$,那么两个匹配中较小的那个权值肯定不大于 $0.5\\text{OPT}$。别忘了,我们在算法中求出来的可是最小完美匹配,那么最小完美匹配的权值肯定也不大于 $0.5\\text{OPT}$。最小生成树 + 最小权完美匹配就证明了 1.5 的近似比。

上面的例子可以说明 1.5 对这个算法是紧的,没有画出来的边权值都是 2。右边实线是算法可能获得的最小生成树,虚线是算法可能算出的最小权完美匹配。显然最优解为 $n$,而算法可能得出的解是 $n + \\frac{n}{2}$。只要“梯形”上面的点足够多,那么近似比就是 1.5。
满足三角不等式的完全图的最短哈密尔顿路
下面来考虑一个有些不一样的问题:在满足三角不等式的完全图中,给定 $k = \\{0, 1, 2\\}$ 个固定点(即指定起点或者终点,或者都指定,或者都不指定),求满足固定点的最短哈密尔顿路。
这个问题可以通过以下近似算法解决:
1. 首先求个最小生成树 $T$;
2. 令点集 $S$ 包含两类点:在最小生成树上是偶点的固定点(因为要把固定点变奇点,才好找以它们开头的欧拉路),以及在最小生成树上是奇点的非固定点;
3. 类似于 TSP 问题,求个 $S$ 的最小权匹配 $M$,要求有 $2-k$ 个非固定点不匹配(只要加入 $2-k$ 个辅助点,与非固定点连权值为 0 的辅助边即可)。容易发现,这样会恰有 2 个点成为奇点,并且固定点一定在这 2 个点里;
4. 这样 $T \\cup M$ 就是一张有欧拉路的图,用 short-cutting 的方法把欧拉路变成哈密尔顿路即可。
这个算法在 $k \\in \\{0, 1\\}$ 时是 1.5 近似算法。下面进行证明。
$k = 0$
证明思想与 TSP 类似。假设最优解上有 $2t$ 个奇点,那么可以拆成两个匹配:1 - 2, 3 - 4, ..., (2t-3) - (2t-2)(2t-1 和 2t 没有匹配) 与 2 - 3, 4 - 5, 6 - 7, ..., (2t-2) - (2t-1)(1 和 2t 没有匹配),就可以证明 $M$ 的权值之和至多为 $0.5\\text{OPT}$。
$k = 1$
不妨设起点(设为 s)是固定点。
如果起点是奇点比较好办,假设最优解上有 $2t+1$ 个奇点(不含起点),那么可以拆成两个匹配:1 - 2, 3 - 4, ..., (2t-1) - 2t(2t+1 没有匹配)与 2 - 3, 4 - 5, ..., 2t - (2t+1)(1 没有匹配);
如果起点是偶点就比较麻烦了。假设最优解上有 $2t$ 个奇点,因为起点必须被匹配,我们没法把最优解拆成两个匹配符合要求的匹配。不过我们可以先把最优解拆成两个匹配 $M_1$:s - 1, 2 - 3, ..., (2t-2) - (2t-1)(2t 没有匹配),以及 $M_2$:1 - 2, 3 - 4, ..., (2t-1) - 2t(s 没有匹配)。
记 $w(M)$ 表示匹配 $M$ 的权重之和。如果 $w(M_1) < w(M_2)$ 那把 $M_1$ 并入 $T$ 答案就已经出来了,否则我们用 $T \\cup M_2$ 得到一张欧拉图,找出一条哈密尔顿回路,再去掉连接 s 的一条边,获得以 s 为起点的哈密尔顿路。由于 $w(M_2) \\le w(M_1)$,而我们加进图的是 $M_2$,所以仍然有 1.5 的近似比。
$k = 2$
$k = 2$ 的情况稍有不同,这个算法在同时给定起点与终点的情况下,近似比为 5/3。这次我们要把 $T \\cup \\text{OPT}$ 拆成 3 个匹配来完成证明。下面以起点(记为 s)与终点(记为 t)均为偶点为例进行证明,其它情况类似。
不难发现,$T - \\{s, t\\}$ 中有偶数个点,那么 $S$ 中也有偶数个点。设最优路径依次经过 $s, v_1, v_2, \\dots, v_{2k}, t$,其中 $v_i$ 是 $T$ 上的奇度点。
记 $u - v$ 表示仅通过最优路径中的边从点 $u$ 走到点 $v$,$u \\sim v$ 表示仅通过 $T$ 中的边从点 $u$ 走到点 $v$。我们尝试将 $T \\cup \\text{OPT}$ 拆成这样三个部分(不一定是匹配),且每条边至多使用一次:
1. $s - v_1, v_2 - v_3, \\dots, v_{2k-2} - v_{2k-1}, v_{2k} - t$;
2. $v_1 - v_2, v_3 - v_4, \\dots, v_{2k-1} - v_{2k}, s \\sim t$;
3. 找到 $s, t, v_1, v_2, \\dots, v_{2k}$ 的一个排列 $u_1, u_2, \\dots, u_{2k+2}$,$u_1 \\sim u_2, u_3 \\sim u_4, \\dots, u_{2k+1} \\sim u_{2k+2}$。
由于三角不等式,$u \\sim v$ 所使用的边的权值总和,一定大等于直接连接 $u$ 和 $v$ 的边的权值。如果我们能找到以上拆分,且每条边至多使用一次,那么我们就找到了 3 个 $S$ 的完美匹配,其权值总和不超过 $2\\text{OPT}$。这样,$S$ 的最小权完美匹配权值就不会超过 $\\frac{2}{3}\\text{OPT}$,就能证明 $\\frac{5}{3}$ 的近似比。
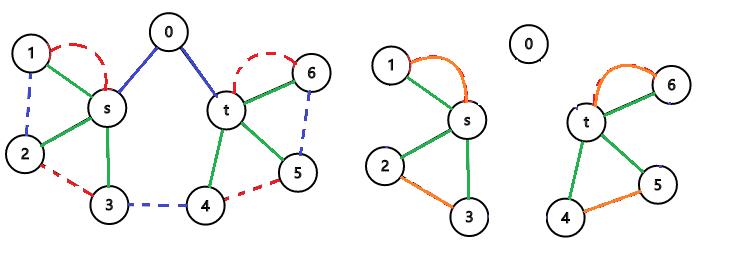
举个例子。左图中,实线是 $T$ 的边,虚线是 $\\text{OPT}$ 中的边;红边是部分 1 中的边,蓝边是部分 2 中的边,绿边是部分 3 中的边。
再看右图。虽然所有绿色边不能构成一个匹配,但是橙色边却可以构成一个匹配,而且权值之和一定不大于绿色边的权值之和。
很显然,部分 1 与部分 2 中除开 $s \\sim t$ 之外的边,就组成了最优路径。我们通过以下算法,在 $T$ 上找到部分 3 以及部分 2 中 $s \\sim t$ 中的边:
1. 在 $T$ 中找到从 $s$ 到 $t$ 的路径作为 $s \\sim t$,去掉使用过的边;
2. 对于每个连通块,选择任意一个奇度点 $u$,在 $T$ 中找到通往另一个奇度点 $v$ 的路径,且路径上不含其它奇度点。去掉使用过的边;
3. 重复步骤 2,直到 $S$ 中的点都在步骤 2 中找到了对应的点。
根据算法描述容易看出,如果算法成功退出,我们就找到了需要的拆分。接下来说明 $S$ 中的每个点都能在步骤 2 中找到对应的点,即算法可以成功退出。
注意到 $s$ 与 $t$ 均为偶度点。步骤 1 结束后,由于 $s$ 与 $t$ 是路径端点,去掉路径上的边后,$s$ 与 $t$ 都变成了奇度点;而路径上的其它点在去掉路径上的边后,奇偶性不变。
步骤 2 中,由于每个连通块一定有偶数个奇度点,所以一定可以找到符合要求的 $u$ 和 $v$。由于路径中间不含其它奇度点,所以其它点的奇偶性不变,不影响算法的后续运行;而 $u$ 与 $v$ 作为路径端点,在去掉路径中的边后都变成了偶度点,不会再次被选中,也不影响算法的后续运行。
因此,我们一定可以将 $T \\cup \\text{OPT}$ 拆成 $S$ 的 3 个完美匹配,即可证明算法的近似比不超过 $\\frac{5}{3}$。
以上是关于我想知道运筹学中旅行背包问题。谢谢!的主要内容,如果未能解决你的问题,请参考以下文章