如何用MATLAB编写双线性变换法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何用MATLAB编写双线性变换法相关的知识,希望对你有一定的参考价值。
参考技术A wp1=0.3*pi;wp2=0.6*pi;ws1=0.4*pi;ws2=0.5*pi;Ap=3;As=10;Fs=1;B=ws2-ws1;w0=sqrt(ws1*ws2);
wp=max(abs(wp1),abs(wp2));ws=1;
[N,wc]=buttord(wp,ws,Ap,As,'s');
[num,den]=butter(N,wc,'s');
[numt,dent]=lp2bs(num,den,w0,B);
[numd,dend]=bilinear(numt,dent,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
norm=max(abs(h));
numd=numd/norm;
subplot(2,2,1);
plot(w/pi,20*log(abs(h)/norm));grid;
xlabel('Butterworth BS DF');
ylabel('Gain,dB');
wp1=0.3*pi;wp2=0.6*pi;ws1=0.4*pi;ws2=0.5*pi;Ap=3;As=10;Fs=1;
B=ws2-ws1;w0=sqrt(ws1*ws2);
wp=max(abs(wp1),abs(wp2));ws=1;
[N,wc]=cheb1ord(wp,ws,Ap,As,'s');
[num,den]=cheby1(N,Ap,wc,'s');
[numt,dent]=lp2bs(num,den,w0,B);
[numd,dend]=bilinear(numt,dent,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
norm=max(abs(h));
numd=numd/norm;
subplot(2,2,2);
plot(w/pi,20*log(abs(h)/norm));grid;
xlabel('ChebyshevI BS DF');
ylabel('Gain,dB');
wp1=0.3*pi;wp2=0.6*pi;ws1=0.4*pi;ws2=0.5*pi;Ap=3;As=10;Fs=1;
B=ws2-ws1;w0=sqrt(ws1*ws2);
wp=max(abs(wp1),abs(wp2));ws=1;
[N,wc]=cheb2ord(wp,ws,Ap,As,'s');
[num,den]=cheby2(N,As,wc,'s');
[numt,dent]=lp2bs(num,den,w0,B);
[numd,dend]=bilinear(numt,dent,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
norm=max(abs(h));
numd=numd/norm;
subplot(2,2,3);
plot(w/pi,20*log(abs(h)/norm));grid;
xlabel('ChebyshevII BS DF');
ylabel('Gain,dB');
wp1=0.3*pi;wp2=0.6*pi;ws1=0.4*pi;ws2=0.5*pi;Ap=3;As=10;Fs=1;
B=ws2-ws1;w0=sqrt(ws1*ws2);
wp=max(abs(wp1),abs(wp2));ws=1;
[N,wc]=ellipord(wp,ws,Ap,As,'s');
[num,den]=ellip(N,Ap,As,wc,'s');
[numt,dent]=lp2bs(num,den,w0,B);
[numd,dend]=bilinear(numt,dent,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
norm=max(abs(h));
numd=numd/norm;
subplot(2,2,4);
plot(w/pi,20*log(abs(h)/norm));grid;
xlabel('Tuoyuan BS DF');
ylabel('Gain,dB');
计算机图像处理之形状变换
图像形状变换
图像的形状变换主要是指图像的 缩小、 放大与 错切。
图像的形状变换通常在目标物识别中使用
图像比例缩放
将图像进行全比例变换
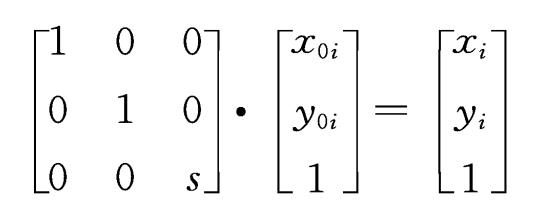
图像比例缩放变换
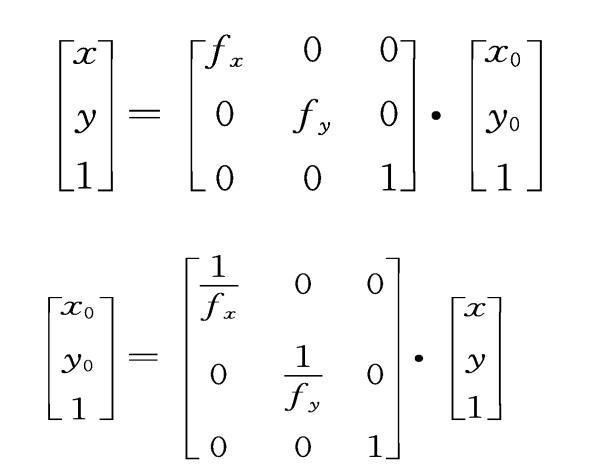
图像比例缩放是指将给定的图像比例缩放图像在x轴方向按比例缩放fx倍, 在y轴方向按比例缩放fy倍,从而获得一幅新的图像。
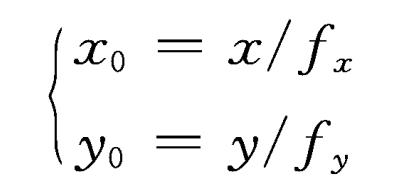
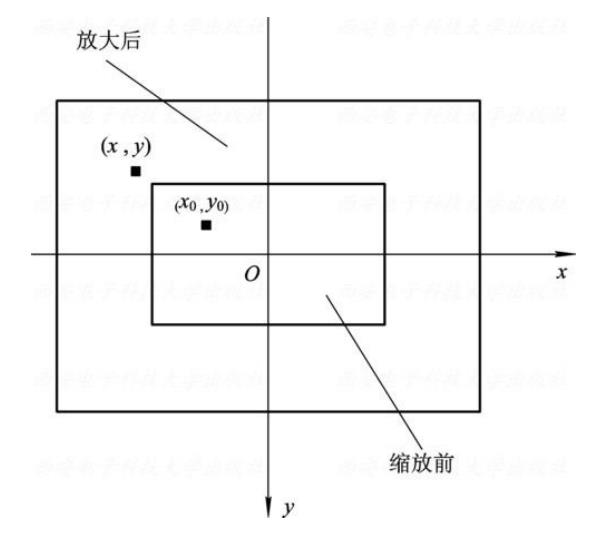
比例缩放后图像中的像素在原图像中可能找不到对应的像素点, 则此时需要进行插值处理。(常用的两种插值处理方法: 一种是直接赋值为与它最相近的像素值的最近邻域法; 另一种是双线性内插法。)
图像缩小变换
分为按比例缩小和不按比例缩小两种。
图像缩小之后,因为承载的信息量小了,所以画布可相应缩小。

图像缩小的实现方法
图像缩小实际上就是对原有的多个数据进行挑选或处理,获得期望缩小尺寸的数据,并且尽量保持原有的特征不丢失。最简单的方法就是等间隔地选取数据。
图像的比例缩小

按任意比例缩小
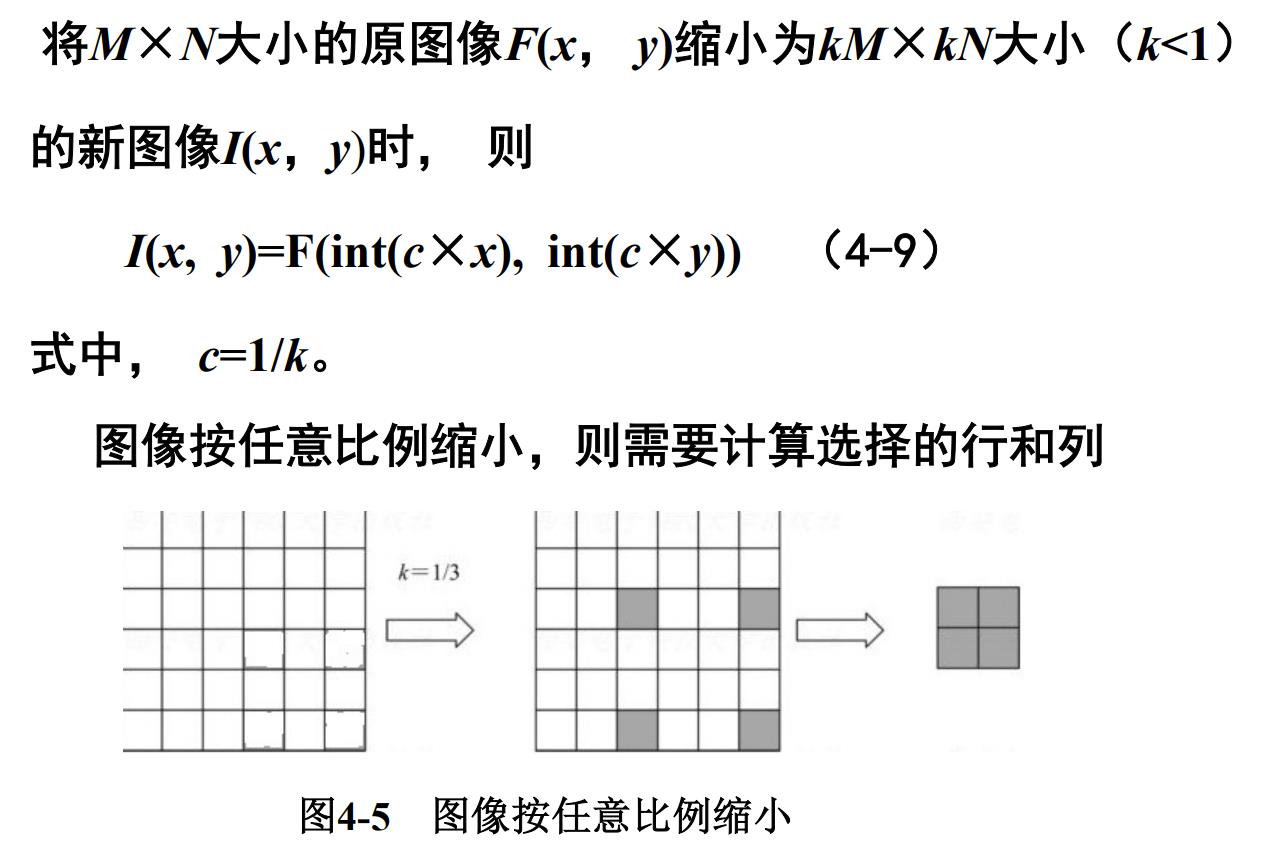
图像非比例缩小
在x和y方向的缩小比例不同, 一定会产生图像的几何畸变。
方法:


图像缩小例题
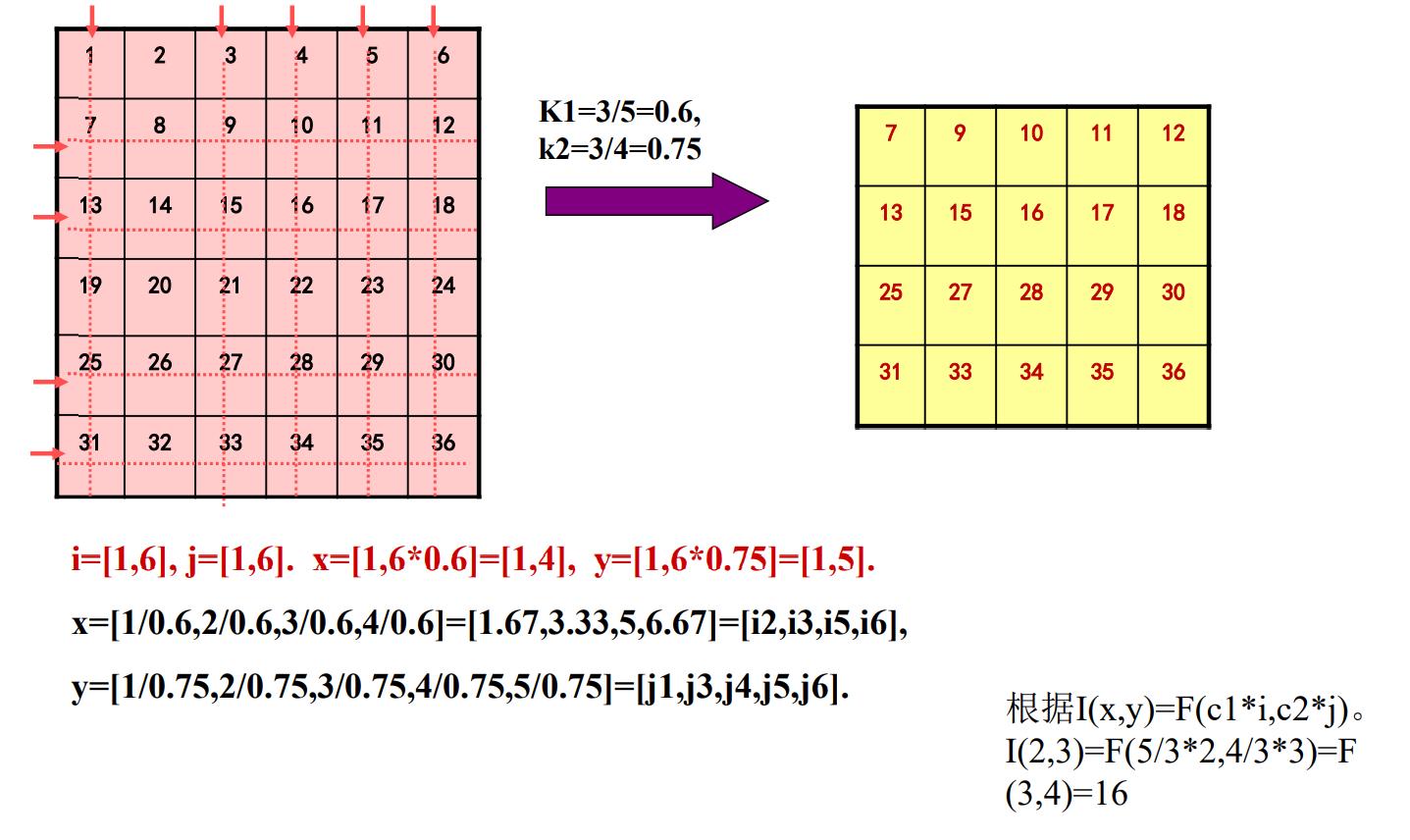
图像放大变换
图像缩小是从多信息中选出需要的信息,而图像放大则是需要对多出的空位填入适当的值,是信息的估计问题,所以较图像的缩小要困难。
利用相邻像素相关性来实现图像的放大。与图像缩小相同,按比例放大不会引起图像的畸变,而不按比例放大则会产生图像的畸变,图像放大一般采用最近邻域法和线性插值法。
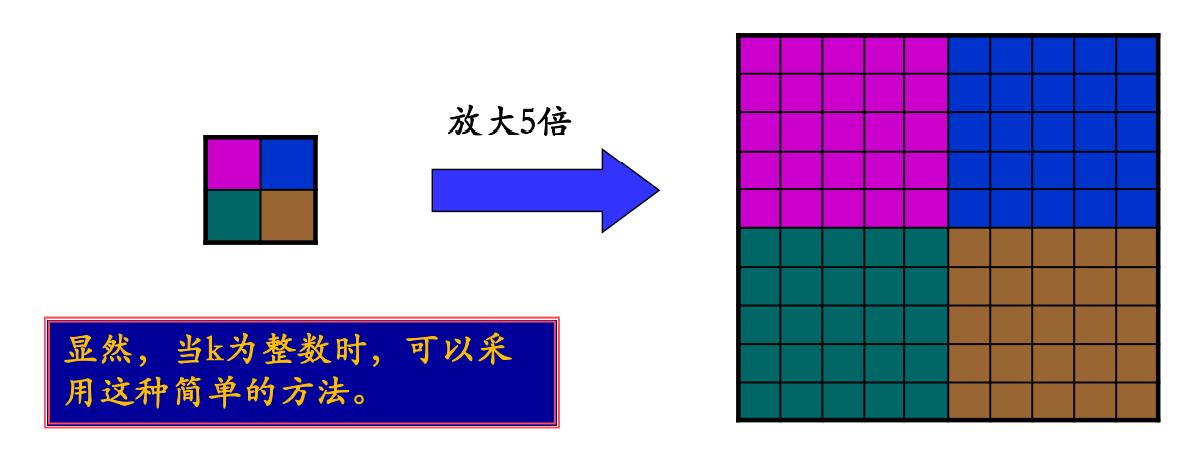
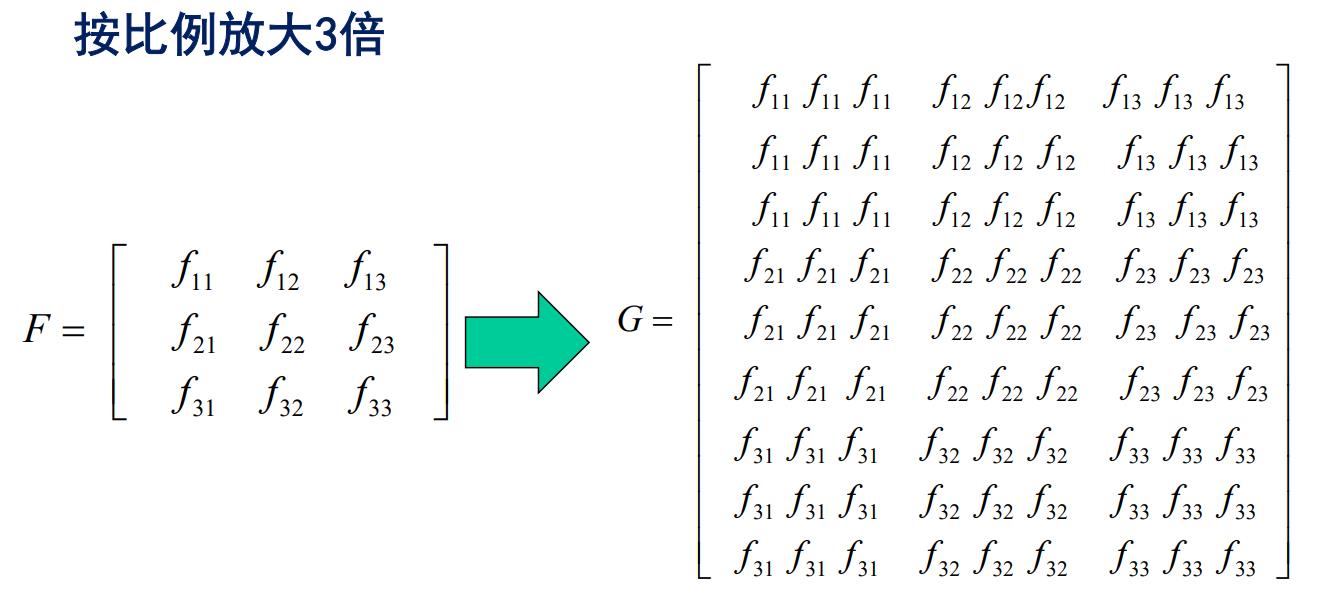
最近邻域法
最简单的思想是,如果需要将原图像放大为k倍,则将原图像中的每个像素值,填在新图像中对应的k*k大小的子块中。
图像非比例放大
在x和y方向的放大比例不同, 一定会产生图像的几何畸变。
方法:


如果比例放大倍数k×k太大,按照前面的最近邻方法处理会出现马赛克效应。
线性插值法
为了提高几何变换后的图像质量,常采用线性插值法。该方法的原理是,当求出的分数地址与像素点不一致时,求出周围四个像素点的距离比,根据该比率, 由四个邻域的像素灰度值进行线性插值。
双线性插值
为什么进行插值
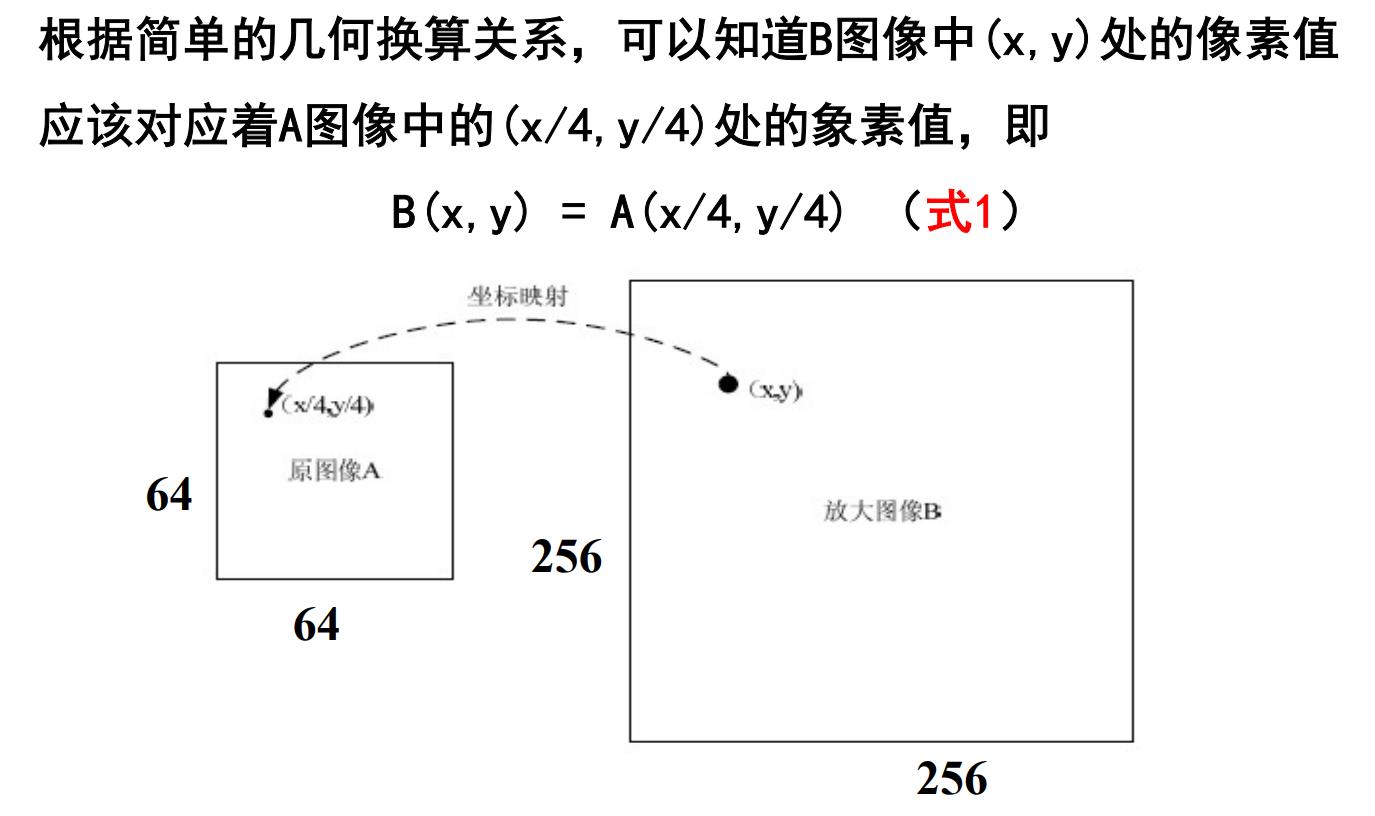
对于B中的点:(4,4),(4,8),(4,16)…(256,256)这些位置,通过式1就可以计算出其在A中的位置,从而可以得到灰度值。
对于B中的点: (1,1),(1,2),(1,3)…等等这些坐标点而言,按照式1计算,那么它们在A中对应的坐标不再是整数。比如,B(1,1)对应A(0.25,0.25)。
对于数字图像而言,小数坐标是没有意义的。因此,必须考虑采用某种方法来得到B中像素点在A中对应位置上的灰度级。 为此,引入了插值
插值的引入
处理非整数坐标问题的方法被称为图像灰度级插值。
常用的插值方式有三种:最近邻域插值、双线性插值、双三次插值。
效果上,最近邻域插值<双线性插值<双三次插值。
双线性插值的原理
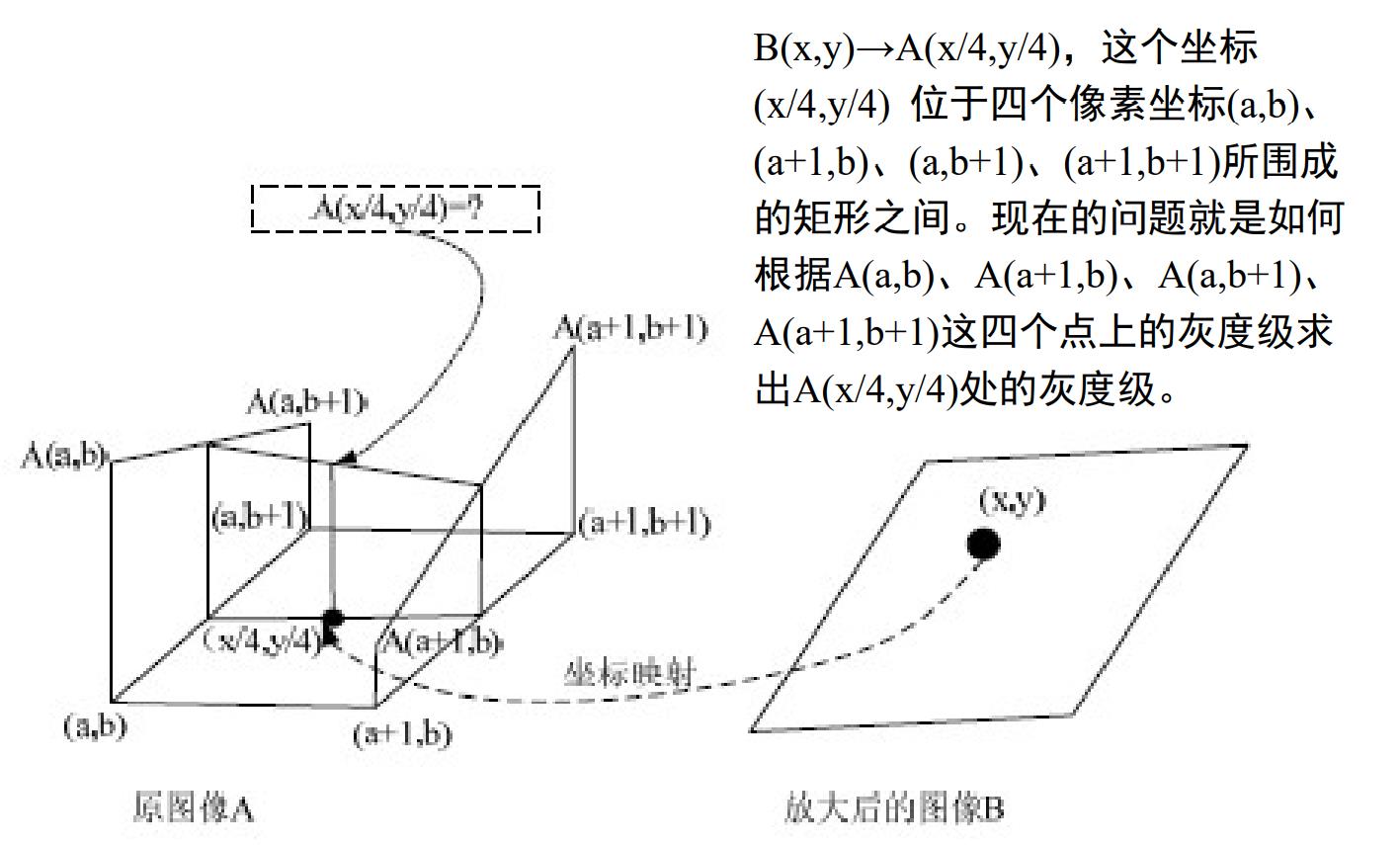
基本假设:灰度级在纵横方向上都是线性变化的。双线性插值
方法:双线性插值也称作一阶插值,先沿图像的每一列(行)进行线性插值,再对插值后的图像矩阵沿着行(列)方向进行线性插值。坐标(x,y)处插值前后的灰度值分别记为f(x,y)和g(x,y)
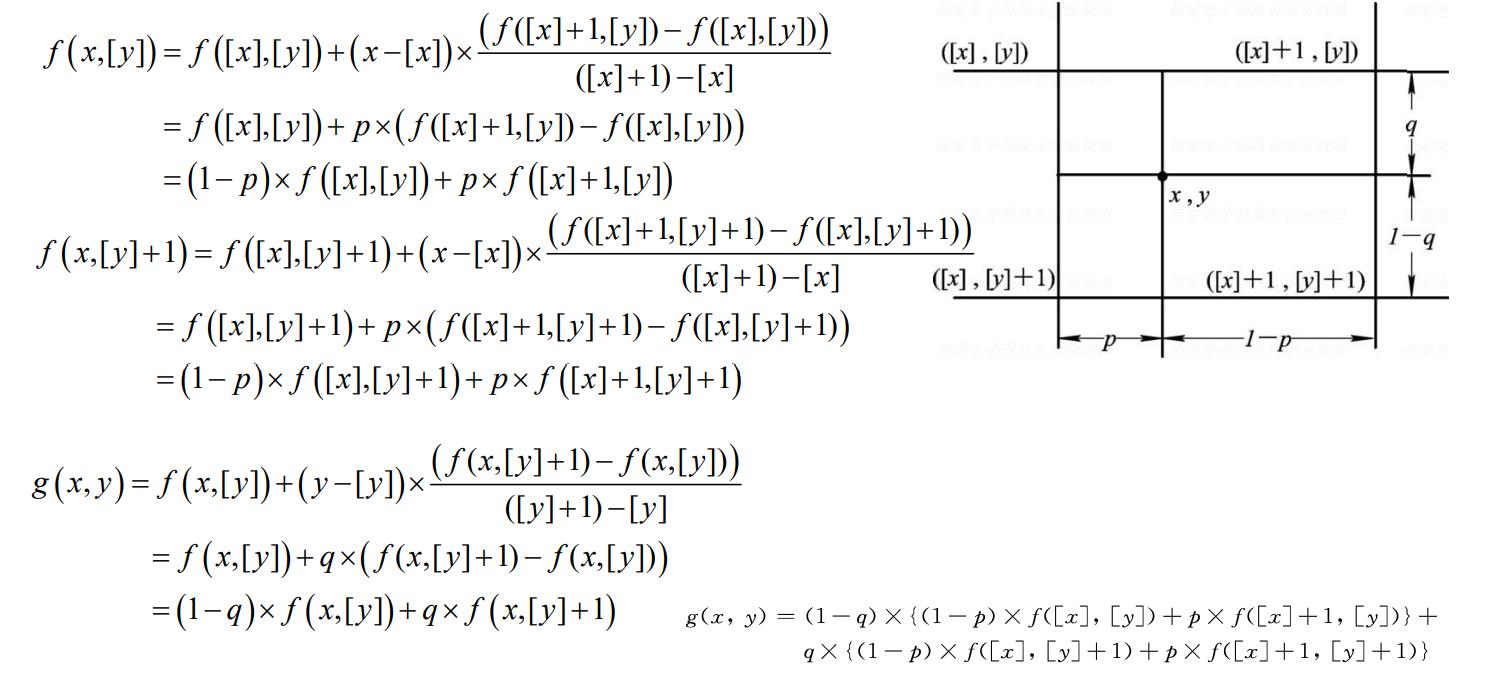

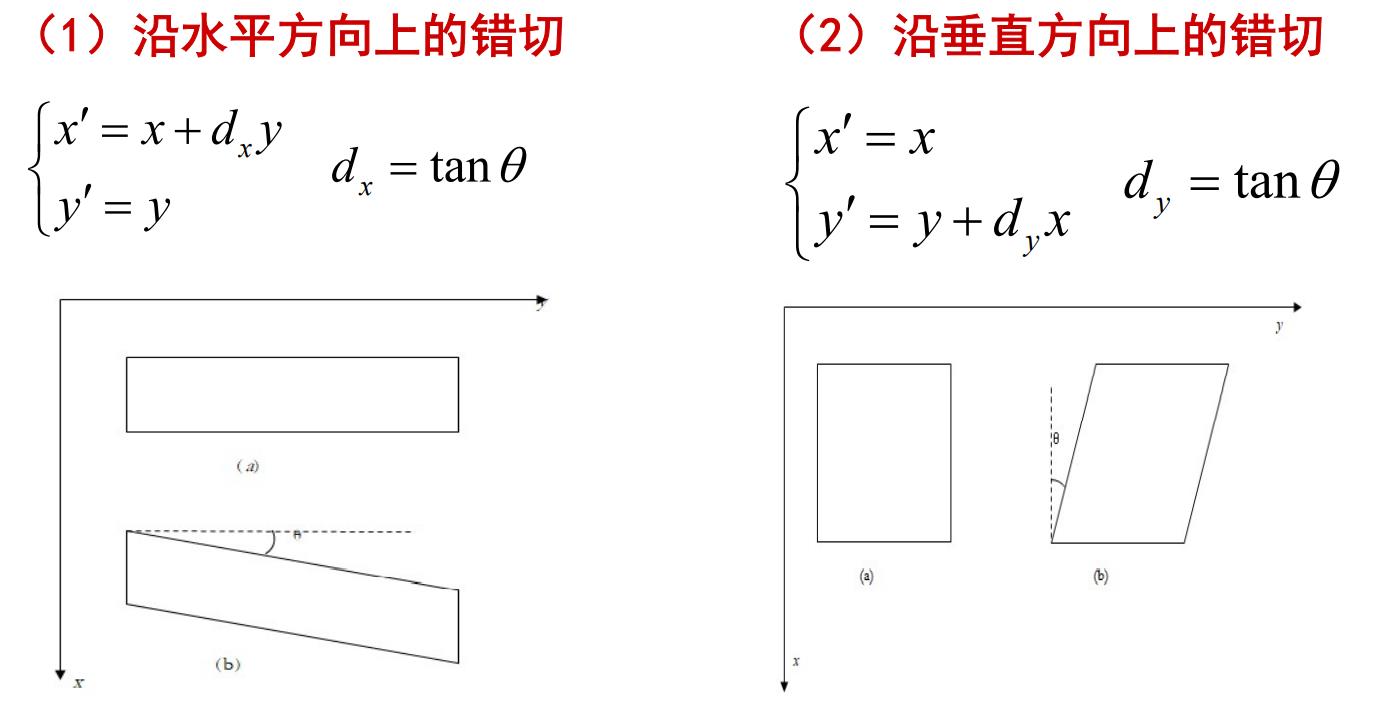
图像的错切变换
因为绝大多数图像都是三维物体在二维平面上的投影得到的,所以需要研究图像的错切现象。
图像的错切变换实际上是平面景物在投影平面上的非垂直投影。
错切使图像中的图形产生扭变,这种扭变只在一个方向上产生,即分别称为水平方向错切或垂直方向错切。
图像错切变换例—垂直方向
I=imread('lena.bmp');
I=double(I);
H=size(I);
B=zeros(H(1)+round(H(2)*tan(pi/6)),H(2),H(3));
for a=1:H(1)
for b=1:H(2)
B(a+round(b*tan(pi/6)),b,1:H(3))=I(a,b,1:H(3));
end
End
imshow(uint8(B));

图像错切变换例—水平方向
I=imread('lena.bmp');
I=double(I);
H=size(I);
B1=zeros(H(1),H(2)+round(H(1)*tan(pi/6)),H(3));
for a=1:H(1)
for b=1:H(2)
B1(a,b+round(a*tan(pi/6)),1:H(3))=I(a,b,1:H(3));
end
end
imshow(uint8(B1));

课后作业
按照式(4-8), 自行编写一个实现图像比例缩放的函数。
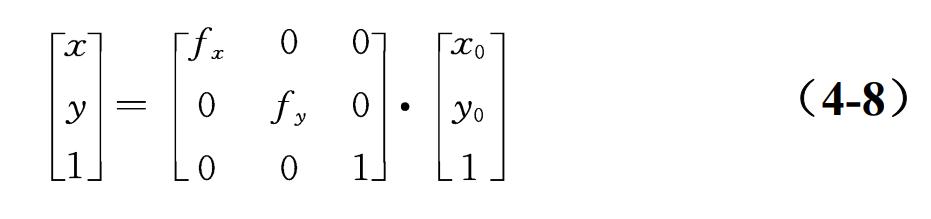
在OpenCV中也提供了进行图像比例缩放的函数resize,其格式为resize(src, dst, dst_size)
对目标图像需要进行插值处理, 常用的插值方法有最近邻插值法、 双线性插值法、 像素关系重采样法和立方插值法等, 其中默认的插值方法为双线性插值法。
以上是关于如何用MATLAB编写双线性变换法的主要内容,如果未能解决你的问题,请参考以下文章