深度优先搜索和广度优先搜索

Posted 2021-04-11 Hollis

点击上方“Hollis”关注我，精彩内容第一时间呈现。

全文字数：   3000

阅读时间：  10分钟

图的应用很广泛，也有很多非常有用的算法，当然也有很多待解决的问题，根据性质，图可以分为无向图和有向图。

图

之所以要研究图，是因为图在生活中应用比较广泛：

图是若干个顶点(Vertices)和边(Edges)相互连接组成的。边仅由两个顶点连接，并且没有方向的图称为无向图。 在研究图之前，有一些定义需要明确，下图中表示了图的一些基本属性的含义，这里就不多说明。

 

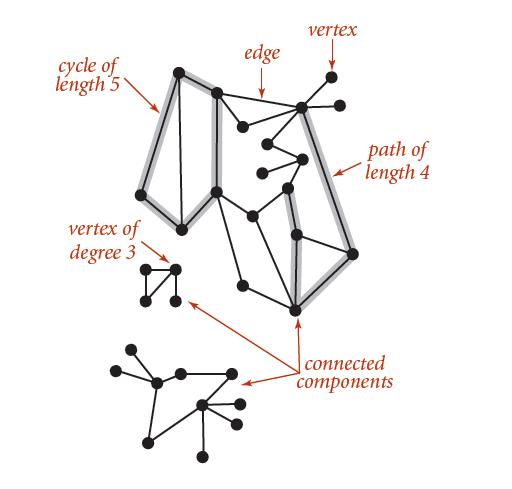
在研究图之前，我们需要选用适当的数据结构来表示图，有时候，我们常被我们的直觉欺骗,如下图，这两个其实是一样的，这其实也是一个研究问题，就是如何判断图的形态。

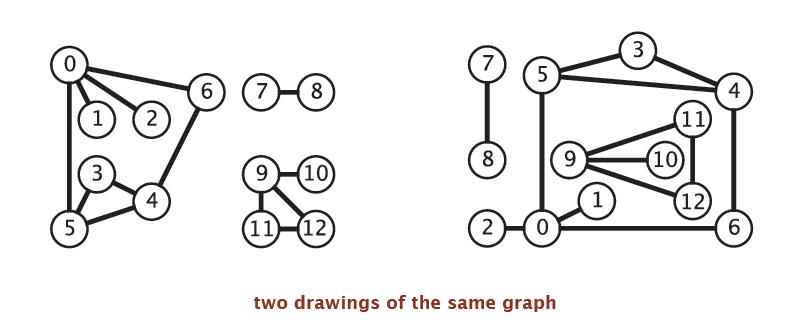
要用计算机处理图，我们可以抽象出以下的表示图的API：

Graph的API的实现可以由多种不同的数据结构来表示，最基本的是维护一系列边的集合，如下：

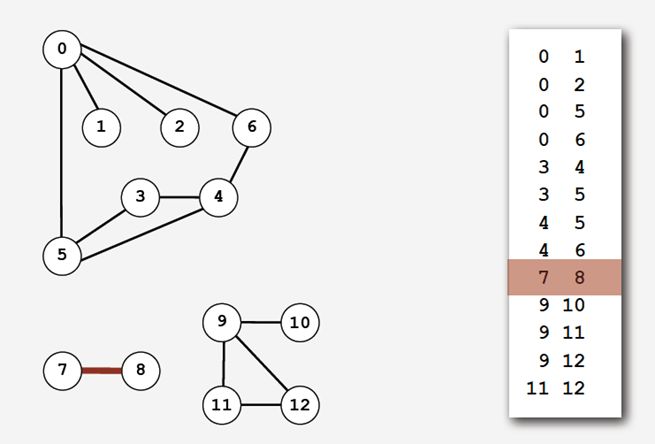
还可以使用邻接矩阵来表示：

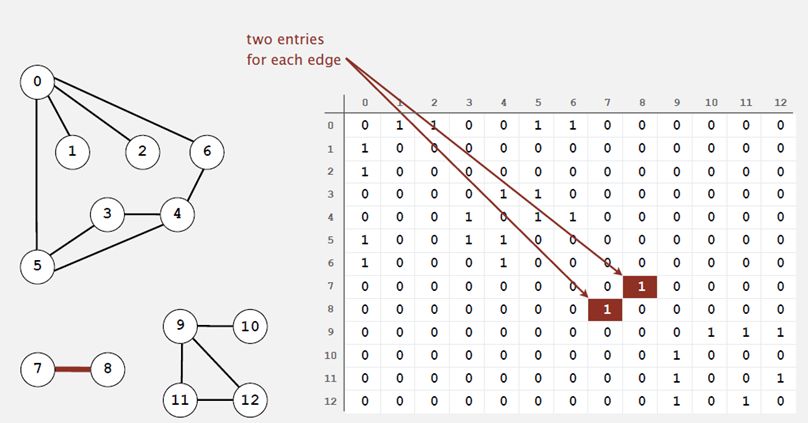
也可以使用邻接列表来表示：

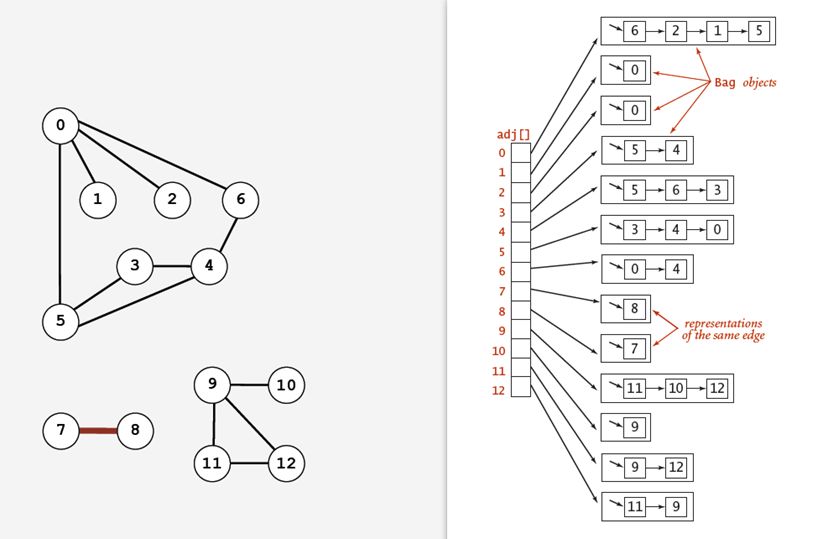
由于采用如上方式具有比较好的灵活性，采用邻接列表来表示的话，可以定义如下数据结构来表示一个Graph对象。

public class Graph
{
   private readonly int verticals;//顶点个数
   private int edges;//边的个数
   private List<int>[] adjacency;//顶点联接列表

   public Graph(int vertical)
   {
       this.verticals = vertical;
       this.edges = 0;
       adjacency=new List<int>[vertical];
       for (int v = 0; v < vertical; v++)
       {
           adjacency[v]=new List<int>();
       }
   }

   public int GetVerticals ()
   {
       return verticals;
   }

   public int GetEdges()
   {
       return edges;
   }

   public void AddEdge(int verticalStart, int verticalEnd)
   {
       adjacency[verticalStart].Add(verticalEnd);
       adjacency[verticalEnd].Add(verticalStart);
       edges++;
   }

   public List<int> GetAdjacency(int vetical)
   {
       return adjacency[vetical];
   }
}

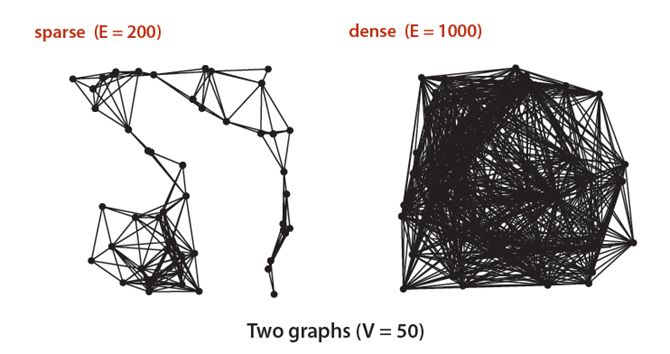
图也分为稀疏图和稠密图两种，如下图：

在这两个图中，顶点个数均为50，但是稀疏图中只有200个边，稠密图中有1000个边。在现实生活中，大部分都是稀疏图，即顶点很多，但是顶点的平均度比较小。

 

采用以上三种表示方式的效率如下：

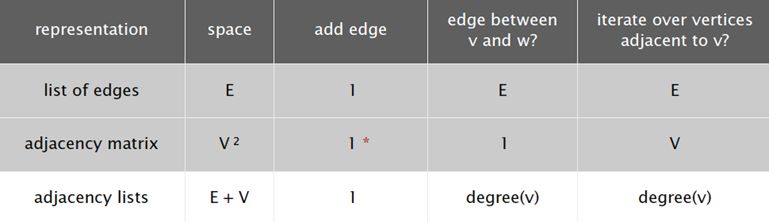
在讨论完图的表示之后，我们来看下在图中比较重要的一种算法，即深度优先算法。

深度优先算法

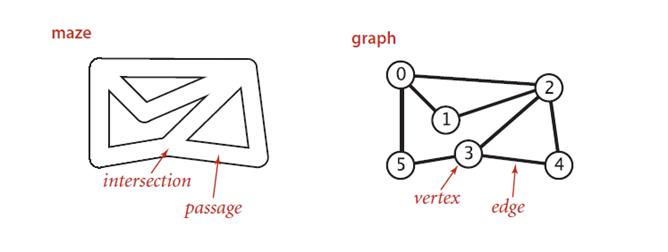
在谈论深度优先算法之前，我们可以先看看迷宫探索问题。下面是一个迷宫和图之间的对应关系：

迷宫中的每一个交会点代表图中的一个顶点，每一条通道对应一个边。

迷宫探索可以采用Trémaux绳索探索法。即：

• 在身后放一个绳子

• 访问到的每一个地方放一个绳索标记访问到的交会点和通道

• 当遇到已经访问过的地方，沿着绳索回退到之前没有访问过的地方：

  
  

图示如下：

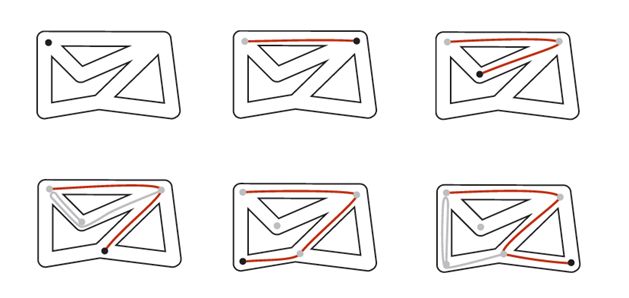
下面是迷宫探索的一个小动画：

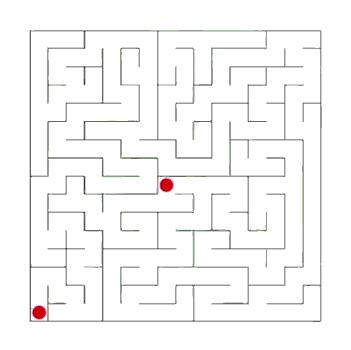
深度优先搜索算法模拟迷宫探索。在实际的图处理算法中，我们通常将图的表示和图的处理逻辑分开来。所以算法的整体设计模式如下：

• 创建一个Graph对象

• 将Graph对象传给图算法处理对象，如一个Paths对象

• 然后查询处理后的结果来获取信息

下面是深度优先的基本代码，我们可以看到，递归调用dfs方法，在调用之前判断该节点是否已经被访问过。

public class DepthFirstSearch
{
   private bool[] marked;//记录顶点是否被标记
   private int count;//记录查找次数

   private DepthFirstSearch(Graph g, int v)
   {
       marked = new bool[g.GetVerticals()];
       dfs(g, v);
   }

   private void dfs(Graph g, int v)
   {
       marked[v] = true;
       count++;
       foreach (int vertical in g.GetAdjacency(v))
       {
           if (!marked[vertical])
               dfs(g,vertical);
       }
   }

   public bool IsMarked(int vertical)
   {
       return marked[vertical];
   }

   public int Count()
   {
       return count;
   }
}

试验一个算法最简单的办法是找一个简单的例子来实现。

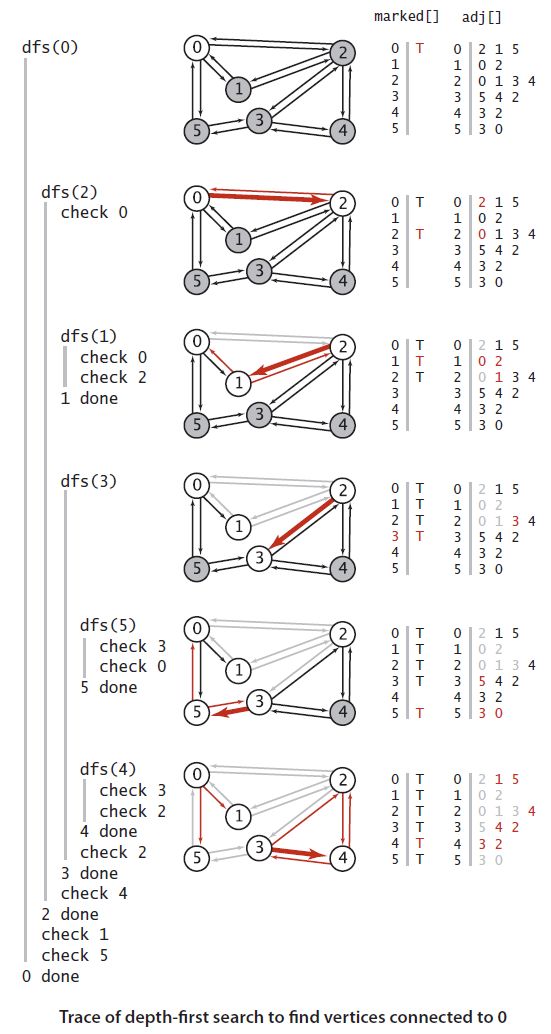
有了这个基础，我们可以实现基于深度优先的路径查询，要实现路径查询，我们必须定义一个变量来记录所探索到的路径。

所以在上面的基础上定义一个edgesTo变量来后向记录所有到s的顶点的记录，和仅记录从当前节点到起始节点不同，我们记录图中的每一个节点到开始节点的路径。为了完成这一日任务，通过设置edgesTo[w]=v，我们记录从v到w的边，换句话说，v-w是做后一条从s到达w的边。 edgesTo[]其实是一个指向其父节点的树。

public class DepthFirstPaths
{
   private bool[] marked;//记录是否被dfs访问过
   private int[] edgesTo;//记录最后一个到当前节点的顶点
   private int s;//搜索的起始点

   public DepthFirstPaths(Graph g, int s)
   {
       marked = new bool[g.GetVerticals()];
       edgesTo = new int[g.GetVerticals()];
       this.s = s;
       dfs(g, s);
   }

   private void dfs(Graph g, int v)
   {
       marked[v] = true;
       foreach (int w in g.GetAdjacency(v))
       {
           if (!marked[w])
           {
               edgesTo[w] = v;
               dfs(g,w);
           }
       }
   }

   public bool HasPathTo(int v)
   {
       return marked[v];
   }

   public Stack<int> PathTo(int v)
   {

       if (!HasPathTo(v)) return null;
       Stack<int> path = new Stack<int>();

       for (int x = v; x!=s; x=edgesTo[x])
       {
           path.Push(x);
       }
       path.Push(s);
       return path;
   }
}

 

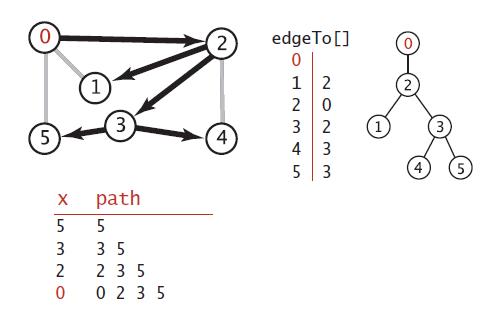
上图中是黑色线条表示 深度优先搜索中，所有定点到原点0的路径， 他是通过edgeTo[]这个变量记录的，可以从右边可以看出，他其实是一颗树，树根即是原点，每个子节点到树根的路径即是从原点到该子节点的路径。

下图是深度优先搜索算法的一个简单例子的追踪。 

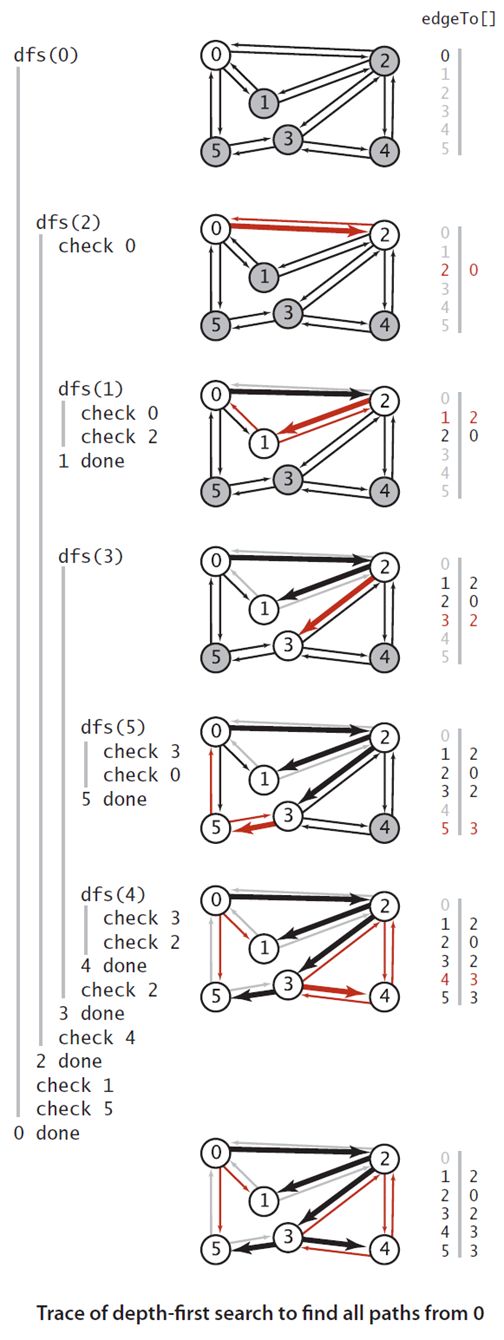
通常我们更关注的是一类单源最短路径的问题，那就是给定一个图和一个源S，是否存在一条从s到给定定点v的路径，如果存在，找出最短的那条(这里最短定义为边的条数最小)

深度优先算法是将未被访问的节点放到一个堆中(stack)，虽然在上面的代码中没有明确在代码中写stack，但是 递归 间接的利用递归堆实现了这一原理。

 广度优先算法

和深度优先算法不同， 广度优先是将所有未被访问的节点放到了队列中。其主要原理是：

• 将 s放到FIFO中，并且将s标记为已访问

• 重复直到队列为空

  
  

1. 移除最近最近添加的顶点v

2. 将v未被访问的节点添加到队列中

3. 标记他们为已经访问

   
   

广度优先是以距离递增的方式来搜索路径的。

class BreadthFirstSearch
{
   private bool[] marked;
   private int[] edgeTo;
   private int sourceVetical;//Source vertical

   public BreadthFirstSearch(Graph g, int s)
   {
       marked=new bool[g.GetVerticals()];
       edgeTo=new int[g.GetVerticals()];
       this.sourceVetical = s;
       bfs(g, s);
   }

   private void bfs(Graph g, int s)
   {
       Queue<int> queue = new Queue<int>();
       marked[s] = true;
       queue.Enqueue(s);
       while (queue.Count()!=0)
       {
           int v = queue.Dequeue();
           foreach (int w in g.GetAdjacency(v))
           {
               if (!marked[w])
               {
                   edgeTo[w] = v;
                   marked[w] = true;
                   queue.Enqueue(w);
               }
           }
       }
   }

   public bool HasPathTo(int v)
   {
       return marked[v];
   }

   public Stack<int> PathTo(int v)
   {
       if (!HasPathTo(v)) return null;

       Stack<int> path = new Stack<int>();
       for (int x = v; x!=sourceVetical; x=edgeTo[x])
       {
           path.Push(x);
       }
       path.Push(sourceVetical);
       return path;
   }

}

广度优先算法的搜索步骤如下：

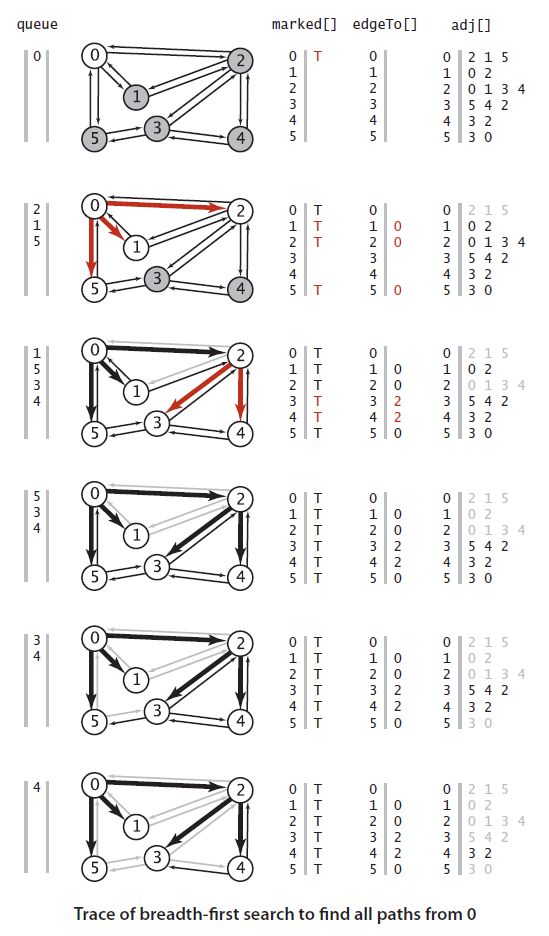
广度优先搜索首先是在距离起始点为1的范围内的所有邻接点中查找有没有到达目标结点的对象，如果没有，继续前进在距离起始点为2的范围内查找，依次向前推进。

本文简要介绍了无向图中的深度优先和广度优先算法，这两种算法时图处理算法中的最基础算法，也是后续更复杂算法的基础。其中图的表示，图算法与表示的分离这种思想在后续的算法介绍中会一直沿用，下文将讲解无向图中深度优先和广度优先的应用，以及利用这两种基本算法解决实际问题的应用。

- MORE | 更多精彩文章 -

• 
  

如果你看到了这里，说明你喜欢本文。

那么请长按二维码，关注Hollis