#14 二分查找（Binary Search）

Posted 2021-04-10 码字Plus

二分查找是时间复杂度为O(log n)的搜索算法中较为高效的算法之一，这一点和在平衡的二叉搜索树中搜索元素的时间复杂度相当。在使用二分查找之前，有两个条件需要预先满足：

•集合必须是在恒定的时间内执行索引操作，意味着集合必须是RandomAccessCollection类型的；•集合必须是sorted的。

Example

在Swift标准库中的Array结构中，通过index(of:)来实现线性的元素搜索，也就是意味着Array中的元素搜索需要遍历整个数组。

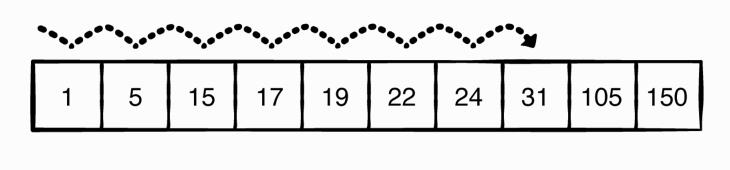
而二分查找则是在已排序的数组上，以不同的处理方式进行元素的搜索。例如下图所示，在已排序的数组中搜索元素31：

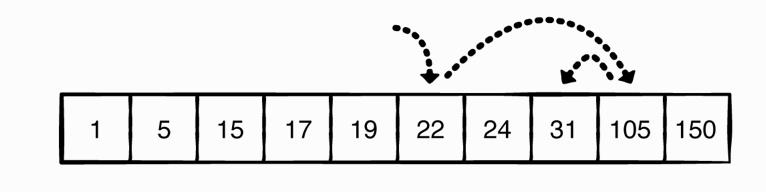
和一般的数组元素查找不同的是，二分查找按照如下的步骤进行元素的搜索：

Step 1：找到中间位置的索引

二分查找第一步，便是找到集合中间位置，这一步非常直接，通过集合的元素总数进行计算获得：

Step 2：检查中间索引位置的元素

下一步则是检查中间位置的元素，如果和预检索的元素匹配，则直接返回索引，如果不相符，则继续第三步，继续检索元素。

Step 3：递归进行二分查找

最后一步是递归调用二分查找，但是这时，仅仅需要检索的是集合中间索引左侧或者右侧，而非整个集合。当中间位置的元素小于预检索的元素时，则检索中间位置右侧，反之，检索中间位置左侧。

二分查找每一步的检索之后，都会减少一半的检索范围，这样大大的减小了检索的时间耗时，提高检索效率。

在上述例子中，为了检索元素31，由于中间位置的元素为22，小于预检索的元素31，因此将继续检索中间位置元素22的右侧元素：

二分查找从大的方面来说，每一次的元素检索只需要三步，直到无法将集合再次进行左右划分或者找到元素为止。

二分查找的时间复杂度为O(log n)。

算法实现

首先定义二分查找使用范围，以及集合元素的可比较性：

public extension RandomAccessCollection where Element: Comparable { func binarySearch(for value: Element, in range: Range<Index>? = nil) -> Index? {
 }}

•由于二分查找仅仅适用于集合类型RandomAccessCollection，并且其中的元素需要可比较的特性，因此针对该类型进行扩展并设定元素可比较性，并添加二分查找方法的定义；•二分查找在运行过程中需要递归调用，因此在函数定义中要执行每一次递归的范围，参数range是可选类型，在首次进行二分查找的时候，不需要传入range，故其默认值为nil。

public extension RandomAccessCollection where Element: Comparable { func binarySearch(for value: Element, in range: Range<Index>? = nil) -> Index?{
 let range = range ?? startIndex ..< endIndex
 guard range.lowerBound < range.upperBound else { return nil }
 let size = distance(from: range.lowerBound, to: range.upperBound) let middle = index(range.lowerBound, offsetBy: size / 2)
 if self[middle] == value { return middle } else if self[middle] > value { return binarySearch(for: value, in: range.lowerBound ..< middle) } else { return binarySearch(for: value, in: middle ..< range.upperBound) } }}

•首先检查range是否为nil，如果为nil，则获取集合完整的索引范围startIndex ..< endIndex；•检查集合是否为空，这里的检查方式是通过集合的最小边界和最大边界进行判断集合是否至少有一个元素，否则直接返回nil；•通过集合的最小边界和最大边界，获取集合的长度，之后使用index(offsetBy:)方法获取集合中间位置的索引；•如果中间位置的元素就是我们要查找的元素，则直接返回中间位置索引；•如果中间位置的元素大于预查找的元素，则说明预查找元素在集合中间位置的左侧，递归调用binarySearch(for:range:)方法，继续查找；•如果中间位置的元素小于预查找的元素，则说明预查找的元素在集合中间位置的右侧，递归调用binarySearch(for:range:)方法，继续查找。

example(of: "binary search") { let array = [1, 5, 15, 17, 19, 22, 24, 31, 105, 150]
 let search31 = array.firstIndex(of: 31) let binarySearch31 = array.binarySearch(for: 31)
 print("index(of:): (String(describing: search31))") print("binarySearch(of:): (String(describing: binarySearch31))")}
/*---Example of binary search---index(of:): Optional(7)binarySearch(of:): Optional(7)*/

二分查找是一种强大的算法，每当某些场景下，集合的元素时已排序的情况下，都可以考虑使用二分查找的方法。另外，如果遇到的问题似乎进行元素搜索需要O(n^2)的时间复杂度，可以考虑先对集合进行前期的排序，然后采用二分查找的方法将时间复杂度降低到O(n log n)的程度。

关键点总结

•二分查找仅仅对已排序的集合有效；•有时候，对集合进行排序后，再使用二分查找是有益的；•对于集合本身，其sorted方法的时间复杂度为O(n)，而二分查找的时间复杂度为O(log n)，对于大型数据集合来说，二分查找的可伸缩性更好。

二分查找思想典型的应用场景就是在Bug原因的追查上面，当面对一个无从知晓其最终的引发点的时候，可以尝试使用二分查找的思想，分段校验代码的执行结果，逐步缩小Bug追查的范围，提高Bug原因的追查效率等。