写写代码系列028：二叉树的深度优先遍历

Posted 2021-04-09 阿尔法放荡不羁

题目描述

写出二叉树的深度优先先序遍历，中序遍历和后序遍历。

题目解析

二叉树是每一个节点最多有两个子节点的树，也是最常用的树的结构，一般面试里边出现的都是二叉树。举个例子，下面这个树就是二叉树：

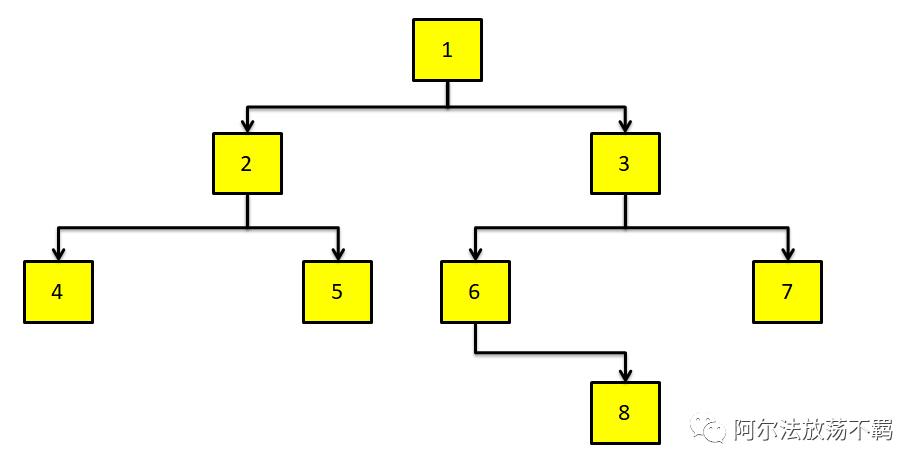
每一个节点要么有两个子节点，要么有一个子节点，要么没有子节点。没有子节点的节点叫做叶子节点，有子节点的节点叫做根节点。本例中根节点有1 2 3 6四个，叶子节点是4 5 8 7这四个。

对于这个树，最开始是1,1的左边是2，1的右边是3；2的左边是4，2的右边是5；4的左右都是None，5的左右都是None；3的左边是6，3的右边是7；6的左边是None，6的右边是8；8的左右都是None，7的左右都是None。我们先用程序写一下这个树的结构。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

对于树的遍历，大类有两种，深度优先和广度优先，今天写深度优先。

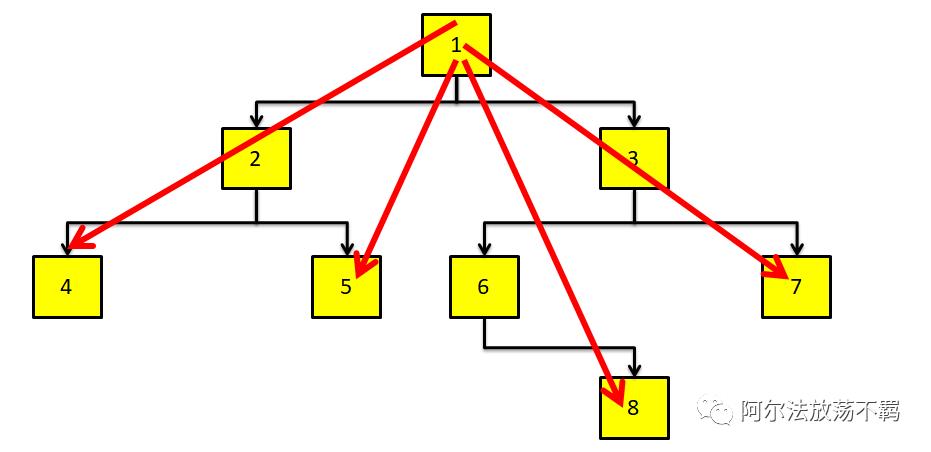
深度优先是先往深了找，也就是竖着找，对于上面的例子，就是先找124，然后5，然后368，然后7，大概是下图这样的一个顺序。

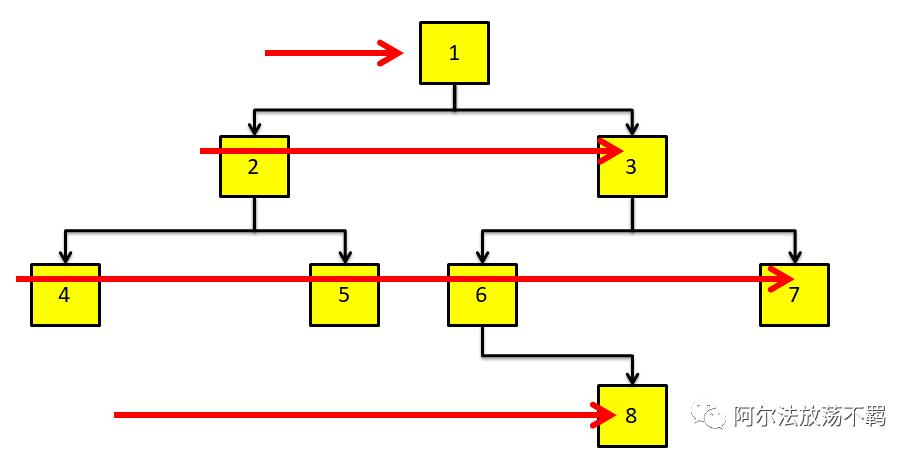
广度优先是横着找，大概是下图这样的一个顺序。

深度优先又分为三种情况：1.先序遍历  2.中序遍历  3.后序遍历。

1、先序遍历。先序遍历是指，对于树，先遍历该树的根节点，然后是左子树，然后是右子树。对于本例来说，顺序就是1 2 4 5 3 6 8 7。

2、中序遍历。中序遍历是指，对于树，先遍历该树的左子树，然后是根节点，然后是右子树。对于本例来说，顺序就是4 2 5 1 6 8 3 7。

3、后序遍历。后序遍历是指，对于树，先遍历该树的左子树，然后是右子树，然后是根节点。对于本例来说，顺序就是4 5 2 8 6 7 3 1。

由于树的结构是一层一层的，就像套娃一样，所以自然而然地，我们想到了用递归的形式来解决问题，我们称之为解法1。有递归的形式，自然就有非递归的形式，我们称之为解法2。

程序实现

解法1。

先序遍历。先序遍历是根节点，左子树，右子树的顺序，所以对于一个子树来说，按照这样的顺序打印即可。然后再对每一个子树递归这样的操作，即完成先序遍历。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

def preOrder(root):
    if root == None:
        return None
    print(root.val)
    preOrder(root.left)
    preOrder(root.right)

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

    preOrder(t1)

中序遍历原理差不多，就是打印的顺序变化一下，先打印左子树，然后根节点，然后右子树。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

def midOrder(root):
    if root == None:
        return None

    midOrder(root.left)
    print(root.val)
    midOrder(root.right)

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

    midOrder(t1)

后序遍历原理类似，先左子树，然后右子树，最后根节点。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

def latOrder(root):
    if root == None:
        return None

    latOrder(root.left)
    latOrder(root.right)
    print(root.val)

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

    latOrder(t1)

解法2。

由于有的面试官比较苛刻，会要求写出非递归的解法，因此写一下解法2。注意，解法2并非重点。

先序遍历。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

def preOrder(root):
    if root == None:
        return None

    stack = []
    tempNode = root
    while tempNode or stack:
        while tempNode:
            print(tempNode.val)
            stack.append(tempNode)
            tempNode = tempNode.left

        node = stack.pop()
        tempNode = node.right

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

    preOrder(t1)

中序遍历。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

def midOrder(root):
    if root == None:
        return None

    stack = []
    tempNode = root
    while tempNode or stack:
        while tempNode:
            stack.append(tempNode)
            tempNode = tempNode.left

        node = stack.pop()
        print(node.val)
        tempNode = node.right

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

    midOrder(t1)

后序遍历。

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

def latOrder(root):
    if root == None:
        return None

    stack = []
    tempNode = root
    while tempNode or stack:
        while tempNode:
            stack.append(tempNode)
            tempNode = tempNode.left

        node = stack[-1]
        tempNode = node.right
        if node.right == None:
            node = stack.pop()
            print(node.val)
            while stack and node == stack[-1].right:
                node = stack.pop()
                print(node.val)

if __name__ == '__main__':
    t1 = TreeNode(1)
    t2 = TreeNode(2)
    t3 = TreeNode(3)
    t4 = TreeNode(4)
    t5 = TreeNode(5)
    t6 = TreeNode(6)
    t7 = TreeNode(7)
    t8 = TreeNode(8)

    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    t3.right = t7
    t6.right = t8

    latOrder(t1)

‍

扫码关注