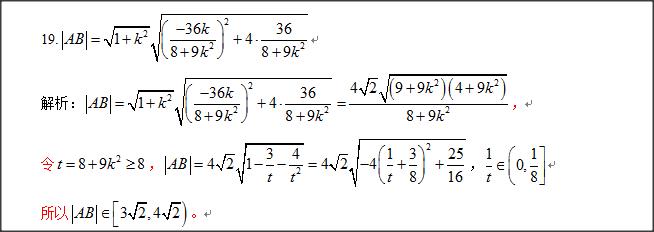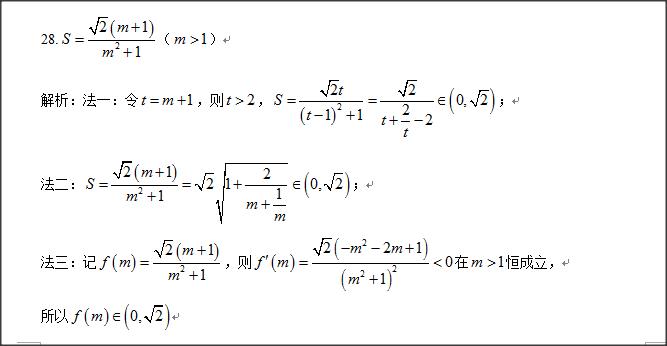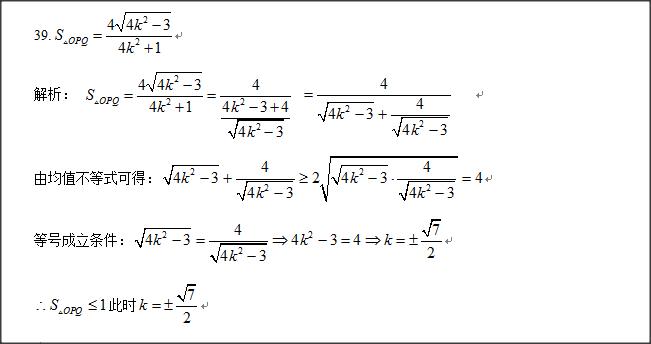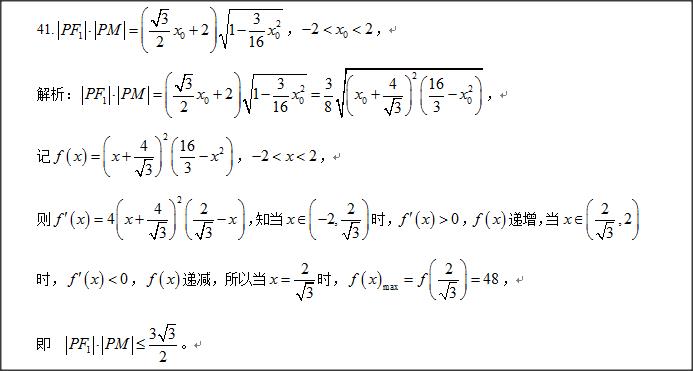解析几何中函数式的最值与值域问题专练

Posted 2021-04-09 高中数学课堂教学研究

诚邀您

点击左上角蓝字，进行关注

点击右下角在看，让更多人知道！

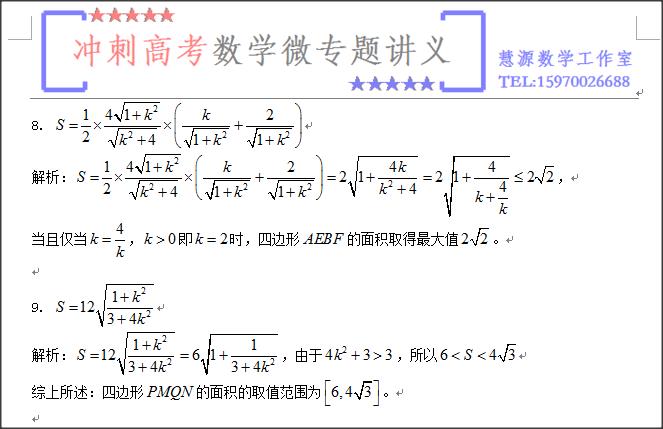
当我们处理解析几何有关元素的最值或者范围问题，经常会将该元素表示成一个含参数的解析式，进而转化为函数解析式来求其最值，而学生在遇到这个问题时，往往会受解析式的影响而无法下手，据此，本小编特意搜出40道有关的小题，随意打乱难易的顺序，共读者思考。

广告后有详细答案

广而告之

应广大教师朋友的回购要求，《十年自主招生真题分类汇编》已经进行第二次印刷，数量比第一次还少， 请有需要的老师注意进度，及时联系本小编（微信:B2L209）进行预订购买。

本书特色：

1. 方便携带：32开，410页。

2. 每个题目留有恰当的空白（不为了多几页而特意多留）

3. 题目之后，立马配上详细答案。

4. 题源来自：清华大学、北京大学、上海交大、浙大、中科大、复旦，2010-2014年的卓越联盟、华约、北约等名校真题回忆版（部分改动）。

5. 用途广泛：题目源于高考、低于竞赛，是你冲击985、211高校自招好帮手；是你参加竞赛的衔接助手；是一线老师校内培优、竞赛的好帮手！

6. 下面展示几何部分完整结构：

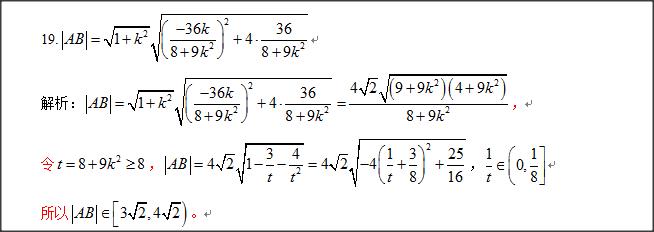
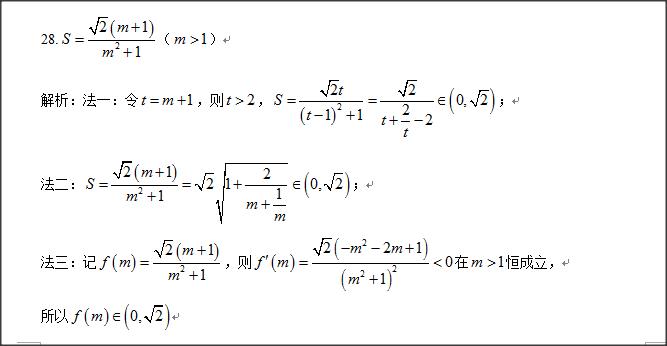
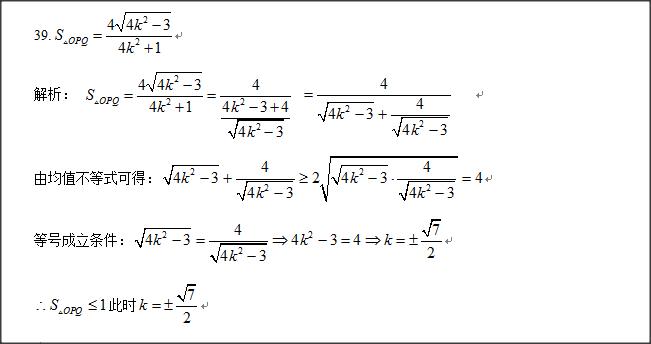
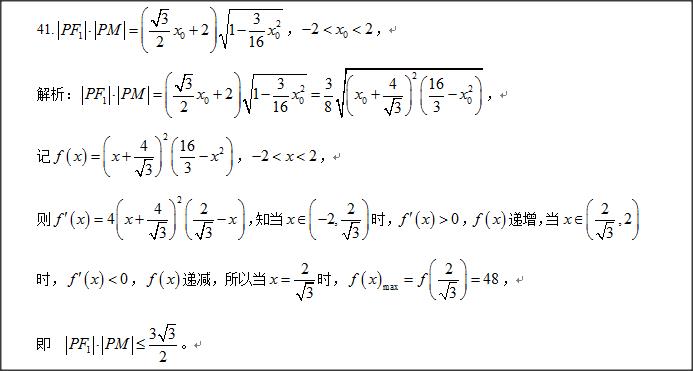
进行自我反思，学习总结，并且将反思、学习的结果与大家分享；倡导教师们多多进行教学探讨交流，提升个人专业能力，将探讨交流的结果与大家分享；倡导立足青蓝工程，以老推新，带动整体师资水平；倡导全中国教师放宽胸怀，做到资源共享！

广而告之2

应部分读者要求，应对强基计划，数学方面培训有啥建议，本人感觉，怎么变化，对数学的要求不会有多大的变化，对老师来说，平时如何通过课堂教学来提高学生应对教材内外的知识题型的处理能力是关键，切记：新形势下目标重点在高考，这样可以克服各种浮躁、好高骛远，再次，对课堂吸收快、能力强的学生进行加餐，提升他们的解决问题的能力，而不仅仅是解数学高考题的能力，跳出高考，站在过去自招的层面来看问题，以此拓宽视野、开发自己的素养空间，提升学科素养。所以，小编特意结合近几年自招真题回忆版、近几年各省市联赛预赛试题、高联决赛真题，对比高考的知识考点，精选部分真题，融合在一起，尽最大可能，通过自己的讲解，让学生悟出门道，又不会冲淡高考复习的主题。这里你会发现，没有平时的课堂基础，你入门不了，这种题，你入手不了，在这里，好高骛远，急功近利的孩子们再也没有优势了，所以还是那句话，作为老师，我们还是要重视基础，重视高考，平时课堂不能助力学生好高骛远，要讲知识本质，讲高考、自招、竞赛之间的联系及突破办法，作为学生，切记轻视高考题，盲目追求自招、竞赛题，因为万丈高楼平地起。

恳请大家多提宝贵意见，不足之处敬请批评指正！

在小编团队的快马加鞭下，在新增了几个主干力量的支持和努力下，本期讲义22讲正式和大家见面了，再次感谢所有支持和关注的朋友们，谢谢！

请读者们注意，我们团队特意给出三天（4月12-4月14日）的优惠活动已经截止了，（现在已经恢复原价60元一讲），谢谢惠顾！

仍然可商定赠送本公众号内重磅分享的内容的部分电子WORD版。