欧若纳算法解析聚类算法分析--FCM算法原理及特征
Posted 欧若纳Aurora
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了欧若纳算法解析聚类算法分析--FCM算法原理及特征相关的知识,希望对你有一定的参考价值。
FCM算法理解
FCM算法首先是由E. Ruspini提出来的,后来J. C. Dunn与J. C. Bezdek将E. Ruspini算法从硬聚类算法推广成模糊聚类算法。FCM算法是基于对目标函数的优化基础上的一种数据聚类方法。聚类结果是每一个数据点对聚类中心的隶属程度,该隶属程度用一个数值来表示。FCM算法是一种无监督的模糊聚类方法,在算法实现过程中不需要人为的干预。这种算法的不足之处:首先,算法中需要设定一些参数,若参数的初始化选取的不合适,可能影响聚类结果的正确性;其次,当数据样本集合较大并且特征数目较多时,算法的实时性不太好。
FCM算法工作原理


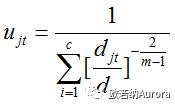

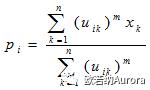
得到聚类中心值
FCM算法流程
算法流程:
(1) 标准化数据矩阵;
(2) 建立模糊相似矩阵,初始化隶属矩阵;
(3) 算法开始迭代,直到目标函数收敛到极小值;
(4) 根据迭代结果,由最后的隶属矩阵确定数据所属的类,显示最后的聚类结果。
FCM算法优缺点
优点:相比起前面的”硬聚类“,FCM方法会计算每个样本对所有类的隶属度,这给了我们一个参考该样本分类结果可靠性的计算方法,我们可以这样想,若某样本对某类的隶属度在所有类的隶属度中具有绝对优势,则该样本分到这个类是一个十分保险的做法,反之若该样本在所有类的隶属度相对平均,则我们需要其他辅助手段来进行分类。
缺点:该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。
往期回顾:
以上是关于欧若纳算法解析聚类算法分析--FCM算法原理及特征的主要内容,如果未能解决你的问题,请参考以下文章