聚类算法

Posted 2021-04-08 数学人生

聚类是一种无监督学习（无监督学习是指事先并不知道要寻找的内容，没有固定的目标变量）的算法，它将相似的一批对象划归到一个簇，簇里面的对象越相似，聚类的效果越好。聚类的目标是在保持簇数目不变的情况下提高簇的质量。给定一个 n 个对象的集合。把这 n 个对象划分到 K 个区域，每个对象只属于一个区域。所遵守的一般准则是：同一个簇的对象尽可能的相互接近或者相关，而不同簇的对象尽可能的区分开。最常见的一种聚类算法则是 K-均值 算法。

K-均值（K-Means）聚类算法

K 均值聚类算法是用来发现给定数据集的 K 个簇的一种无监督学习算法，簇的个数是由人工给定的，每个簇使用质心（Centroid）和相应的半径（Radius）来描述。需要量化的误差指标有误差平方和（sum of squared error）等。

K-均值算法是一种启发式的算法。它会渐近地提高聚类的质量，达到局部的最优解，但是就是因为这样，才容易陷入局部最优解，而没有达到全局最优解，所有有人提出了二分 K-均值算法。启发式的聚类算法很适合发现中小规模的簇，对于大数据集合，从计算量来说成本则会很高。K-均值算法也有着自己的不足之处，通过下面算法可以发现 K-均值算法对离群点特别敏感，离群点的存在会直接影响着 K-均值算法的效果。

K 均值算法的流程是这样的。首先，随机确定 K 个初始点作为质心。然后将数据集中的每个点分配到每一个簇中，具体来讲，为每一个数据点找距离其最近的质心，并将其分配给该质心所对应的簇。这一步完成之后，每个簇的质心更新为该簇所有点的平均值。

K-Means 的伪代码：

创建K个点作为初始的质心（经常是随机选择数据点中的K个点，而不是平面上随机的K个点）

当任意一个点的簇分配结果发生变化时：

    对数据集中每个数据点

        对每个质心，计算质心与数据点之间的距离

        将数据点分配到距离其最近的簇

    对每一个簇，计算簇中所有点的均值并将均值作为质心

注：K 均值算法在某些时候容易收敛到局部最小值。

使用一批二维数据集合，进行 4 均值聚类算法可以得到下图：’+’ 表示的是质心的位置，其余就是数据点的位置。

 

效果评估：

SSE 指的是 Sum of Squared Error（误差平方和）越小表示数据点越接近它们的质心，聚类的效果也就越好。质心使用 c[i] 表示，质心 c[i] 所包含的对象集合使用 C[i] 表示。如果用 p 表示 C[i] 中的某个对象，dist(p,c[i]) 表示的就是对象和质心 c[i] 的距离。那么误差平方和则定义为

 

二分 K 均值聚类（Bisecting K-Means）

为了解决 K 均值算法可能会收敛到局部最小值的情况，有人提出了二分 K 均值算法（bisecting K-means）。该算法首先将所有点作为一个簇，然后将该簇一分为二，之后选择其中的一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低 SSE 的值。上述基于SSE的划分过程不断重复，直到得到用户指定的簇的数目为止。

二分 K-Means 的伪代码如下：

将所有的点看成一个簇

当簇的数量小于K时

    对于每一个簇

        计算总误差

        在给定的簇上面进行2均值聚类

        计算将该簇一分为二之后的总误差（指的是这两个簇的误差与其他剩余集的误差之和）

    选择使得总误差最小的那个簇进行划分操作

另一种做法就是：每次进行下一步划分的时候，选择误差平方和最大的簇进行划分，直到簇的数目达到用户指定的数目为止。这样的启发式算法就使得整体的误差平方和尽可能的小，也就是簇的划分更加精确。

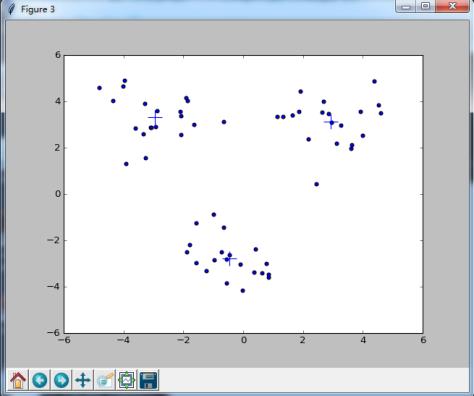
使用一批二维数据集合，进行 3 均值聚类算法可以得到下图：’+’ 表示的是质心的位置，其余就是数据点的位置。

 

相关文章推荐：

1.

2.

3.

欢迎大家关注公众账号数学人生