基础聚类算法：K-means算法

Posted 2021-04-08 智能算法

一、算法简介：

俗话说：“物以类聚，人以群分”，聚类算法不同于分类算法，对于一个 分类器 ，通常需要你告诉它“这个东西被分为某某类”这样一些例子，理想情况下，一个分类器 会从它得到的训练集中进行“学习”，从而具备对未知数据进行分类的能力，这种提供训练数据的过程通常叫做监督学习，而在聚类的时候，我们并不关心某一类是什么，我们需要实现的目标只是把相似的东西聚到一起，因此，一个聚类算法通常只需要知道如何计算相似度就可以开始工作了，因此聚类算法通常并不需要使用训练数据进行学习。以一句话来说明K-means算法的思路就是，在样本的某一维度特征上进行相似性度量（如常用度量距离：欧式距离,马式距离，汉明距离，余弦距离等），将相似度大小来估计样本所属类别。

作为机器学习，模式识别，数据挖掘等领域的常用算法，聚类分析是一种静态数据分析方法。从结构性来划分，聚类方法分为自上而下和自下而上两种方法，前者的算法是先把所有样本视为一类，然后不断从这个大类中分离出小类，直到不能再分为止；后者则相反，首先所有样本自成一类，然后不断两两合并，直到最终形成几个大类。

K-means聚类是一种自下而上的聚类方法，它的优点是思路简单、速度快；缺点是聚类结果与初始中心的选择有关系，且必须提供聚类的数目。K-means的第二个缺点是致命的，因为在有些时候，我们不知道样本集将要聚成多少个类别，这种时候K-means是不适合的，推荐使用hierarchical（层次聚类法） 或meanshift来聚类。第一个缺点可以通过多次聚类取最佳结果来解决。

二、具体实现：

在介绍 K-means 的具体步骤之前，让我们先来看看它对于需要进行聚类的数据的一个基本假设吧：对于每一个聚类簇（cluster），我们可以选出一个中心点 (center) ，使得该聚类簇中的所有的点到该中心点的距离小于到其他聚类簇的中心的距离。虽然实际情况中得到的数据并不能保证总是满足这样的约束，但这通常已经是我们所能达到的最好的结果，而那些误差通常是固有存在的或者问题本身的不可分性造成的。例如下图所示的两个高斯分布，从两个分布中随机地抽取一些数据点出来，混杂到一起，现在要让你将这些混杂在一起的数据点按照它们被生成的那个分布分开来：

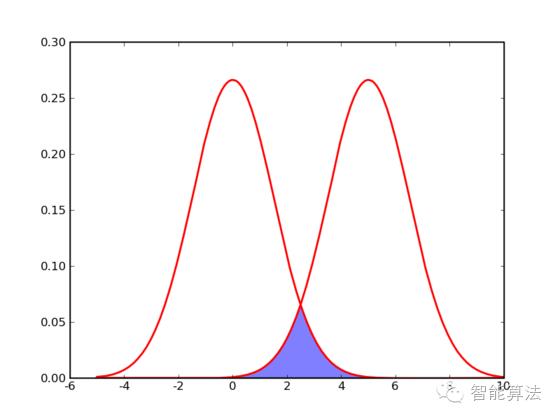
由于这两个分布本身有很大一部分重叠在一起了，例如，对于数据点 2.5 来说，它由两个分布产生的概率都是相等的，你所做的只能是一个猜测；稍微好一点的情况是 2 ，通常我们会将它归类为左边的那个分布，因为概率大一些，然而此时它由右边的分布生成的概率仍然是比较大的，我们仍然有不小的几率会猜错。而整个阴影部分是我们所能达到的最小的猜错的概率，这来自于问题本身的不可分性，无法避免。因此，我们将K-means 所依赖的这个假设看作是合理的。

基于这样一个假设，我们再来导出 K-means 所要优化的目标函数：设我们一共有 N 个数据点需要分为 K 个 cluster ，K-means 要做的就是最小化

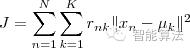
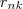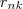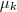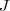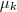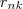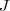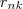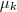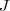这个函数，其中在数据点 n 被归类到 cluster k 的时候为 1 ，否则为 0 。直接寻找 和 来最小化 并不容易，不过我们可以采取迭代的办法：先固定，选择最优的 ，很容易看出，只要将数据点归类到离他最近的那个中心就能保证 最小。下一步则固定，再求最优的。将 对 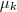求导并令导数等于零，很容易得到 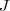最小的时候 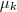应该满足：

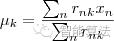
亦即 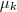 的值应当是所有 cluster k 中的数据点的平均值。由于每一次迭代都是取到 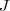的最小值，因此 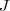只会不断地减小（或者不变），而不会增加，这保证了 K-means 最终会到达一个极小值。虽然 K-means 并不能保证总是能得到全局最优解，但是对于这样的问题，像 K-means 这种复杂度的算法，这样的结果已经是很不错的了。

下面我们来总结一下 K-means 算法的具体步骤：

1. 选定 K 个中心 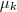的初值。这个过程通常是针对具体的问题有一些启发式的选取方法，或者大多数情况下采用随机选取的办法。因为前面说过 k-means 并不能保证全局最优，而是否能收敛到全局最优解其实和初值的选取有很大的关系，所以有时候我们会多次选取初值跑 k-means ，并取其中最好的一次结果。

2. 将每个数据点归类到离它最近的那个中心点所代表的 cluster 中。

3. 用公式 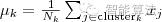 计算出每个 cluster 的新的中心点。

4. 重复第二步，一直到迭代了最大的步数或者前后的  的值相差小于一个阈值为止。

直观一点：如下图

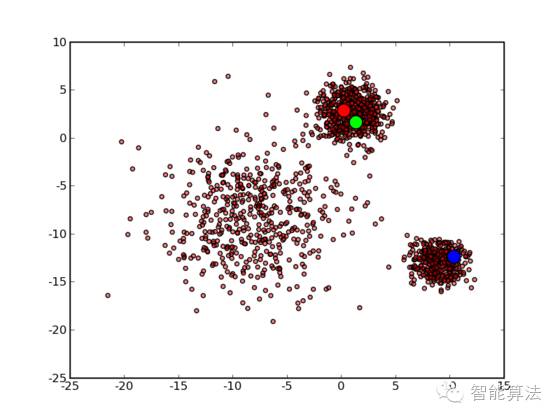
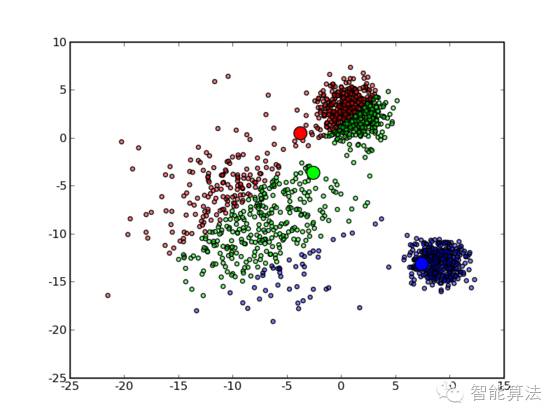
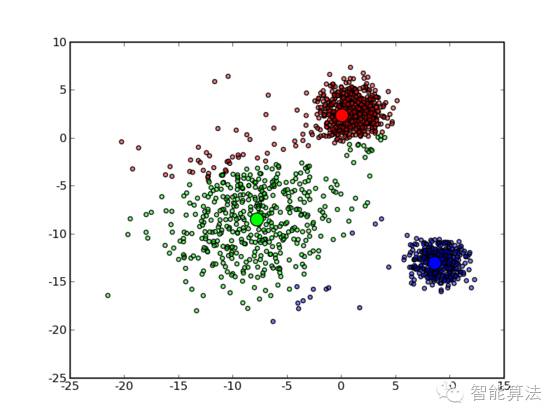
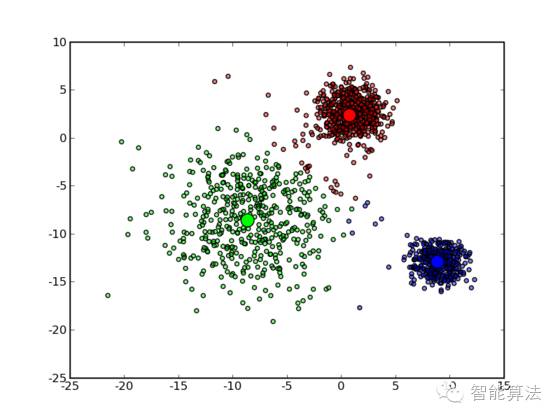
三、算法改进与讨论

对于算法来讲，计算效率、应用范围和如何改进缺陷，对于理解和使用的人一定是最为关心的三个要点：

首先，K-Means的计算复杂度为O(N*K)；经常以一些有限维度的特征向量的样本上，以不同的相似度量实现简单的聚类功能，如VRP问题中的客户群聚类，然后再进行车辆路径调度优化；还有用于图像分割当中，以像素点样本的像素特征进行聚类

原图

K为10

K为20

可以看出，并非K值越大，图像分割越好；

对于K-means的初始点不同聚类结果不同的缺陷改进，首先是可以用一些启发式的方式指定更好的初始质心。

选择适当的初始质心是基本kmeans算法的关键步骤。常见的方法是

1. 随机的选取初始质心，但是这样簇的质量常常很差。处理选取初始质心问题的一种常用技术是：多次运行，每次使用一组不同的随机初始质心，然后选取具有最小SSE（误差的平方和）的簇集。这种策略简单，但是效果可能不好，这取决于数据集和寻找的簇的个数。

2. 取一个样本，并使用层次聚类技术对它聚类。从层次聚类中提取K个簇，并用这些簇的质心作为初始质心。该方法通常很有效，但仅对下列情况有效：（1）样本相对较小，例如数百到数千（层次聚类开销较大）；（2）K相对于样本大小较小

3. 随机地选择第一个点，或取所有点的质心作为第一个点。然后，对于每个后继初始质心，选择离已经选取过的初始质心最远的点。使用这种方法，确保了选择的初始质心不仅是随机的，而且是散开的。但是，这种方法可能选中离群点。此外，求离当前初始质心集最远的点开销也非常大。为了克服这个问题，通常该方法用于点样本。由于离群点很少（多了就不是离群点了），它们多半不会在随机样本中出现。计算量也大幅减少。

4. Canopy Method算法:

Stage1、聚类最耗费计算的地方是计算对象相似性的时候，Canopy Method在第一阶段选择简单、计算代价较低的方法计算对象相似性，将相似的对象放在一个子集中，这个子集被叫做Canopy ，通过一系列计算得到若干Canopy，Canopy之间可以是重叠的，但不会存在某个对象不属于任何Canopy的情况，可以把这一阶段看做数据预处理；

Stage2、在各个Canopy 内使用传统的聚类方法(如K-means)，不属于同一Canopy 的对象之间不进行相似性计算。

从这个方法起码可以看出两点好处：首先，Canopy 不要太大且Canopy 之间重叠的不要太多的话会大大减少后续需要计算相似性的对象的个数；其次，类似于K-means这样的聚类方法是需要人为指出K的值的，通过Stage1得到的Canopy 个数完全可以作为这个K值，一定程度上减少了选择K的盲目性。

其他方法如贝叶斯信息准则方法（BIC）也可以应用。

这些改进也可以简称为K-means++算法，帮助算法本身在有限个样本点中选取合适的“种子质心”

而针对K-means的聚类簇个数初始指定问题，小编所熟知的就是通过一些交叉验证和指定一个合适的类簇指标，比如平均半径或直径，只要我们假设的类簇的数目等于或者高于真实的类簇的数目时，该指标上升会很缓慢，而一旦试图得到少于真实数目的类簇时，该指标会急剧上升。

类簇的直径是指类簇内任意两点之间的最大距离。

类簇的半径是指类簇内所有点到类簇中心距离的最大值。

废话不说，直接上图。下图是当K的取值从2到9时，聚类效果和类簇指标的效果图：

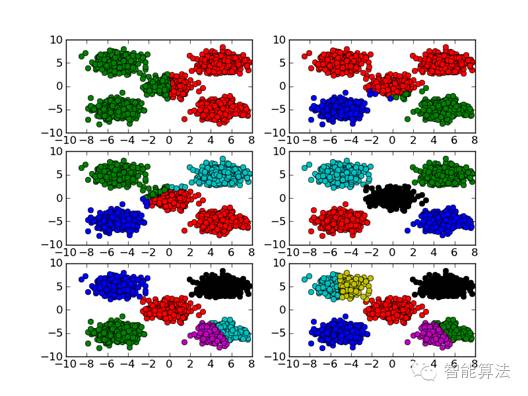
结论自然可知当K为5的时候，聚类更为合理！！

总结一下：算法除了要事先确定簇数K和对初始聚类中心敏感外，经常以局部最优结束，同时对“噪声”和孤立点敏感，并且该方法不适于发现非凸面形状的簇或大小差别很大的簇。

四、相关思考

从机器学习中统计概率的角度思考：

下面累述一下K-means与EM的关系，首先回到初始问题，我们目的是将样本分成k个类，其实说白了就是求每个样例x的隐含类别y，然后利用隐含类别将x归类。由于我们事先不知道类别y，那么我们首先可以对每个样例假定一个y吧，但是怎么知道假定的对不对呢？怎么评价假定的好不好呢？我们使用样本的极大似然估计来度量，这里是就是x和y的联合分布P(x,y)了。如果找到的y能够使P(x,y)最大，那么我们找到的y就是样例x的最佳类别了，x顺手就聚类了。但是我们第一次指定的y不一定会让P(x,y)最大，而且P(x,y)还依赖于其他未知参数，当然在给定y的情况下，我们可以调整其他参数让P(x,y)最大。但是调整完参数后，我们发现有更好的y可以指定，那么我们重新指定y，然后再计算P(x,y)最大时的参数，反复迭代直至没有更好的y可以指定。

     这个过程有几个难点，第一怎么假定y？是每个样例硬指派一个y还是不同的y有不同的概率，概率如何度量。第二如何估计P(x,y)，P(x,y)还可能依赖很多其他参数，如何调整里面的参数让P(x,y)最大。这些问题在以后的篇章里回答。

     这里只是指出EM的思想，E步就是估计隐含类别y的期望值，M步调整其他参数使得在给定类别y的情况下，极大似然估计P(x,y)能够达到极大值。然后在其他参数确定的情况下，重新估计y，周而复始，直至收敛。

     上面的阐述有点费解，对应于K-means来说就是我们一开始不知道每个样例x对应隐含变量也就是最佳类别c。最开始可以随便指定一个给它，然后为了让P(x,y)最大（这里是要让J最小），我们求出在给定c情况下，目标函数最小时的质心参数，然而此时发现，可以有更好的类别c（质心与样例x距离最小的类别）指定给样例x，那么c得到重新调整，上述过程就开始重复了，直到没有更好的c指定。这样从K-means里我们可以看出它其实就是EM的体现，E步是确定隐含类别变量c，M步更新其他参数（质心）来使J最小化。这里的隐含类别变量指定方法比较特殊，属于硬指定，从k个类别中硬选出一个给样例，而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程，有目标函数，也有参数变量，只是多了个隐含变量，确定其他参数估计隐含变量，再确定隐含变量估计其他参数，直至目标函数最优。

2007年natural上发表一篇关于基于仿射传播的聚类方法(Affinity-Propagation-Presentation)，在初始化时可以不用选取聚类簇的个数，有效的克服了K-means的致命缺陷，有兴趣的读者可以关注今日发布的下一篇文章！

五、参考资料

http://blog.csdn.net/qll125596718/article/details/8243404

http://www.cnblogs.com/easymind223/archive/2012/10/30/2747178.html

http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html

http://www.cnblogs.com/kemaswill/archive/2013/01/26/2877434.html

---

免责声明：本文系网络转载。版权归原作者所有。如涉及版权，请联系删除！