深入剖析Mean Shift聚类算法原理
Posted 机器学习算法那些事
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深入剖析Mean Shift聚类算法原理相关的知识，希望对你有一定的参考价值。
Mean Shift（均值漂移）是基于密度的非参数聚类算法，其算法思想是假设不同簇类的数据集符合不同的概率密度分布，找到任一样本点密度增大的最快方向（最快方向的含义就是Mean Shift），样本密度高的区域对应于该分布的最大值，这些样本点最终会在局部密度最大值收敛，且收敛到相同局部最大值的点被认为是同一簇类的成员。
Mean Shift在计算机视觉领域的应用非常广，如图像分割，聚类和视频跟踪，小编曾经用Mean Shift实现目标跟踪，效果还不错。本文详细的总结了Mean Shift算法原理。
目录
1.核密度估计
2.Mean Shift算法
3.图解Mean Shift算法
4.带宽对Mean Shift算法的影响
5.图像分割
6.聚类
7.Mean Shift算法优缺点
Mean Shift算法用核函数估计样本的密度，最常用的核函数是高斯核。它的工作原理是在数据集上的每一个样本点都设置一个核函数，然后对所有的核函数相加，得到数据集的核密度估计（kernel density estimation）。
假设我们有大小为n的d维数据集，核函数K的带宽为参数h。
数据集的核密度估计：
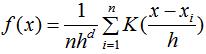
其中K(x)是径向对称函数（radially symmetric kernels），定义满足核函数条件的K(x)为：
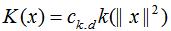
其中系数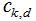
是归一化常数，使K(x)的积分等于1。
如下图，我们用高斯核估计一维数据集的密度，每个样本点都设置了以该样本点为中心的高斯分布，累加所有的高斯分布，得到该数据集的密度。
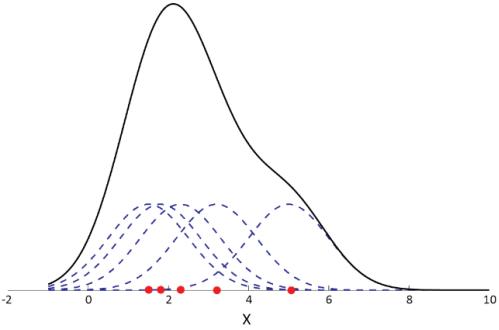
其中虚线表示每个样本点的高斯核，实线表示累加所有样本高斯核后的数据集密度。因此，我们通过高斯核来得到数据集的密度。
Mean Shift算法的基本目标是将样本点向局部密度增加的方向移动，我们常常所说的均值漂移向量就是指局部密度增加最快的方向。上节介绍了通过引入高斯核可以知道数据集的密度，梯度是函数增加最快的方向，因此，数据集密度的梯度方向就是密度增加最快的方向。
由上节可知，数据集密度：
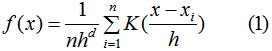
上式的梯度为：
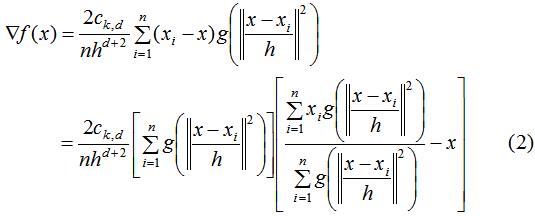
其中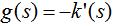
，上式的第一项为实数值，因此第二项的向量方向与梯度方向一致，第二项的表达式为：
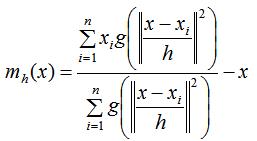
上式的含义就是本篇文章的主题：均值漂移。由上式推导可知：均值漂移向量所指的方向是密度增加最大的方向。
因此，Mean Shift算法流程为：
（1）计算每个样本的均值漂移向量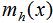
（2）对每个样本点以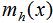进行平移，即：
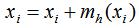
（3）重复（1）（2），直到样本点收敛，即：
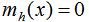
（4）收敛到相同点的样本被认为是同一簇类的成员
Mean Shift通过带宽来调节簇类的个数，本节用核概率密度的角度去理解带宽对Mean Shift算法的影响。
如下图是一维数据集的核概率密度，其中虚线表示每个样本的核函数，实线是每个样本的核函数进行叠加，表示数据集的概率密度。该数据集的概率密度只有一个局部最大值，因此，mean shift算法的簇类个数是1。
若我们设置带宽的值接近于0，那么数据集样本的核函数类似于冲激函数，如下图：
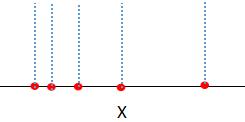
累加每个样本的核函数，得数据集的概率密度：
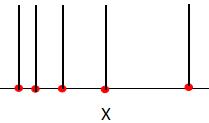
如上图，当带宽的值接近于0时，数据集的概率密度有5个局部最大值，mean shift算法的簇类个数是5。因此带宽决定了数据集的概率密度，进而影响了聚类结果。
mean shift通过对像素空间进行聚类，达到图像分割的目的。
我们对下图进行图像分割：
我们对上图的像素点映射为RGB三维空间：
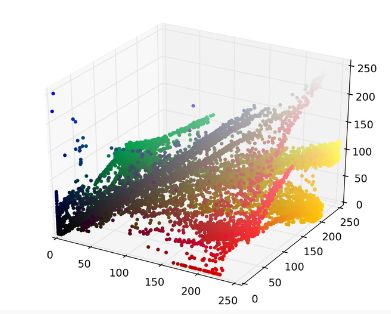
然后运行mean shift算法，使用带宽为25的高斯核，如下gif给出每个样本收敛到局部最大核密度的过程：
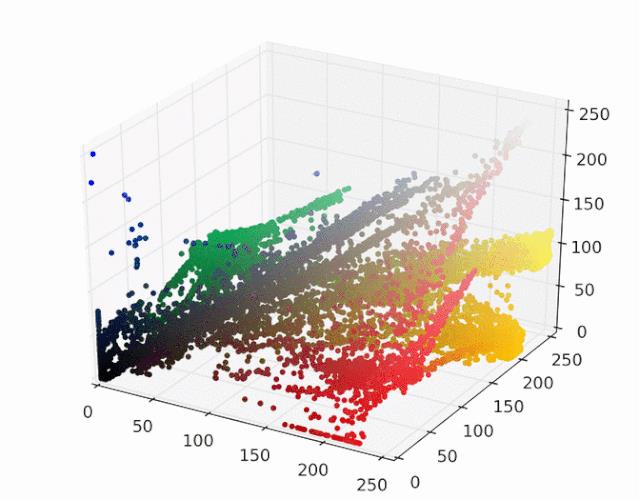
每个样本点最终会移动到核概率密度的峰值，移动到相同峰值的样本点属于同一种颜色，下图给出图像分割结果：
图像分割代码请参考github：
https://github.com/mattnedrich/MeanShift_py。
我们构建1000例4个簇类的样本数据：
#%% 产生样本数据
from sklearn.datasets import make_blobs
from itertools import cycle
from sklearn.cluster import MeanShift, estimate_bandwidth
centers = [[1, 1], [-.75, -1], [1, -1], [-3, 2]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
利用函数estimate_bandwidth估计核函数的带宽：
bandwidth = estimate_bandwidth(X, quantile=.1,n_samples=500)
运行mean shift算法，并可视化聚类结果：
优点：
不需要设置簇类的个数；
可以处理任意形状的簇类；
算法只需设置带宽这一个参数，带宽影响数据集的核密度估计
算法结果稳定，不需要进行类似K均值的样本初始化
缺点：
聚类结果取决于带宽的设置，带宽设置的太小，收敛太慢，簇类个数过多；带宽设置的太大，一些簇类可能会丢失。
对于较大的特征空间，计算量非常大。
参考：
https://spin.atomicobject.com/2015/05/26/mean-shift-clustering/
http://efavdb.com/mean-shift/
推荐阅读
以上是关于深入剖析Mean Shift聚类算法原理的主要内容，如果未能解决你的问题，请参考以下文章
基于mean shift算法的物体跟踪(python+opencv代码）