决策树(DecisionTree)和随机森林(Random Forests)
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了决策树(DecisionTree)和随机森林(Random Forests)相关的知识,希望对你有一定的参考价值。
参考技术A 令N为训练样例的个数,则单棵决策树的输入样例的个数为N个从训练集中有放回的 随机 抽取N个训练样例。令训练样例的输入特征的个数为M,我们在每颗决策树的每个节点上进行分裂时,从M个输入特征里 随机 选择m个输入特征,且m远远小于M。然后从这m个输入特征里选择一个最好的进行分裂。 m在构建决策树的过程中不会改变 。
构建决策树的算法主要有以下三种,且根据决策树的输出结果,决策树可以分为 分类树 和 回归树 ,分类树输出的结果为具体的类别,而回归树输出的结果为一个确定的数值。其中 ID3 和 C4.5 是分类树, CART 是分类回归树,且 在ID3 和 C4.5 中,特征(属性)只能选一次,而 CART 没有这样的要求 :
a. ID3 在决策树生成过程中,以 信息增益 为特征选择的准则。
b. C4.5 在决策树生成过程中,以 信息增益比 为特征选择的准则。
c. CART 对回归树用 平方误差最小化准则 ,对分类树用 基尼指数 (Gini index) 最小化准则 ,进行特征选择,生成二叉树。
例:
图1左中的信息增益InfoGain1 及信息增益比 InfoRatio1为:
同理,图1右的信息增益 InfoGain2 及 InfoRatio2 分别为:
由于 InfoGain1 > InfoGain2, 所以由ID3算法选择第一种方法;
由于InfoRatio1 > InfoRatio2 ,所以根据C4.5算法选择第一种方法
当节点的数据量小于一个指定的数量时,不继续分裂。两个原因:一是数据量较少时,再做分裂容易强化噪声数据的作用;二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
由上述可知,熵和基尼值的大小表示数据的复杂程度,当熵或者基尼值过小时,表示数据的纯度比较大,如果熵或者基尼值小于一定程度数,节点停止分裂。
节点的深度可以理解为节点与决策树跟节点的距离,如根节点的子节点的深度为1,因为这些节点与跟节点的距离为1,子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度,当深度到达指定的上限大小时,停止分裂。
按照1生成t个决策树之后,对于每个新的测试样例,综合多个决策树的分类结果来作为随机森林的分类结果。
(1)目标特征为 数字类型 :取t个决策树的 平均值 作为分类结果。
(2)目标特征为 类别类型 : 少数服从多数 ,取单棵树分类结果最多的那个类别作为整个随机森林的分类结果。
在随机森林中,无需交叉验证来评价其分类的准确性,随机森林自带 OOB(out-of-bag)错误估计 :
OOB:在构造单棵决策树时我们只是随机有放回的抽取了N个样例,所以可以用没有抽取到的样例来测试这棵决策树的分类准确性,这些样例大概占总样例数目的三分之一。
所以对于每个样例j,都有大约三分之一的决策树(记为SetT(j))在构造时没用到该样例,我们就用这些决策树来对这个样例进行分类。我们对于所有的训练样例 j,用SetT(j)中的树组成的森林对其分类,然后看其分类结果和实际的类别是否相等,不相等的样例所占的比例就是OOB错误估计。OOB错误估计被证明是无偏的。
备战数学建模43-决策树&随机森林&Logistic模型(攻坚站7)
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。随机森林 (Random forest)[5] 是由美国科学家 Leo Breiman 将其在 1996 年提出的
Bagging 集成学习理论 与 Ho 在 1998 年提出的随机子空间方法相结合,于 2001 年发
表的一种机器学习算法。logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率,等等。例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌,即“是”或“否”,为两分类变量,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。通过logistic回归分析,就可以大致了解到底哪些因素是胃癌的危险因素。
目录
一、决策树
1.1、决策树算法概述
决策树就是从根节点到叶子节点一步步做决策的模型,最终所有的决策都会落在叶子节点,这样该模型既可以做分类,也可以做回归。决策树有严格的先后顺序,每次决策类型的顺序不能发生改变,在前面的节点的重要性要比在后面的节点的重要性要高,
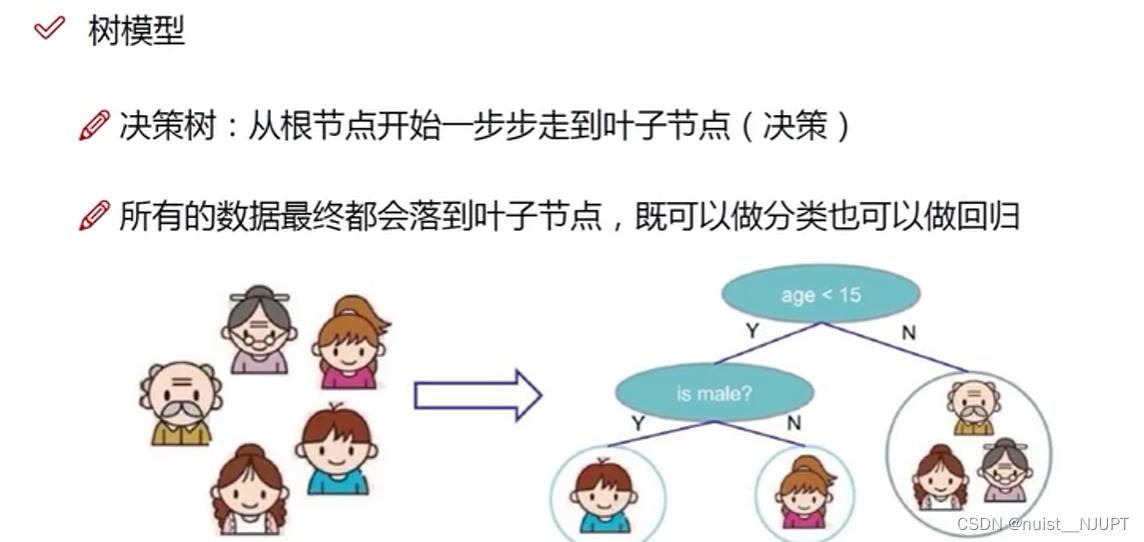
决策树的组成如下:从根节点到叶子节点,最终的决策在叶子节点。
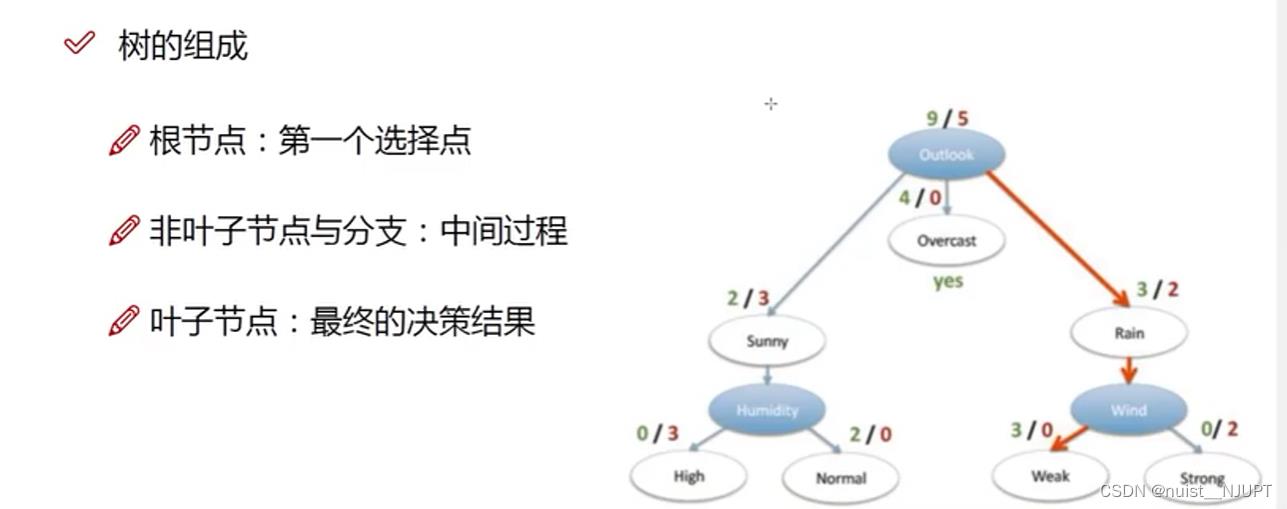
决策树的训练:根据数据构造决策树,测试:有了决策树后从上到下走一遍。

1.2、熵值的作用
我们在构造决策树的时候需要根据特征的重要性进行切分,即根据区分效果划分节点,那么如何衡量每个特征的重要性呢?一般使用熵值去衡量。

我们使用熵值去衡量决策树特征的好坏,熵值越小,说明越确定,即相对稳定,

选择信息熵小的,使得按该特征分类后的该类的不确定性程度减小的多。

1.3、决策树构造实例
有一份数据包含14天打球情况,根据已有的数据,根据4种环境变化特征构建一个决策树,判断未来某一天的环境下是否去打球。

现在根据数据基于下面四个特征进行决策树划分,我们首先需要找到根节点,四个特征谁当根节点最好呢?当然是信息熵越小的越好,即信息增益越大越好,也就是max(原始信息熵-以该特征为节点的信息熵).
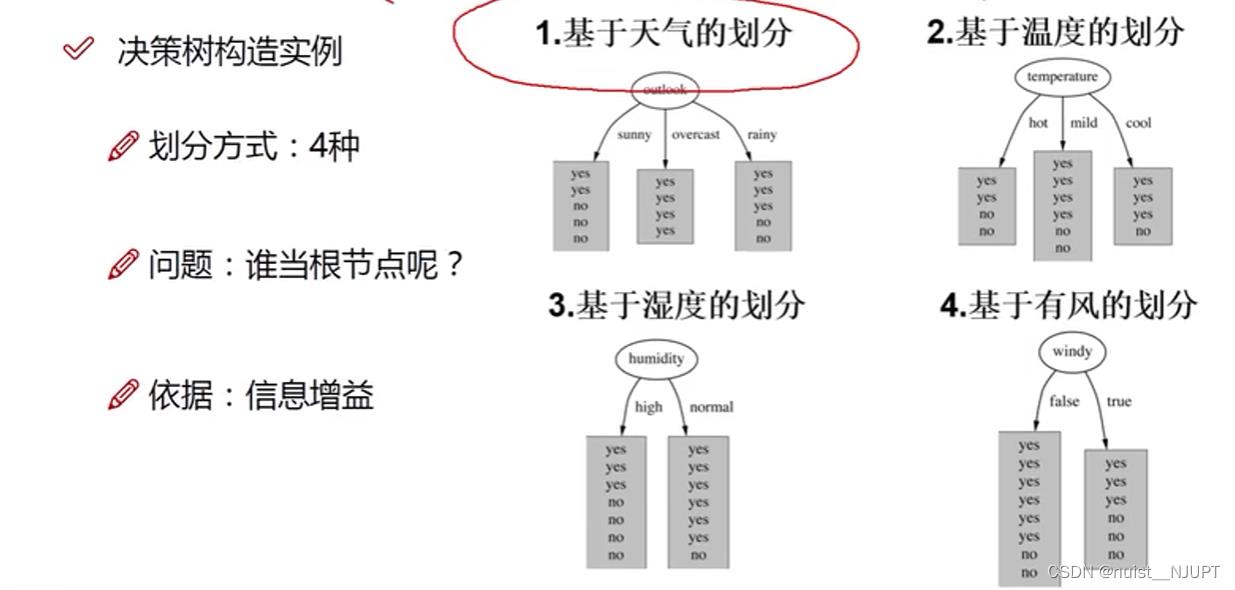
在计算各个特征的信息熵之前,我们需要对原始数据的信息熵进行计算,然后才能计算信息增益,基于play进行计算,14天有9天打球,5天不打球,代入公式得到信息熵为0.94.那么在此基础上,要分别计算基于其余特征的划分情况下的信息熵。

我们计算得到基于天气的熵值为0.693,则信息增益是0.247.然后同样的方法计算出基于温度的信息增益,基于湿度的信息增益,基于是否有风的信息增益,最后将信息增益最后的特征作为根节点,然后按照同样的方式划分下层节点。

1.4、信息增益率与gini系数
我们常用的决策树算法是ID3,C4.5,CART,如下所示:基尼系数的值越小,则效果越好。

1.5、剪枝的方法
为了防止数据出现过拟合的情况,即在训练集表现很好,在测试集表现的并不好。则需要进行剪枝,主要有预剪枝和后剪枝,预剪枝在建立决策树的过程中剪枝,后剪枝是建立完树后剪枝。

对于预剪枝的策略,一般通过限制深度,叶子节点个数,信息增益量等方法去剪枝,如果是后剪枝方法,需要根据公式进行衡量是否进行剪枝。
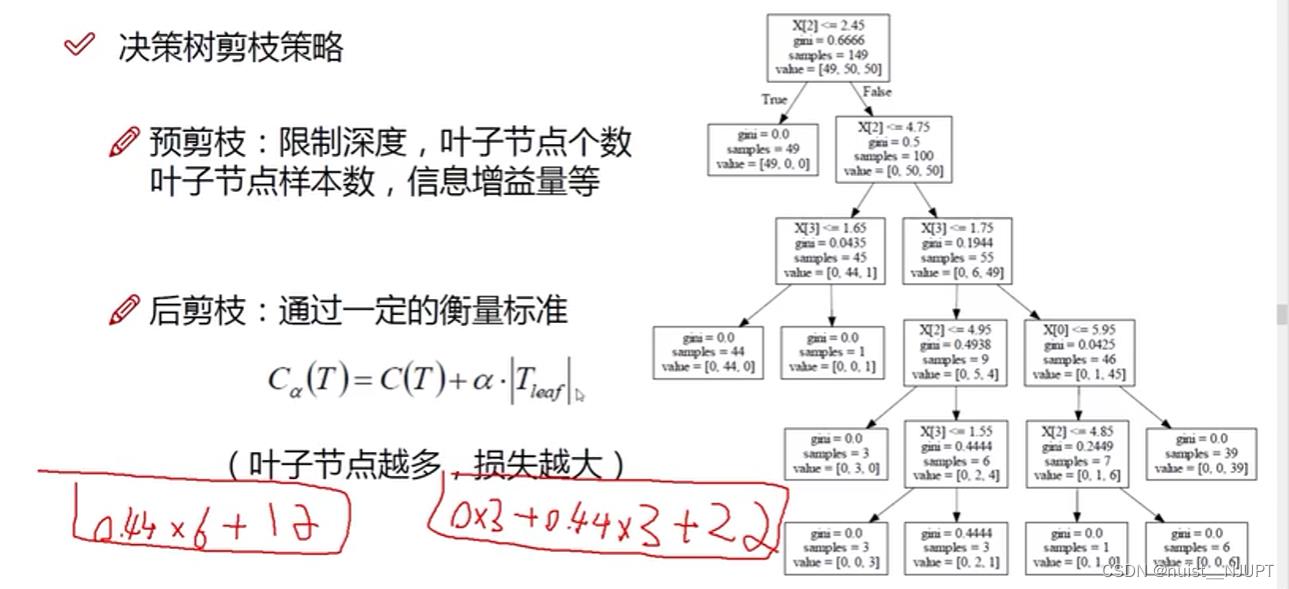
1.6、决策树实验案例及分析
构建决策树的方法主要有三种:ID3,C4.5,CART。
首先我们使用14组环境数据作为数据集,前12组用来训练构造树,后2组用来预测。
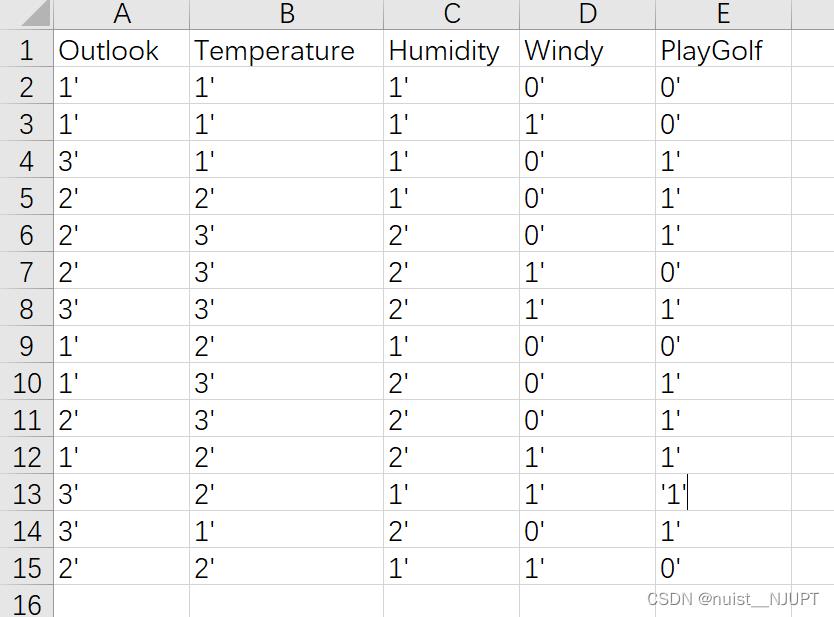
我们可以先看一下效果,构建的决策树和最后两组的预测结果如下:


我们再换用如下西瓜数据集进行训练和测试,构建的决策树和测试结果如下:

 具体的matlab代码如下:
具体的matlab代码如下:
主函数代码如下:
clear
clc
load('watermelon.mat')
%load('datas.mat')
%watermelon = datas ;
size_data = size(watermelon); %watermelon2为导入工作台的数据
%分为训练集和测试集
x_train = watermelon(1:size_data(1)-2,:) %这里加上了属性标签行
x_test = watermelon(size_data(1)-1:end,1:size_data(2)-1); %选择最后两个当测试集
%训练
size_data = size(x_train);
dataset = x_train(2:size_data(1),:); %纯数据集
labels = x_train(1,1:size_data(2)-1); %属性标签
%生成决策树
mytree = ID3(dataset,labels);
[nodeids,nodevalue,branchvalue] = print_tree(mytree);
tree_plot(nodeids,nodevalue,branchvalue);
predict(x_test,mytree,x_train(1,1:end-1)) 构建决策树代码如下:
function myTree = ID3(dataset,labels)
% ID3算法构建决策树
% 输入参数:
% dataset:数据集
% labels:属性标签
% 输出参数:
% tree:构建的决策树
size_data = size(dataset);
classList = dataset(:,size_data(2)); %得到标签
%全为同一类,熵为0
if length(unique(classList))==1
myTree = char(classList(1));
return
end
%去除完全相同的属性,避免产生没有分类结果的节点
% choose=ones(1,size_data(2));
% for i=1:(size_data(2)-1)
% featValues = dataset(:,i);
% uniqueVals = unique(featValues);
% if(length(uniqueVals)<=1)
% choose(i)=0;
% end
% end
% labels=labels((choose(1:size_data(2)-1))==1);
% dataset=dataset(:,choose==1);
size_data = size(dataset);
classList = dataset(:,size_data(2));
%%属性集为空,用找最多数
if size_data(2) == 1
temp=tabulate(classList);
value=temp(:,1); %属性值
count=cell2mat(temp(:,2)); %不同属性值的各自数量
index=find(max(count)==count);
choose=index(randi(length(index)));
myTree = char(value(choose));
return
end
%bestFeature = chooseFeature(dataset); %找到信息增益最大的特征
bestFeature = chooseFeatureGini(dataset); %找到信息增益最大的特征
bestFeatureLabel = char(labels(bestFeature)); %得到信息增益最大的特征的名字,即为接下来要删除的特征
myTree = containers.Map;
leaf = containers.Map;
featValues = dataset(:,bestFeature);
uniqueVals = unique(featValues);
labels=[labels(1:bestFeature-1) labels(bestFeature+1:length(labels))]; %删除该特征
%形成递归,一个特征的按每个类别再往下分
for i=1:length(uniqueVals)
subLabels = labels(:)';
value = char(uniqueVals(i));
subdata = splitDataset(dataset,bestFeature,value); %取出该特征值为value的所有样本,并去除该属性
leaf(value) = ID3(subdata,subLabels);
myTree(char(bestFeatureLabel)) = leaf;
end
end构建决策树过程中根据基尼指数选择特征的代码:
function bestFeature=chooseFeatureGini(dataset,~)
% 选择基尼指数最小的属性特征
%数据预处理
[N,M]=size(dataset); %样本数量N
M=M-1; %特征个数M
y=strcmp(dataset(:,M+1),dataset(1,M+1)); %标签y(以第一个标签为1)
x=dataset(:,1:M); %数据x
Gini_index = zeros(1,M); %创建一个数组,用于储存每个特征的信息增益
%bestFeature; %最大基尼系数的特征
%计算基尼指数
for i=1:M
% 计算第i种属性的基尼指数
temp=tabulate(x(:,i));
value=temp(:,1); %属性值
count=cell2mat(temp(:,2)); %不同属性值的各自数量
Kind_Num=length(value); %取值数目
Gini=zeros(Kind_Num,1);
% i属性下 j取值的基尼指数
for j=1:Kind_Num
% 在第j种取值下正例的数目
Gini(j)= getGini( y(strcmp(x(:,i),value(j))) );
end
Gini_index(i)=count'/N*Gini;
end
%随机挑选一个最小值
min_GiniIndex=find(Gini_index==min(Gini_index));
choose=randi(length(min_GiniIndex));
bestFeature=min_GiniIndex(choose);
end计算基尼指数的代码如下:
function Gini = getGini(y)
% 计算基尼系数
% y对应的标签,为1或0,对应正例与反例
%%%%%%===============================================================================
N=length(y); %标签长度
P_T=sum(y)/N; %正例概率
P_F=1-P_T; %正例概率
Gini=1-P_T*P_T-P_F*P_F; %基尼系数
%%%%%%===============================================================================
end构造决策树的过程中,划分数据集的方法:
function subDataset = splitDataset(dataset,axis,value)
%划分数据集,axis为某特征列, 取出该特征值为value的所有样本,并去除该属性
subDataset = ;
data_size = size(dataset);
%取 该特征列 该属性 对应的数据集
for i=1:data_size(1)
data = dataset(i,:);
if strcmp(cellstr(data(axis)),cellstr(value))
subDataset = [subDataset;[data(1:axis-1) data(axis+1:length(data))]]; %取 该特征列 该属性 对应的数据集
end
end
end遍历决策树的方法:
function [nodeids_,nodevalue_,branchvalue_] = print_tree(tree)
% 层序遍历决策树,返回nodeids(节点关系),nodevalue(节点信息),branchvalue(枝干信息)
nodeids(1) = 0;
nodeid = 0;
nodevalue=;
branchvalue=;
queue = tree ; %形成队列,一个一个进去
while ~isempty(queue)
node = queue1;
queue(1) = []; %在队列中除去该节点
if strcmp(cellstr(class(node)),'containers.Map') == 0 %叶节点的话(即走到底了)
nodeid = nodeid+1;
nodevalue = [nodevalue,node];
elseif length(node.keys)==1 %节点的话
nodevalue = [nodevalue,node.keys]; %储存该节点名
node_info = node(char(node.keys)); %储存该节点下的属性对应的map
nodeid = nodeid+1;
branchvalue = [branchvalue,node_info.keys]; %每个节点下的属性
for i=1:length(node_info.keys)
nodeids = [nodeids,nodeid];
end
end
if strcmp(cellstr(class(node)),'containers.Map')
keys = node.keys();
for i = 1:length(keys)
key = keysi;
queue=[queue,node(key)]; %队列变成该节点下面的节点
end
end
nodeids_=nodeids;
nodevalue_=nodevalue;
branchvalue_ = branchvalue;
end绘制决策树的方法:
function tree_plot(p,nodevalue,branchvalue)
% 参考treeplot
[x,y,h] = treelayout(p); %x:横坐标,y:纵坐标;h:树的深度
f = find(p~=0); %非0节点
pp = p(f); %非0值
X = [x(f); x(pp); NaN(size(f))];
Y = [y(f); y(pp); NaN(size(f))];
X = X(:);
Y = Y(:);
n = length(p);
if n<500
hold on;
plot(x,y,'ro',X,Y,'r-')
nodesize = length(x);
for i=1:nodesize
text(x(i)+0.01,y(i),nodevalue1,i);
end
for i=2:nodesize
j = 3*i-5;
text((X(j)+X(j+1))/2-length(char(branchvalue1,i-1))/200,(Y(j)+Y(j+1))/2,branchvalue1,i-1)
end
hold off
else
plot(X,Y,'r-');
end
xlabel(['height = ' int2str(h)]);
axis([0 1 0 1]);
end测试集进行预测的方法:
function y_test=predict(x_test,mytree,feature_list)
%测试
y_test = ;
row = size(x_test);
for j= 1:row(1)
queue = mytree; %形成队列,一个一个进去
feature_name = 0;
feature = 0;
while ~isempty(queue)
node = queue1;
queue(1) = []; %在队列中除去该节点
tag = 2;
if strcmp(cellstr(class(node)),'containers.Map') == 0%叶节点的话(即走到底了)
y_testj = node; %走到底就是我们需要的标签
continue
elseif length(node.keys)==1 %节点的话
feature_name = char(node.keys); %得到mytree节点的名字
id = ismember(feature_list,feature_name); %mytree该特征所在的坐标
x = x_test(j,:);
feature = x(id); %得到测试数据的特征属性
tag = 1;
end
%tag==2 即要走入下个节点
if tag==2
if strcmp(cellstr(class(node)),'containers.Map')
hasKeys=0;
keys = node.keys();
for i = 1:length(keys)
key = keysi;
c = char(feature);
if strcmp(key,c)
queue=[queue,node(key)]; %队列变成该节点下面的节点
hasKeys=1;
end
end
if(~hasKeys)
key = keysrandi(length(keys));
queue=[queue,node(key)]; %队列变成该节点下面的节点
end
end
end
%tag==1 即要选则符合测试数据的特征属性,这样就不用历遍整个mytree
if tag==1
if strcmp(cellstr(class(node)),'containers.Map')
keys = node.keys();
for i = 1:length(keys)
key = keysi;
queue=[queue,node(key)]; %队列变成该节点下面的节点
end
end
end
end
if length(y_test)<j
test=1;
end
end
end
二、随机森林
2.1、随机森林的算法原理
我们首先看卡集成算法,也可以叫集成学习,目的是让机器的学习效果更好,常见的又bagging,boosting和stacking,其中bagging是训练多个取平均值,boosting是训练多个组合加权,stacking是聚合多个分类,就是融合多个算法。

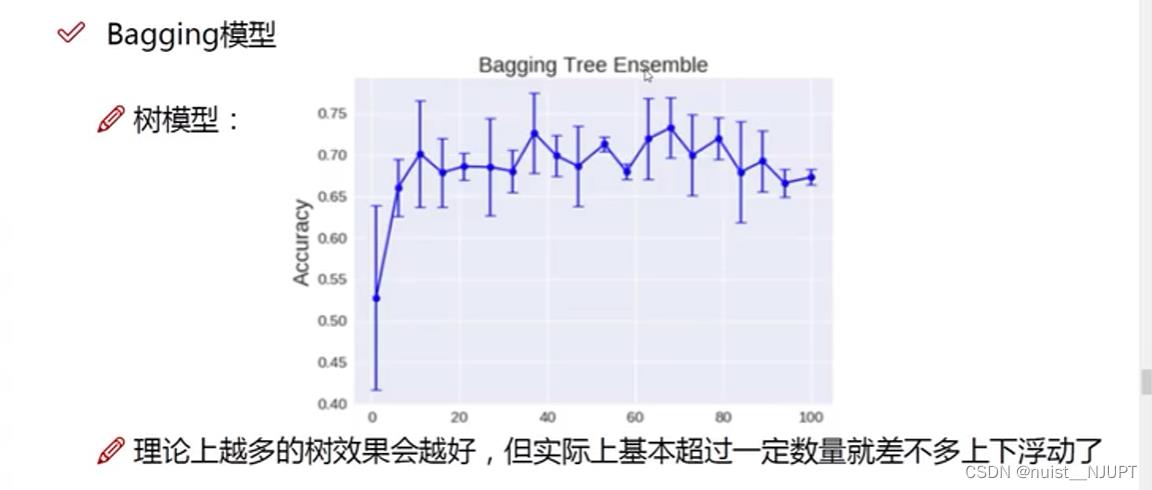
我们看一下Bagging模型,典型的Bagging模型就是随机森林,并行的训练一堆分类器,数据随机采样,特征选择随机,建立多个决策树,即多个分类器,将多个分类器放到一起就组成了森林。

通过2重随机性,就是随机采样,随机获取特征,使得构造的决策树具有多样性,最后的平均才能取得更好的效果,更具有说服力。

2.2、随机森林的优势与特征重要指标
随机森林的可解释性很强,神经网络虽然也可以用来预测和分类,但是神经网络的隐含层不具有可解释性,我们只知道输入和输出,具体内部怎么做的,细节无从得知。随机森林方便进行可视化展示,可以自动做特征筛选,并行速度较快。
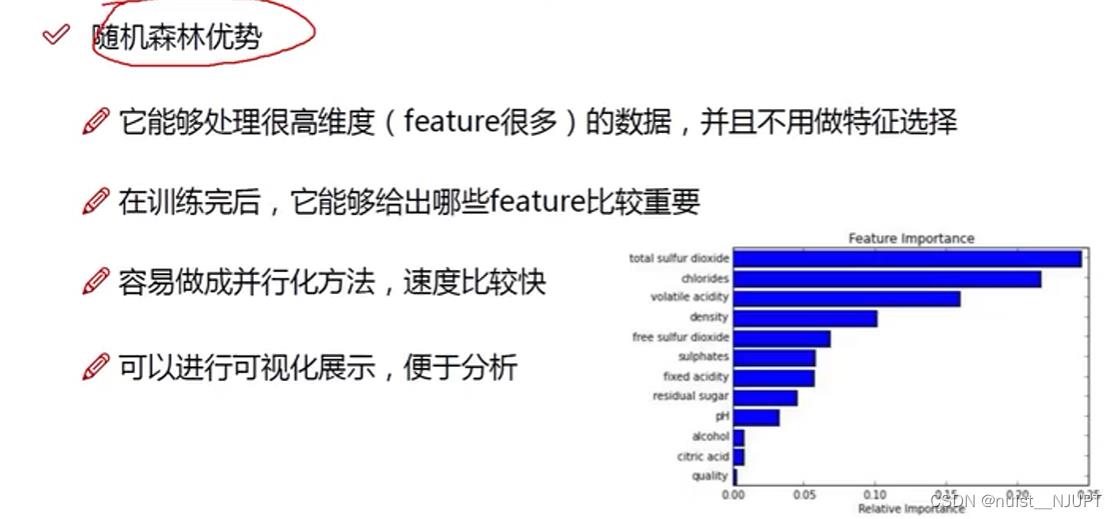
对于随机森林中决策树的个数应该为多少个呢,我们看这个图,可以发现当决策树达到一定的数量,准确率就趋于稳定了。
2.3、随机森林的分类过程
训练随机森林的过程就是训练各个决策树的过程,由于各个决策树的训练是相互独立的,因此随机森林的训练可以通过并行处理来实现,这将大大提高生成模型的效率。当输入待分类样本时,随机森林输出的分类结果由每个决策树的分类结果简单投票决定,随机森林的思想是:随机选取样本构造决策树,随机选取特征进行分裂。

随机森林的最终分类结果是取众数的方式,或者理解为取平均的方式。

分类过程可以近似表示为如下:

2.4、随机森林的实验案例及分析
我们先看一下我用的数据集,我用的还是上面决策树案例用到的根据环境状况判断是否打球的数据集合,14组数据。
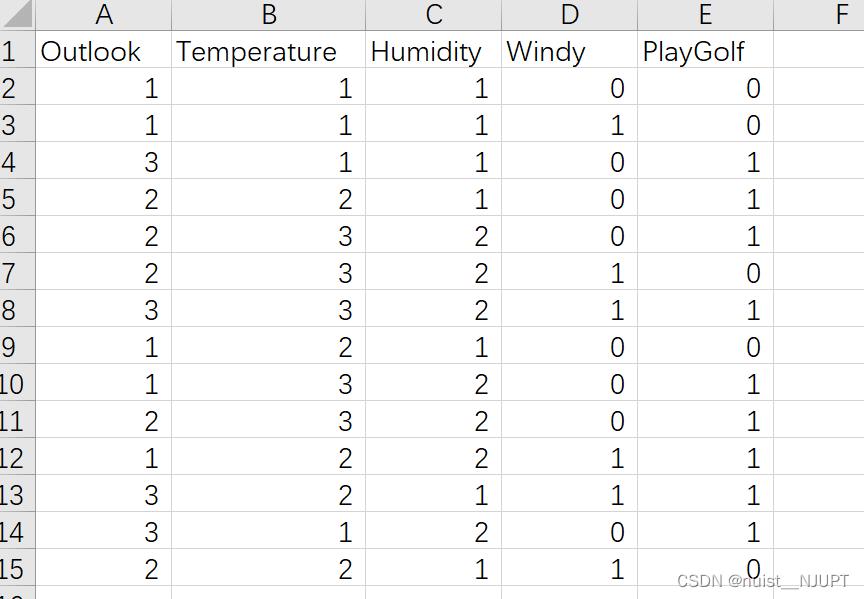
第一步:确定决策树的个数和决策树叶子节点数量,其中,RFOptimizationNum是为了多次循环,防止最优结果受到随机干扰;大家如果不需要,可以将这句话删除。
这里决策树的个数设置1~500,在这个范围内寻找最合适的决策树个数。
RFLeaf定义初始的叶子节点个数,我这里设置了从5到500,也就是从5到500这个范围内找到最优叶子节点个数。
Input与Output分别是我的输入(自变量)与输出(因变量),大家自己设置即可。
clc
clear
load('data1.mat')
Input = data1(2:end,1:end-1)
Output = data1(2:end,end)
%% 确定叶子节点和决策树的数量
for RFOptimizationNum=1:5
RFLeaf=[5,10,20,50,100,200,500];
col='rgbcmyk';
figure('Name','RF Leaves and Trees');
for i=1:length(RFLeaf)
RFModel=TreeBagger(500,Input,Output,'Method','R','OOBPrediction','On','MinLeafSize',RFLeaf(i));
plot(oobError(RFModel),col(i));
hold on
end
xlabel('Number of Grown Trees');
ylabel('Mean Squared Error') ;
LeafTreelgd=legend('5' '10' '20' '50' '100' '200' '500','Location','NorthEast');
title(LeafTreelgd,'Number of Leaves');
hold off;
disp(RFOptimizationNum);
end
我们从图中分析可以发现这个数据集选5个叶子节点,决策树的数量选取200左右就可以。其实由于该数据集数量较少,总的来说,决策树的叶子数量选取产生的误差相差不大。

选择好决策树的个数和叶子节点数,后面就可以对数据集进行划分,然后建立随机森林进行分类预测,可以计算出预测误差和每个特征的重要性排名,重要性越大,说明该特征对分类的作用越好。
clc
clear
load('data1.mat')
Input = data1(2:end,1:end-1) ;
Output = data1(2:end,end) ;
% %% 确定叶子节点和决策树的数量
% for RFOptimizationNum=1:5
% RFLeaf=[5,10,20,50,100,200,500];
% col='rgbcmyk';
% figure('Name','RF Leaves and Trees');
% for i=1:length(RFLeaf)
% RFModel=TreeBagger(500,Input,Output,'Method','R','OOBPrediction','On','MinLeafSize',RFLeaf(i));
% plot(oobError(RFModel),col(i));
% hold on
% end
% xlabel('Number of Grown Trees');
% ylabel('Mean Squared Error') ;
% LeafTreelgd=legend('5' '10' '20' '50' '100' '200' '500','Location','NorthEast');
% title(LeafTreelgd,'Number of Leaves');
% hold off;
% disp(RFOptimizationNum);
% end
%% 循环准备
RFScheduleBar=waitbar(0,'Random Forest is Solving...');
RFRMSEMatrix=[];
RFrAllMatrix=[];
RFRunNumSet=5000;
for RFCycleRun=1:RFRunNumSet
%% 训练集和测试集的划分
RandomNumber=(randperm(length(Output),floor(length(Output)*0.2)))';
TrainYield=Output;
TestYield=zeros(length(RandomNumber),1);
TrainVARI=Input;
TestVARI=zeros(length(RandomNumber),size(TrainVARI,2));
for i=1:length(RandomNumber)
m=RandomNumber(i,1);
TestYield(i,1)=TrainYield(m,1);
TestVARI(i,:)=TrainVARI(m,:);
TrainYield(m,1)=0;
TrainVARI(m,:)=0;
end
TrainYield(all(TrainYield==-2,2),:)=[];
TrainVARI(all(TrainVARI==-2,2),:)=[];
end
%% 随机森林
nTree=200;
nLeaf=5;
RFModel=TreeBagger(nTree,TrainVARI,TrainYield,...
'Method','regression','OOBPredictorImportance','on', 'MinLeafSize',nLeaf);
[RFPredictYield,RFPredictConfidenceInterval]=predict(RFModel,TestVARI);
disp('预测结果:') ;
disp(RFPredictYield) ;
%% 计算误差
RFRMSE=sqrt(sum(sum((RFPredictYield-TestYield).^2))/size(TestYield,1));
RFrMatrix=corrcoef(RFPredictYield,TestYield);
RFr=RFrMatrix(1,2);
RFRMSEMatrix=[RFRMSEMatrix,RFRMSE];
RFrAllMatrix=[RFrAllMatrix,RFr];
if RFRMSE<1000
disp('RFRMSE') ;
disp(RFRMSE);
end
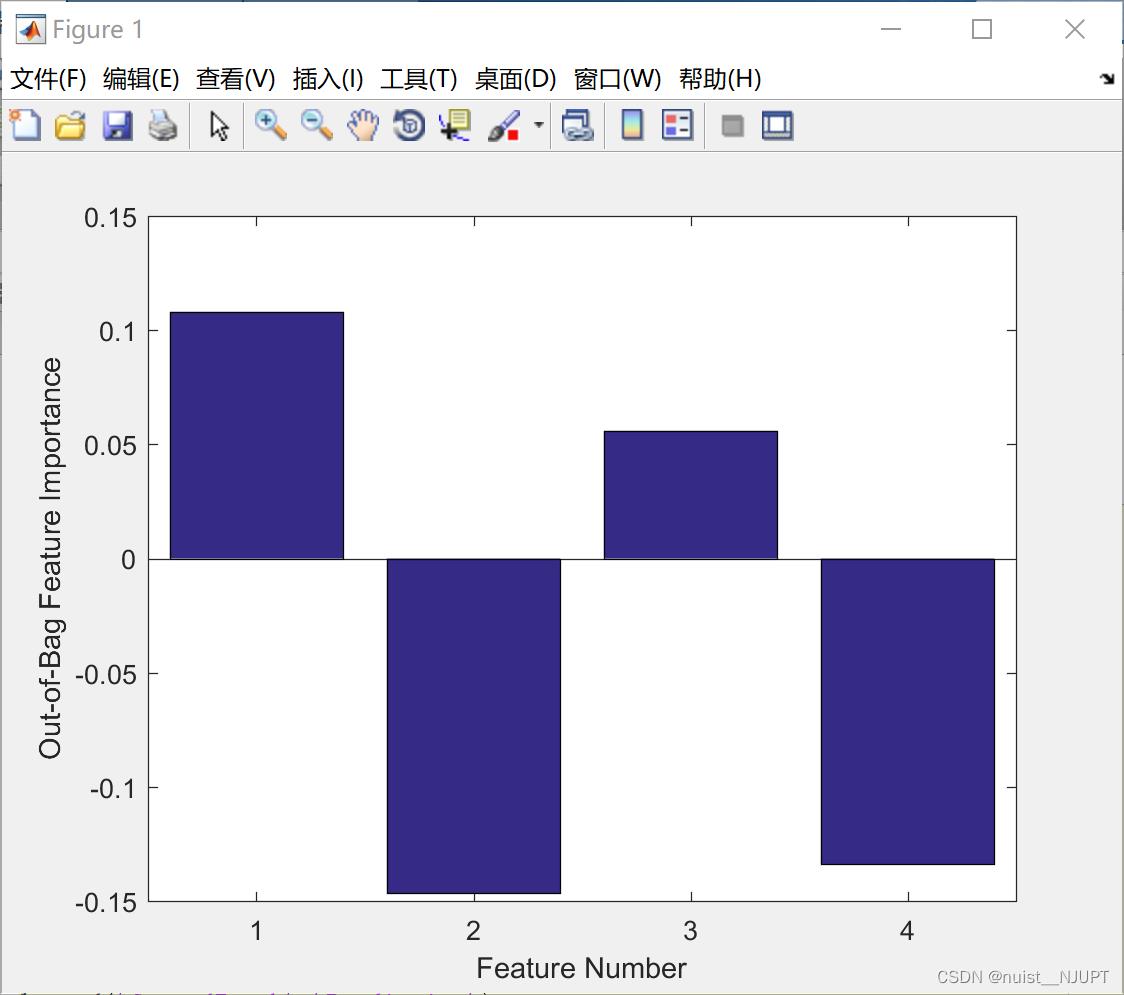
%% 比较特征的重要性
figure
bar(RFModel.OOBPermutedVarDeltaError)
xlabel('Feature Number')
ylabel('Out-of-Bag Feature Importance')
[mae,rmse,r2,mape] = EvlMetrix(TestYield,RFPredictYield)
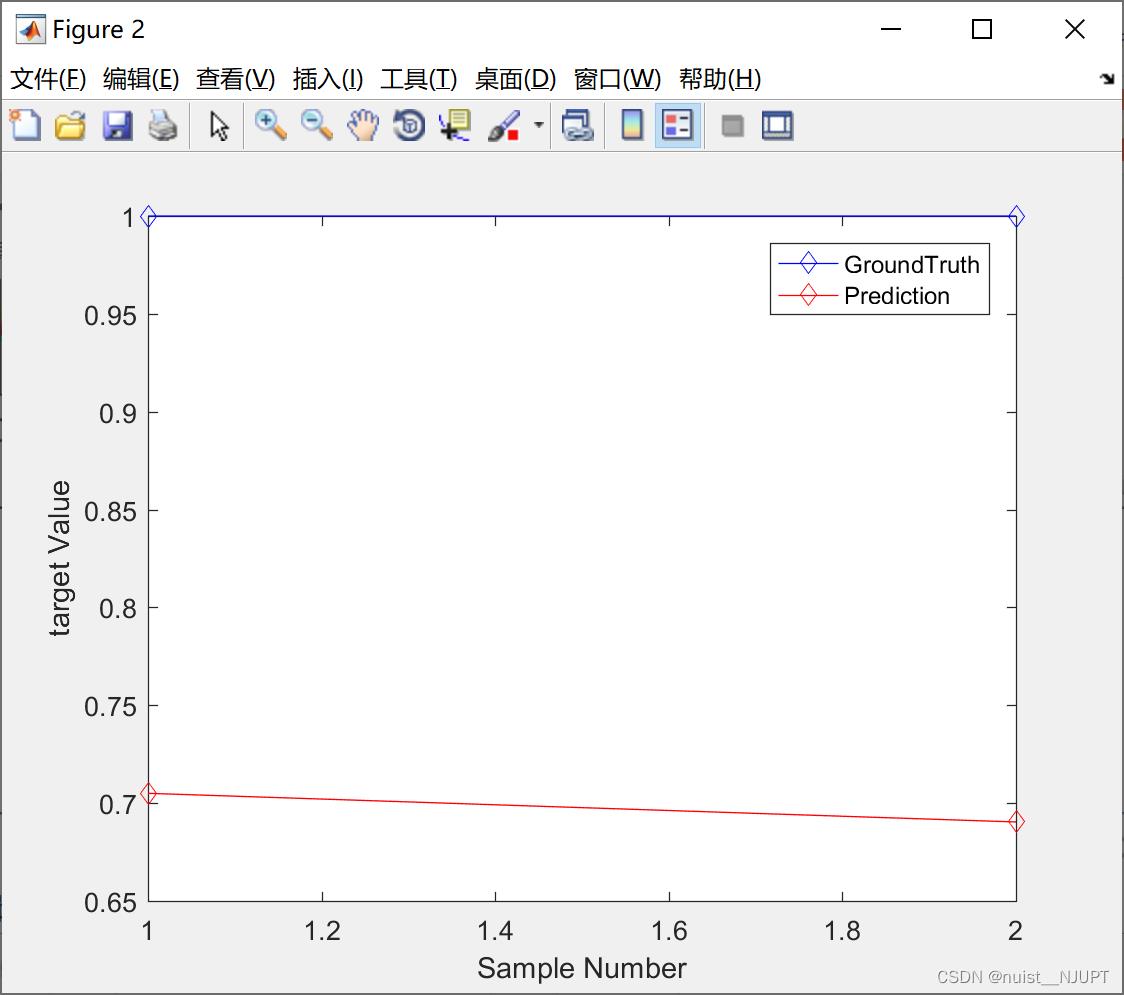
figure
plot(TestYield,'b-d')
hold on
plot(RFPredictYield,'r-d')
hold off
legend('GroundTruth','Prediction')
xlabel('Sample Number')
ylabel('target Value')
我就用了两个测试数据,效果不是特别明显。
下面的是每个特征对分类的重要性,1>3>4>2,这个数据量越大,越准确,因为我的数据量很小,所有效果不是很明显。
三、Logistic模型
3.1、Logistic模型理论
我们看一下这个二分类问题,给了一些水果的属性数据和水果名称,根据水果水果属性,对水果名称进行预测。

首先需要创建虚拟变量,我们根据水果名称创建0和1的虚拟变量,用spss如下:

对于二分类问题,我们可以考虑使用logistic模型,预测的概率决定了分类类别,如下:
 一般就是使用极大似然估计进行参数估计,然后代入公式进行预测,如下:
一般就是使用极大似然估计进行参数估计,然后代入公式进行预测,如下:


3.2、SPSS求解逻辑回归
SPSS求解逻辑回归的过程如下,选中自变量和因变量,便可以完成回归预测。
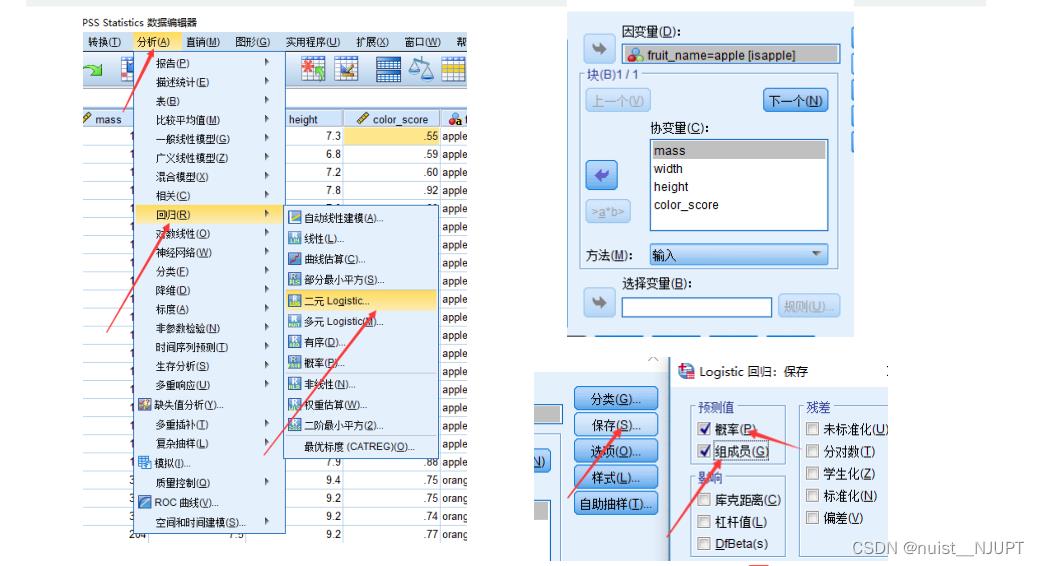
预测的结果在如下表中,第一个是预测值,第二个是预测的分类值。
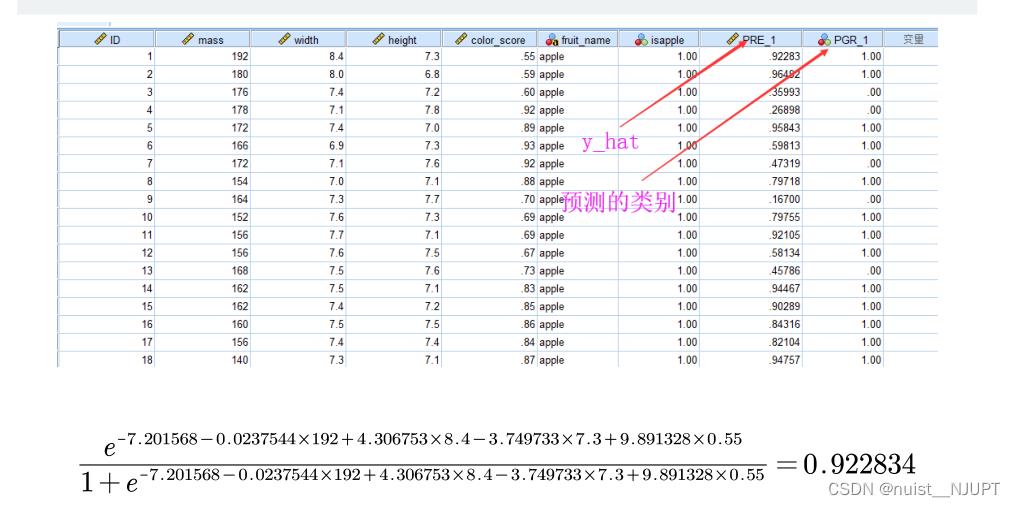
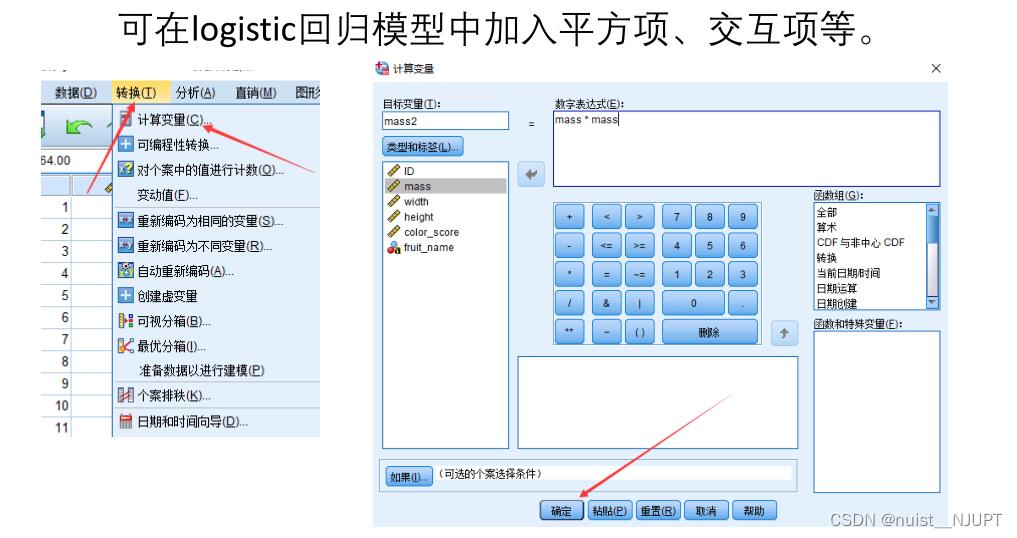
如果预测效果比较差,可以加入平方项作为自变量进行预测,一般会增加预测准确率,但是有可能造成过拟合,即训练效果好,测试效果差,泛化能力差,故可以划分训练集和测试集,多次交叉验证,得到一个稳定的结果。
以上是关于决策树(DecisionTree)和随机森林(Random Forests)的主要内容,如果未能解决你的问题,请参考以下文章